Codeforces Round #706 (Div. 2)
Codeforces Round #706 (Div. 2)
Codeforces Round #706 (Div. 2)
A Split it!
题意
给出字符串 \(S\)
询问是否存在 \(k+1\) 个非空字符串使得
\(a_1a_2a_3...a_ka_{k+1}a_k...a=S\)
题解
左右往中间扫就得了。
代码
B Max and Mex
题意
\(n\) 个数， \(k\) 次操作，每次操作添加 \(\lceil \frac {mex+max} 2\rceil\)
问最终有几种数。
题解
设 mex 为 \(a\) ，max 为 \(b\)
显然 \(a\neq b\)
当 \(a<b\) 时，\(\lceil \frac {a+b} 2\rceil>a\) 会一直添加这个数
当 \(a>b\) 时，显然集合里已经有了 \(0,1,2,3,...,b\)，接下来会添加 \(b+1\) ，循环 \(k\) 次。
代码
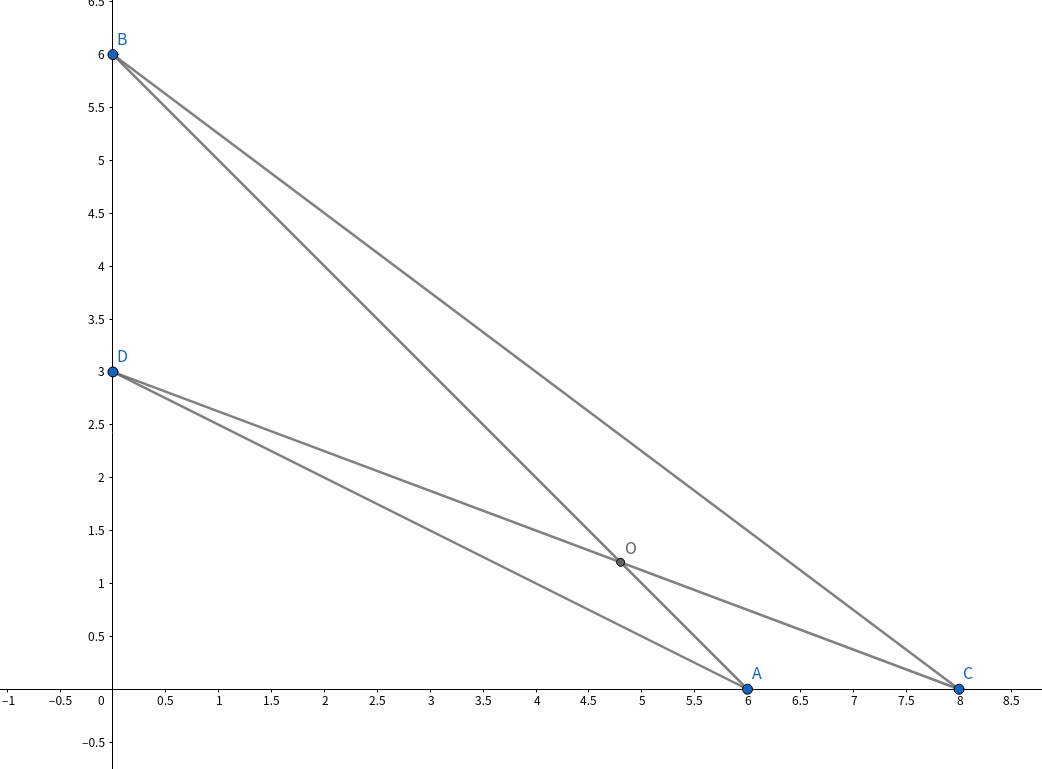
C Diamond Miner
题意
\(n\) 个矿工，坐标 \((0,y_i)\)
\(n\) 个矿产，坐标 \((x_i,0)\)
为每个矿工分配一个矿产，一个对一个，每个对答案的贡献是 \(\sqrt{x_i^2+y_i^2}\)
求答案的最小值。
题解
结论题。
将贡献转化为斜边
不妨全取 \(abs\)
如果交叉一定比不交叉的要劣（我是做的时候是举栗子的/shake)
所以对矿工和矿产排序一个对一个。
代码
D Let's Go Hiking
题面
给出一个排列。两个人 Q 和 D 玩游戏。
Q 选定初始位置 \(x\) ，D 在他之后选定初始位置 \(y\)。
之后每个人轮流操作，每个人只能向左或向右走一步。
Q 只能走数值越来越小的，D只能走数值越来越大的。
两个人不能走对方现在在的格子。
先不能动的人输。
求能使 Q 取胜的 \(x\) 数目。
题解
求最长单调序列数目。假设最长的 \(len\) 有 \(cnt\) 个序列达到时，
如果 \(cnt>2\) ，Q 走一个最长链，D 走一个最长链，先手 Q 必输。
如果 \(cnt=1\) ，Q 一开始走，D 就拦住他的下一步，Q 必输。
如果 \(cnt=2\) ，为了防止出现 \(cnt=1\) 的情况，Q一定选择两个最长链的山峰走，如果没有山峰那Q就必输。
如果有山峰，
如果 \(l\bmod 2=0\)，D选择其中一端的尾巴，Q是先手一定会输。
如果 \(l\bmod 2=1\)，D选择其中一端的尾巴，Q和它走同一端一定赢。如果D不选尾巴也不能赢。
代码
E Garden of the Sun
题意
有一个 \(n*m\) 的花田。有雷电清除了一些格子的花，现在你要主动清除一些格子的花使得所有空格子两两可达（判断是否可达时，你只可以走向有公共边的格子）。而且希望一对空格子通路只有一条。
注意：雷电清除的格子没有公共点或者公共边。
题解
多条通路的本质是环。
全部清除。显然会形成多条环。
如果隔一列清除一个也很容易形成环。
隔两列清除一列，不可能形成环，但是可能不连通。
因此要在空的两列里选择一行涂黑使得他们联通。
如果无脑清除第一行，在第二行雷电清除的花时就会暴毙。
注意到，第一行和第二行不可能同时在这两列里都有被雷电清除的花，
所以选择有雷电清除的花的一行清除光。
每一列掌管自己之前的两列。在不考虑时自动掌管左右两列。
为了防止最后几列出问题。
在 \(m\bmod 3=0\) 时，每3列一组清除中间列。
在 \(m\bmod 3=1\) 时，每3列一组清除第一列。
在 \(m\bmod 3=2\) 时，上面两种随便哪个都行。
代码
F BFS Trees
什么破题面 中考英语完蛋了
题意
我们管一张图的生成树叫a BFS tree rooted at 点 \(s\) ，当且仅当对于任意的点 \(t\)，在图上 \((s,t)\) 的最短路长度与在生成树上 \((s,t)\) 的距离相等。
给出一张图，定义 \(f(x,y)\) 是同时 rooted at 点 \(x\) 和点 \(y\) 的 BFS tree 数目。
给出一张 \(n\) 点 \(m\) 边的无边权无向图，计算对于所有 \((i,j)\) 的 \(f(i,j)\) 并输出。
题解
计算 \(f(i,j)\)
求出 \(dis[i][j]\)
如果 \(dis[i][k]+dis[k][j]-1=dis[i][j]\) ，则 \(k\) 在 \(i\) 到 \(j\) 的最短路上。
如果 \(k>dis[i][j]\)，那肯定有多条最短路，感性理解一下拼起来变成图不可能是树了。\(i,j\) 两位意见不统一了。
然后，考虑其他顶点 \(i\) 的贡献，在 \(x\) 和 \(y\) 的bfs树中，有且仅有一条连接 \(i\) 和 \(j\) 的边， \(j\) 满足 \(dist(x,i)=dist(x，j)+1\ \and \ dist(y，i)=dist(y，j)+1\)。（选定 \(j\) 是父亲）
