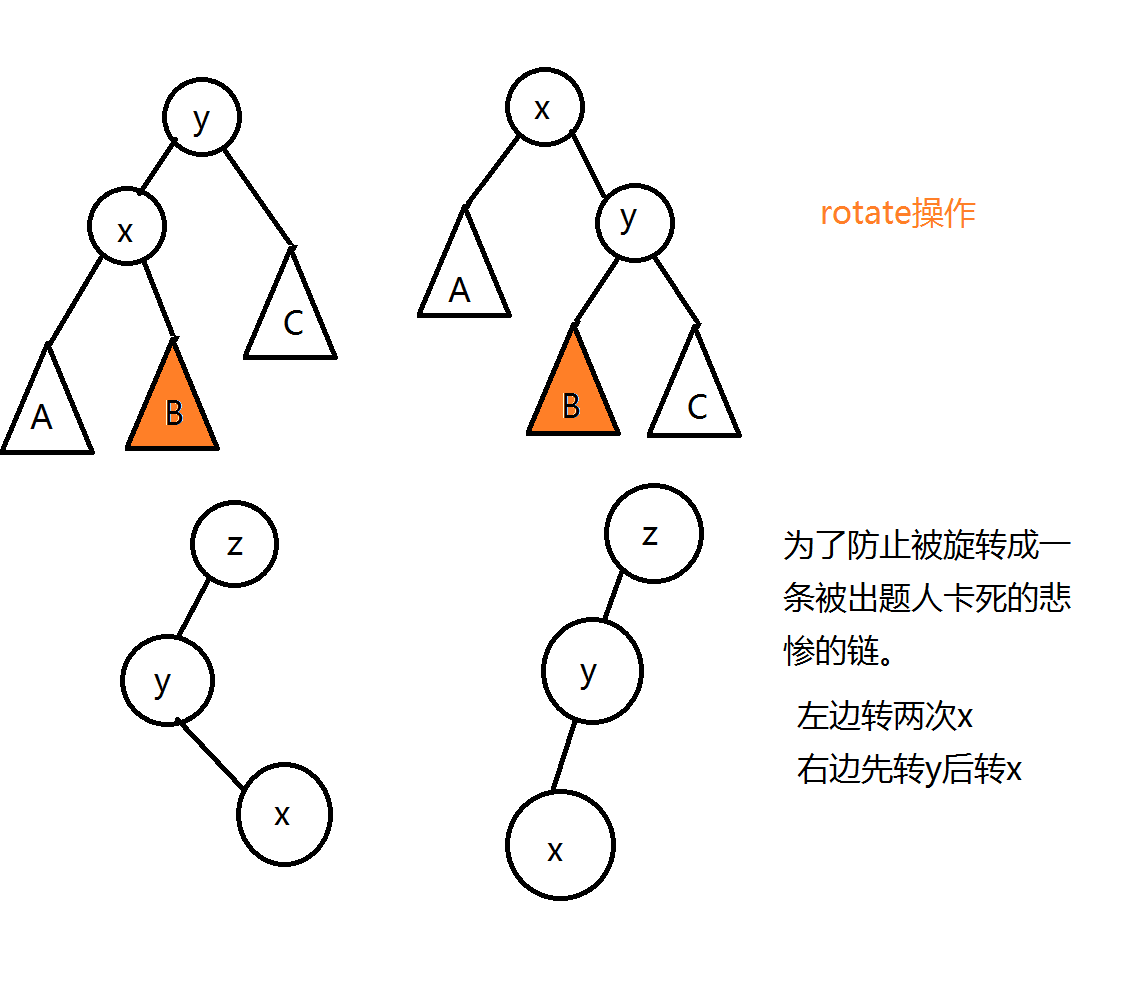
关于平衡树
平衡树白痴,学了忘忘了学,平均比人晚两年
Splay
b-x断 b-y成;x-y断 y-x成;y-fa[y]断 x-fa[y]成
主要是双旋操作。
之字型一眼就能看出来没问题。
双旋的优越性在一字型层数>4时才会体现
接下来这个图是我赫的
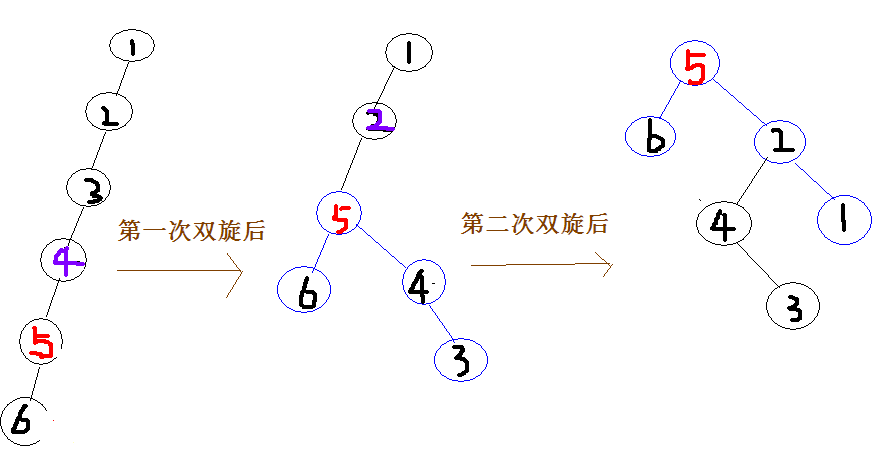
上图所说的
void rotate(int x){
int y=tr[x].fa,z=tr[y].fa,k=(tr[y].ch[1]==x);
tr[z].ch[(tr[z].ch[1]==y)]=x; tr[x].fa=z;
tr[y].ch[k]=tr[x].ch[k^1]; tr[tr[x].ch[k^1]].fa=y;
tr[x].ch[k^1]=y; tr[y].fa=x;
update(y); update(x);
return;
}
void splay(int x,int goal){
// cout<<x<<" "<<goal<<endl;
while(tr[x].fa!=goal){
int y=tr[x].fa,z=tr[y].fa;
if(z!=goal)
((tr[z].ch[0]==y)^(tr[y].ch[0]==x))?rotate(x):rotate(y);
rotate(x);
}
if(goal==0) rt=x;
return;
}
接下来:
insert:按二叉检索树找找到那个位置然后更新,再splay保持平衡。
delete:把x的前继splay到根,后继splay到右儿子,更新右儿子的左儿子,再splay保持平衡。
find:找到val=x的节点并把它splay到根。
rk:find(x) 然后左节点的点的个数,注意因为之前加入了 -inf 所以不用+1
kth:之前加入了-inf,所以查找的是第 x+1 个。特判一下不可能找到的情况其他往下找就是了。
前继后继:find(x) 之后,前继:在左儿子里找永远右的;后继:在右儿子里找永远左的。
没事别忘splay
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mkp make_pair
#define pb push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
#define fi first
#define se second
const int N = 1e5 + 10, inf = 0x3f3f3f3f;
int tot, rt;
struct node {
int fa, val, ch[2], cnt, sz;
node() {
fa = val = ch[0] = ch[1] = cnt = sz = 0;
}
}tr[N];
void update(int x) {
tr[x].sz = tr[tr[x].ch[0]].sz + tr[tr[x].ch[1]].sz + tr[x].cnt;
}
void rotate(int x) {
int y = tr[x].fa, z = tr[y].fa, k = (tr[y].ch[1] == x);
tr[z].ch[tr[z].ch[1] == y] = x; tr[x].fa = z;
tr[y].ch[k] = tr[x].ch[k ^ 1]; tr[tr[y].ch[k]].fa = y;
tr[x].ch[k ^ 1] = y; tr[y].fa = x;
update(y); update(x);
}
void splay(int x, int goal) {
while(tr[x].fa != goal) {
int y = tr[x].fa, z = tr[y].fa;
if(z != goal) {
((tr[y].ch[1] == x) ^ (tr[z].ch[1] == y)) ? rotate(y) : rotate(x);
rotate(x);
} else rotate(x);
}
if(goal == 0) rt = x;
}
int newnode(int fa, int val) {
++tot;
tr[fa].ch[val > tr[fa].val] = tot;
tr[tot].fa = fa; tr[tot].val = val;
tr[tot].ch[0] = tr[tot].ch[1] = 0;
tr[tot].cnt = tr[tot].sz = 1;
return tot;
}
void find(int val) {
int nw = rt;
while(tr[nw].ch[val > tr[nw].val] && tr[nw].val != val)
nw = tr[nw].ch[val > tr[nw].val];
splay(nw, 0);
}
int nxt(int val, int tp) {
find(val);
int nw = rt;
if(tr[nw].val < val && !tp) return nw;
if(tr[nw].val > val && tp) return nw;
nw = tr[nw].ch[tp]; while(tr[nw].ch[tp ^ 1]) nw = tr[nw].ch[tp ^ 1];
return nw;
}
void ins(int val) {
int nw = rt, fa = 0;
while(tr[nw].val != val && nw)
fa = nw, nw = tr[nw].ch[val > tr[nw].val];
if(nw) tr[nw].cnt++, tr[nw].sz++;
else nw = newnode(fa, val);
splay(nw, 0);
}
void del(int val) {
int x = nxt(val, 0), y = nxt(val, 1);
splay(x, 0); splay(y, x);
int nw = tr[y].ch[0];
if(tr[nw].cnt > 1) tr[nw].cnt--, tr[nw].sz--, splay(nw, 0);
else tr[y].ch[0] = 0, splay(y, 0);
}
int rk(int val) {
find(val); return tr[tr[rt].ch[0]].sz;
}
int kth(int nw, int k) {
k++; if(tr[nw].sz < k) return 0;
while(nw) {
int l = tr[nw].ch[0], r = tr[nw].ch[1];
if(tr[l].sz >= k) { nw = l; continue; }
k -= tr[l].sz; if(tr[nw].cnt >= k) return nw;
k -= tr[nw].cnt; nw = r;
}
return nw;
}
int main(){
// freopen("ex.in", "r", stdin);
// freopen("ex.out", "w", stdout);
ins(-inf); ins(inf);
int n; scanf("%d", &n);
while(n--) {
int op, x; scanf("%d%d", &op, &x);
//cout<<"*"<<op<<" "<<x<<endl;
if(op == 1) ins(x);
else if(op == 2) del(x);
else if(op == 3) printf("%d\n", rk(x));
else if(op == 4) printf("%d\n", tr[kth(rt, x)].val);
else printf("%d\n", tr[nxt(x, (op == 5 ? 0 : 1))].val);
}
return 0;
}
//你就不知道cnt变了sz也会变吗,啊?
就这?就这?就这?就这破玩意折腾了我两年??
文艺平衡树:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mkp make_pair
#define pb push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
#define fi first
#define se second
const int N = 1e5 + 10, inf = 0x3f3f3f3f;
int n, tot, rt;
struct node {
int fa, val, ch[2], cnt, sz, lz;
node() {
fa = val = ch[0] = ch[1] = cnt = sz = lz = 0;
}
}tr[N];
void pushdown(int x) {
if(tr[x].lz) {
int l = tr[x].ch[0], r = tr[x].ch[1];
tr[l].lz ^= 1; tr[r].lz ^= 1;
swap(tr[x].ch[0], tr[x].ch[1]);
tr[x].lz = 0;
}
}
void update(int x) {
tr[x].sz = tr[tr[x].ch[0]].sz + tr[tr[x].ch[1]].sz + tr[x].cnt;
}
void rotate(int x) {
int y = tr[x].fa, z = tr[y].fa;
pushdown(y); pushdown(x);
int k = (tr[y].ch[1] == x);
tr[z].ch[tr[z].ch[1] == y] = x; tr[x].fa = z;
tr[y].ch[k] = tr[x].ch[k ^ 1]; tr[tr[y].ch[k]].fa = y;
tr[x].ch[k ^ 1] = y; tr[y].fa = x;
update(y); update(x);
}
void splay(int x, int goal) {
while(tr[x].fa != goal) {
int y = tr[x].fa, z = tr[y].fa;
if(z != goal) {
((tr[y].ch[1] == x) ^ (tr[z].ch[1] == y)) ? rotate(y) : rotate(x);
rotate(x);
} else rotate(x);
}
if(goal == 0) rt = x;
}
int newnode(int fa, int val) {
++tot;
tr[fa].ch[val > tr[fa].val] = tot;
tr[tot].fa = fa; tr[tot].val = val;
tr[tot].ch[0] = tr[tot].ch[1] = 0;
tr[tot].cnt = tr[tot].sz = 1;
return tot;
}
void ins(int val) {
int nw = rt, fa = 0;
while(tr[nw].val != val && nw)
fa = nw, nw = tr[nw].ch[val > tr[nw].val];
if(nw) tr[nw].cnt++, tr[nw].sz++;
else nw = newnode(fa, val);
splay(nw, 0);
}
int kth(int nw, int k) {
k++; if(tr[nw].sz < k) return 0;
while(nw) {
pushdown(nw);
int l = tr[nw].ch[0], r = tr[nw].ch[1];
if(tr[l].sz >= k) { nw = l; continue; }
k -= tr[l].sz; if(tr[nw].cnt >= k) return nw;
k -= tr[nw].cnt; nw = r;
}
return nw;
}
void dfs(int u) {
pushdown(u);
if(tr[u].ch[0]) dfs(tr[u].ch[0]);
if(tr[u].val >= 1 && tr[u].val <= n) printf("%d ", tr[u].val);
if(tr[u].ch[1]) dfs(tr[u].ch[1]);
update(u);
}
void work(int l, int r) {
int x = kth(rt, r + 1); int y = kth(rt, l - 1);
splay(x, 0); splay(y, x);
int nw = tr[y].ch[1];
tr[nw].lz ^= 1;
splay(nw, 0);
}
int main(){
// freopen("ex.in", "r", stdin);
// freopen("ex.out", "w", stdout);
ins(-inf); ins(inf);
int m; scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) ins(i);
while(m--) { int l, r; scanf("%d%d", &l, &r); work(l, r); }
dfs(rt); puts("");
return 0;
}
FHQ-treap
两个基础操作。
Split
把一个treap裂成两个。
两种类型。
- 按照权值。将权值\(\le k\) 的节点分到一棵树里。
- 按照排名。将前 \(k\) 个分到一棵树里。
这里采用按照权值分裂的。才不是因为我以前按照排名分配的调了一天也调不出来
void split(int now,int k,int &x,int &y)
{
if (!now) x=y=0;
else
{
if (val[now]<=k) x=now,split(ch[now][1],k,ch[now][1],y);
else y=now,split(ch[now][0],k,x,ch[now][0]);
update(now);
}
}
对于我们遍历到的每一个点,
-
假如它的权值小于等于 \(k\),那么它的所有左子树,都要分到左边的树里,然后遍历它的右儿子。
-
假如大于k,把它的所有右子树分到右边的树里,遍历左儿子。
因为它的最多操作次数就是一直分到底,效率就是 \(O(\log n)\) 。
按照排名分裂的。有点像找第 \(k\) 大。
void split(int now,int k,int &x,int &y)
{
if (!now) x=y=0;
else
{
if (k<=siz[ch[now][0]]) y=now,split(ch[now][0],k,x,ch[now][0]);
else x=now,split(ch[now][1],k-siz[ch[now][0]]-1,ch[now][1],y);
update(now);
}
}
Merge
把两个treap合在一起。保证第一个权值小于第二个。
因为第一个Treap的权值都比较小,我们比较一下它的tar(附加权值),
-
假如第一个的tar小,我们就可以直接保留它的所有左子树,接着把第一个Treap变成它的右儿子。
-
反之,我们可以保留第二棵的所有右子树,指针指向左儿子。
你可以把这个过程形象的理解为在第一个Treap的左子树上插入第二个树,也可以理解为在第二个树的左子树上插入第一棵树。
因为第一棵树都满足小于第二个树,所以就变成了比较tar来确定树的形态。
也就是说,我们其实是遍历了第一个trep的根->最大节点,第二个Treap的根->最小节点,也就是 \(O(\log n)\)
int merge(int x,int y)
{
if (!x || !y) return x+y;
if (pri[x]<pri[y])
{
ch[x][1]=merge(ch[x][1],y);
update(x);
return x;
}
else
{
ch[y][0]=merge(x,ch[y][0]);
update(y);
return y;
}
}
insert
把treap按v分裂成x和y,然后合并 \((x,newnode(v))\) ,再合并 \((x,y)\)
void ins(int v){
int x,y;
split(rt,v,x,y);
rt=merge(merge(x,newnode(v)),y);
return;
}
delete
把treap按v分裂成x和z,
再将x按v-1分裂成x和y。
y是两个儿子合并。
x再和y合并。
x再和z合并。
void del(int v){
int x,y,z;
split(rt,v,x,z);
split(x,v-1,x,y);
y=merge(tr[y].ch[0],tr[y].ch[1]);
rt=merge(merge(x,y),z);
return;
}
precursor
前驱 按v-1分裂成x,y,在x里找最大值
successor
后继 按v分裂成x,y,在y里找最小值
rank
按 v-1 分裂,排名是 x 的 sz。
kth
正常在二叉检索树上找。
操作区间
我们先把root的前r个split出来,再在前面的子树中split前l-1个,然后我们就得到了操作区间
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mkp make_pair
#define pb push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
#define fi first
#define se second
const int N = 1e5 + 10;
int tot, rt;
struct node {
int val, pri;
int ch[2];
int cnt, sz;
}tr[N];
void update(int x) {
tr[x].sz = tr[tr[x].ch[0]].sz + tr[tr[x].ch[1]].sz + tr[x].cnt;
}
int newnode(int val) {
++tot;
tr[tot].val = val;
tr[tot].pri = rand();
tr[tot].ch[0] = tr[tot].ch[1] = 0;
tr[tot].cnt = tr[tot].sz = 1;
return tot;
}
void split(int nw, int val, int &x, int &y) {
if(!nw) { x = y = 0; return; }
if(tr[nw].val <= val) x = nw, split(tr[nw].ch[1], val, tr[nw].ch[1], y);
else y = nw, split(tr[nw].ch[0], val, x, tr[nw].ch[0]);
update(nw);
}
int merge(int x, int y) {
if(!x || !y) return x + y;
if(tr[x].pri < tr[y].pri) {
tr[x].ch[1] = merge(tr[x].ch[1], y);
update(x); return x;
} else {
tr[y].ch[0] = merge(x, tr[y].ch[0]);
update(y); return y;
}
}
void ins(int val) {
int x, y, z;
split(rt, val, x, z);
split(x, val - 1, x, y);
if(y) tr[y].cnt++, tr[y].sz++; else y = newnode(val);
rt = merge(merge(x, y), z);
return;
}
void del(int val) {
int x, y, z;
split(rt, val, x, z); split(x, val - 1, x, y);
tr[y].cnt--; tr[y].sz--;
if(tr[y].cnt == 0) y = merge(tr[y].ch[0], tr[y].ch[1]);
rt = merge(merge(x, y), z);
}
int kth(int nw, int k) {
if(tr[nw].sz < k) return 0;
while(nw) {
int l = tr[nw].ch[0], r = tr[nw].ch[1];
if(tr[l].sz >= k) { nw = l; continue; }
k -= tr[l].sz; if(tr[nw].cnt >= k) return nw;
k -= tr[nw].cnt; nw = r;
}
return nw;
}
int rk(int val) {
int x, y, ret = 0;
split(rt, val - 1, x, y);
ret = tr[x].sz + 1;
rt = merge(x, y);
return ret;
}
int nxt(int val, int tp) {
//cout<<"nxt: "<<val<<" "<<tp<<endl;
int x, y, ret = 0;
if(tp == 0) {
split(rt, val - 1, x, y);
ret = kth(x, tr[x].sz);
} else {
split(rt, val, x, y);
ret = kth(y, 1);
}
rt = merge(x, y);
return ret;
}
int main(){
// freopen("ex.in", "r", stdin);
// freopen("ex.out", "w", stdout);
srand(time(0));
int n; scanf("%d", &n);
while(n--) {
int op, x; scanf("%d%d", &op, &x);
//cout<<"*"<<op<<" "<<x<<endl;
if(op == 1) ins(x);
else if(op == 2) del(x);
else if(op == 3) printf("%d\n", rk(x));
else if(op == 4) printf("%d\n", tr[kth(rt, x)].val);
else printf("%d\n", tr[nxt(x, (op == 5 ? 0 : 1))].val);
}
return 0;
}
//你就不知道cnt变了sz也会变吗,啊?
文艺平衡树:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mkp make_pair
#define pb push_back
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
#define fi first
#define se second
const int N = 1e5 + 10;
int tot, rt;
struct node {
int val, pri;
int ch[2];
int cnt, sz;
int lz;
}tr[N];
void pushdown(int x) {
if(tr[x].lz) {
int l = tr[x].ch[0], r = tr[x].ch[1];
tr[l].lz ^= 1; tr[r].lz ^= 1;
swap(tr[x].ch[0], tr[x].ch[1]);
tr[x].lz = 0;
}
}
void update(int x) {
tr[x].sz = tr[tr[x].ch[0]].sz + tr[tr[x].ch[1]].sz + tr[x].cnt;
}
int newnode(int val) {
++tot;
tr[tot].val = val;
tr[tot].pri = rand();
tr[tot].ch[0] = tr[tot].ch[1] = 0;
tr[tot].cnt = tr[tot].sz = 1;
tr[tot].lz = 0;
return tot;
}
void split(int nw, int k, int &x, int &y) {
if(!nw) { x = y = 0; return; }
pushdown(nw);
int l = tr[nw].ch[0], r = tr[nw].ch[1];
if(tr[l].sz + tr[nw].cnt <= k) x = nw, split(r, k - tr[l].sz - tr[nw].cnt, tr[nw].ch[1], y);
else y = nw, split(l, k, x, tr[nw].ch[0]);
update(nw);
}
int merge(int x, int y) {
if(!x || !y) return x + y;
if(tr[x].pri < tr[y].pri) {
pushdown(x);
tr[x].ch[1] = merge(tr[x].ch[1], y);
update(x); return x;
} else {
pushdown(y);
tr[y].ch[0] = merge(x, tr[y].ch[0]);
update(y); return y;
}
}
void work(int l, int r) {
int x, y, z; split(rt, r, x, z); split(x, l - 1, x, y);
tr[y].lz ^= 1; rt = merge(merge(x, y), z);
return;
}
void dfs(int u) {
pushdown(u);
if(tr[u].ch[0]) dfs(tr[u].ch[0]);
printf("%d ", tr[u].val);
if(tr[u].ch[1]) dfs(tr[u].ch[1]);
update(u);
}
int main(){
// freopen("ex.in", "r", stdin);
// freopen("ex.out", "w", stdout);
srand(time(0));
int n, m; scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) rt = merge(rt, newnode(i));
while(m--) { int l, r; scanf("%d%d", &l, &r); work(l, r); }
dfs(rt); puts("");
return 0;
}
//你就不知道cnt变了sz也会变吗,啊?
替罪羊树
看下不平衡了就拍扁重建。
调了9个月,草。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,rot,gs;
double alpha=0.7;
double bmax(double x,double y){ return (x>y)?x:y; }
vector<int>vec;
struct scapegoat_tree{
int val[N<<1],sz[N<<1],cnt[N<<1],tl[N<<1],tr[N<<1];
void newnode(int &rt,int x,int cntx){
rt=++gs; val[rt]=x; cnt[rt]=sz[rt]=cntx;
tl[rt]=tr[rt]=0;
return;
}
void ins(int &rt,int x) {
//cout<<rt<<" "<<x<<endl;
if(!rt){ newnode(rt,x,1); return; }
if(x<val[rt]) ins(tl[rt],x);
else if(x>val[rt]) ins(tr[rt],x);
else cnt[rt]++;
sz[rt]=sz[tl[rt]]+sz[tr[rt]]+cnt[rt];
return;
}
void del(int rt,int x) {
if(x<val[rt]) del(tl[rt],x);
else if(x>val[rt]) del(tr[rt],x);
else cnt[rt]--;
sz[rt]=sz[tl[rt]]+sz[tr[rt]]+cnt[rt];
}
void dfs(int rt){
if(tl[rt]) dfs(tl[rt]);
vec.push_back(rt);
if(tr[rt]) dfs(tr[rt]);
tl[rt]=tr[rt]=0;
}
void build(int &rt,int l,int r){
if(l>r) return;
int mid=(l+r)>>1; rt=vec[mid];
build(tl[rt],l,mid-1);
build(tr[rt],mid+1,r);
sz[rt]=sz[tl[rt]]+sz[tr[rt]]+cnt[rt];
return;
}
void rebuild(int &rt) {
//中序遍历,拍扁重建。
vec.clear(); dfs(rt);
build(rt,0,(int)vec.size()-1);
}
bool isbad(int rt) {
return (alpha*sz[rt]<bmax(sz[tl[rt]],sz[tr[rt]]));
}
void blc(int &rt,int x) {
if(!rt) return;
if(isbad(rt)) rebuild(rt);
else {
if(x<val[rt]) blc(tl[rt],x);
else if(x>val[rt]) blc(tr[rt],x);
}
return;
}
int rk(int rt,int x){
int ret=1;
while(1){
// cout<<rt<<endl;
if(!rt) return ret;
if(x<val[rt]) rt=tl[rt];
else {
if(x==val[rt]) return ret + sz[tl[rt]];
else {
ret+=sz[tl[rt]]+cnt[rt]; rt=tr[rt];
}
}
}
}
int kth(int rt,int x){//x:有x-1个数比num小
if(x<=sz[tl[rt]]) return kth(tl[rt],x);
else {
if(x<=sz[tl[rt]]+cnt[rt]) return rt;
if(tr[rt]) return kth(tr[rt],x-sz[tl[rt]]-cnt[rt]);
else return rt;//?这里的锅?
}
}
int pre(int x){
//有rk(rot,x)-1个数比x小,因此他的后继有rk(rot,x)-2个数<=他。
//当x在树里,rk(rot,x)-1不包括它本身,它的前继显然排名在rk(rot,x)及之前
//当x不在树里,rk(rot,x)-1不会包括它自己。它的前继显然排名在rk(rot,x)及之前
return kth(rot,rk(rot,x)-1);
}
int nxt(int x){
//有rk(rot,x+1)-1个数比x+1小,因此他的后继有rk(rot,x)-1个数<=他。
//当x在树里,rk(rot,x+1)-1就包括了它自己。显然它的后继>=那么多数
//当x不在树里,rk(rot,x+1)-1不会包括它自己。显然它的后继>=那么多数
return kth(rot,rk(rot,x+1));
}
}tr;
int main(){
//freopen("example.in","r",stdin);
scanf("%d",&n);
for(int i=1,opt,x;i<=n;i++){
scanf("%d%d",&opt,&x);
if(opt==1) tr.ins(rot,x),tr.blc(rot,x);
if(opt==2) tr.del(rot,x),tr.blc(rot,x);
if(opt==3) printf("%d\n",tr.rk(rot,x));
if(opt==4) printf("%d\n",tr.val[tr.kth(rot,x)]);
if(opt==5) printf("%d\n",tr.val[tr.pre(x)]);
if(opt==6) printf("%d\n",tr.val[tr.nxt(x)]);
}
return 0;
}

 关于平衡树
关于平衡树