下笔春蚕食叶声。

FFT&NTT&多项式全家桶

FFT

前置芝士

多项式表示

系数表示法

\(A(x)=\sum_{i=0}^{n-1} a_i*x^i\) 表示一个 \(n-1\) 次的多项式。 计算多项式乘法复杂度为 \(O(n^2)\)

点值表示法

\(n\) 个互不相同的 \(x_i\) 带入得到 \(n\) 个$ y_i=\sum_{j=0}^{n-1} a_j*{x_i}^j$

用 \(n\) 个点\((x_1,y_1)...(x_n,y_n)\)表示一个 \(n-1\) 次多项式

复数

定义

模长: \(\sqrt{x^2+y^2}\)

幅角：从 \(x\) 轴正半轴到向量的转角的有向角

运算原则

  • 加法

    平行四边形法则

  • 乘法：

    几何：模长相乘，幅角相加

    代数： \((a+bi)*(c+di)=ac-bd+(bc+ad)i\)

单位根

定义

\(n\) 为 2 的正整数幂。

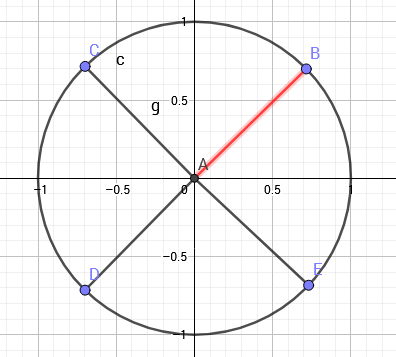
复平面上的单位圆，以原点为起点，圆的 \(n\) 等分点为终点，做\(n\) 个向量。

设幅角为正且最小的向量对应的复数为 \(\omega_n\) ，称为 \(n\) 次单位根。

其余 \(n-1\) 个复数为 \({\omega_n}^2,{\omega_n}^3...{\omega_n}^n\)

另外，在代数中，若 \(z^n=1\)，我们把 \(z\) 称为 \(n\) 次单位根。

单位根的性质
  • \({\omega_n}^k=\cos {k {\frac {2\pi} n}}+i \sin {k {\frac {2\pi} n}}\) 欧拉公式
  • \({\omega_{2n}}^{2k}={\omega_n}^k\)
  • \({\omega_n}^{k+\frac n 2}=-{\omega_n}^k\)
  • \({\omega_n}^0={\omega_n}^n=1\)

几何意义显然。

快速傅里叶变换

用点值表示法直接狂做，仍然是 \(O(n^2)\) 的，没有意义。

设多项式 \(A(x)\) 系数为 \((a_0,a_1,a_2,...a_{n-1})\)

\[A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1} \]

将其下标奇偶分类

\[A(x)=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+ (a_1x+a_3x^3+...+a_{n-1}x^{n-1}) \]

设

\[A_1(x)=a_0+a_2x+...+a_{n-2}x^{\frac n 2-1}\\ A_2(x)=a_1+a_3x+...+a_{n-1}x^{\frac n 2-1} \]

则

\[A(x)=A1(x^2)+xA_2(x^2) \]

利用单位根的性质

考虑用单位根作为 \(x\)

将 \({\omega_n}^k(k<\frac n 2)\) 带入得

\[A({\omega_n}^k)=A1({\omega_n}^{2k})+{\omega_n}^kA_2({\omega_n}^{2k})\\ =A_1({\omega_{\frac n 2}}^{k})+{\omega_n}^kA_2({\omega_{\frac n 2}}^{k}) \]

将 \({\omega_n}^{k+\frac n 2}\) 带入得

\[A(\omega_n^{k+\frac{n}{2}})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}(\omega_n^{2k+n})\\ =A_1(\omega_n^{2k})+\omega_n^{k+\frac{n}{2}}(\omega_n^{2k})\\ =A_1({\omega_{\frac n 2}}^{k})-{\omega_n}^kA_2({\omega_{\frac n 2}}^{k}) \]

这两个柿子只有一个符号不同。

前一个\(k\in[0,\frac n 2)\) ，后一个 \((k+\frac n 2) \in [\frac n 2,n)\)

计算前一个时就可以同时计算后一个。

时间复杂度 \(O(n\log n)\)

快速傅里叶逆变换

用于将点值表示法转化为系数表示法。

设 \((a_0,a_1,...,a_n)\) 的傅里叶变换（点值表示法）为 \((w_n^i,y_i)\)

设多项式 \(B(x)=\sum_{i=0}^{n-1} y_ix^i\) 的点值表示法是 \(({\omega_{n}}^{-i},c_i)\)

那么我们有

\[\begin{aligned} c_k&=\sum_{i=0}^{n-1} y_i({\omega_n}^{-k})^i\\ &=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} a_j{x_i}^j)({\omega_n}^{-k})^i\\ &=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} a_j{{(\omega_n}^i)}^j)({\omega_n}^{-k})^i\\ &=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} a_j{{(\omega_n}^i)}^j({\omega_n}^{-k})^i)\\ &=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} a_j{{(\omega_n}^j)}^i({\omega_n}^{-k})^i)\\ &=\sum_{j=0}^{n-1} a_j \sum_{i=0}^{n-1} {{(\omega_n}^{j-k})}^i\\ \end{aligned} \]

令 \(S(x)=\sum_{i=0}^{n-1} x_i\)

\[S(\omega_n^k)=\sum_{i=0}^{n-1} {({\omega_n}^k)}^i \]

等比数列求和之后

  • \(k=0\) , \(s=n\)
  • \(k\neq 0\) , \(s=0\)

考虑之前的柿子。

\[c_k=\sum_{j=0}^{n-1} a_j \sum_{i=0}^{n-1} {{(\omega_n}^{j-k})}^i\\ \]

  • \(j=k\) 时，为 \(n\)

  • \(j\neq k\) 时，为 \(0\)
    （建议直接几何意义）

所以 \(c_k=na_k\)

\[a_k=\frac {c_k} n \]

总结

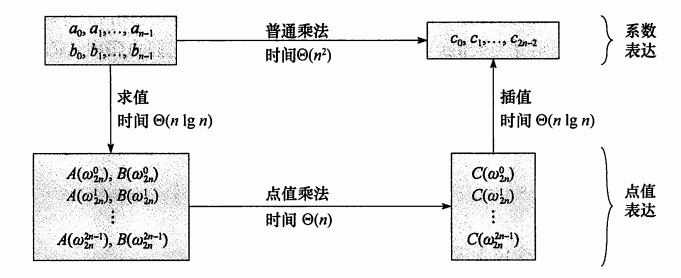
代码实现

  • 尽量手写虚数

  • 递归版

    #include<bits/stdc++.h>
using namespace std;
const int N=1e7+10;
int n,m;
double pi=acos(-1);
struct cplx{
    double x,y;
    cplx(double xx=0,double yy=0){x=xx;y=yy;}
}f[N],g[N];
cplx operator + (cplx a,cplx b){ return cplx(a.x+b.x,a.y+b.y);}
cplx operator - (cplx a,cplx b) {return cplx(a.x-b.x,a.y-b.y);}
cplx operator * (cplx a,cplx b) {return cplx(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
void fft(int lim,cplx *a,int tp){
    if(lim==1) return;
    cplx a1[(lim>>1)+5],a2[(lim>>1)+5];
    for(int i=0;i<=lim;i+=2) a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    fft(lim>>1,a1,tp);fft(lim>>1,a2,tp);
    cplx tmp=cplx(cos(2*pi/lim),tp*sin(2*pi/lim)),bg=cplx(1,0);
    for(int i=0;i<(lim>>1);i++,bg=bg*tmp){
        a[i]=a1[i]+bg*a2[i];
        a[i+(lim>>1)]=a1[i]-bg*a2[i];
    }
    return;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++) scanf("%lf",&f[i].x);
    for(int i=0;i<=m;i++) scanf("%lf",&g[i].x);
    int limit=1;while(limit<=n+m) limit<<=1;
    fft(limit,f,1);fft(limit,g,1);
    for(int i=0;i<=limit;i++) f[i]=f[i]*g[i];
    fft(limit,f,-1);
    for(int i=0;i<=m+n;i++) printf("%d ",(int)(f[i].x/limit+0.5) );
    return 0;
}

  • 迭代实现

    需要求的序列实际是原序列下标的二进制反转。

    因此对序列按照下标的奇偶性分类的过程其实是没有必要的。

    #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4e6+10;
double pi=acos(-1.0);
int n,m,id[N];
struct cplx{
    double x,y;
    cplx(double xx=0,double yy=0){ x=xx; y=yy; }
}f[N],g[N];
cplx operator + (cplx a,cplx b) { return cplx(a.x+b.x,a.y+b.y); }
cplx operator - (cplx a,cplx b) { return cplx(a.x-b.x,a.y-b.y); }
cplx operator * (cplx a,cplx b) { return cplx(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x); }
void FFT(int lim,cplx *a,int tp){
    for(int i=0;i<lim;i++) if(id[i]>i) swap(a[i],a[id[i]]);
    for(int mid=1;mid<lim;mid<<=1){
        cplx wn(cos(pi/mid),tp*sin(pi/mid));
        for(int j=0,len=mid<<1;j<lim;j+=len){
            cplx w(1,0);
            for(int k=0;k<mid;k++,w=w*wn){
                cplx x=a[j+k],y=w*a[j+k+mid];
                a[j+k]=x+y; a[j+k+mid]=x-y;
            }
        }
    }
    return;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++) scanf("%lf",&f[i].x);
    for(int i=0;i<=m;i++) scanf("%lf",&g[i].x);
    int lim=1,len=0; while(lim<=n+m) lim<<=1,len++;
    for(int i=0;i<lim;i++) id[i]=(id[i>>1]>>1)|((i&1)<<(len-1));
    FFT(lim,f,1); FFT(lim,g,1);
    for(int i=0;i<=lim;i++) f[i]=f[i]*g[i];
    FFT(lim,f,-1);
    for(int i=0;i<=n+m;i++)
        printf("%d ",(int)(f[i].x/lim+0.5));
    puts("");
    return 0;
}

    如果你是一个背板子带师，你需要记住：

    • \({\omega_n}^k=\cos {k {\frac {2\pi} n}}+i \sin {k {\frac {2\pi} n}}\)

    • \(A({\omega_n}^k)=A_1({\omega_{\frac n 2}}^{k})+{\omega_n}^kA_2({\omega_{\frac n 2}}^{k})\)

    • \(A({\omega_n}^{k+\frac n 2})=A_1({\omega_{\frac n 2}}^{k})-{\omega_n}^kA_2({\omega_{\frac n 2}}^{k})\)

    • \(a_k=\frac {c_k} n\)

NTT

可以解决FFT精度过低的问题。

原根

定义

考虑一个质数 \(p\) ，定义其原根 \(g\) 为使得 \(g^i(0\le i\le p-2)\) 互不相同的数。

为了满足单位根的四条性质，\(n\) 要是 \(p-1\) 的因数才能满足条件，\(n\) 是 2 的幂，所以 \(p\) 是形如 \(q·2^k+1\) 的质数。

http://blog.miskcoo.com/2014/07/fft-prime-table

常见模数998244353,1004535809,46976204，这些原根都是3

性质

FFT依赖了单位根的四条性质，原根都满足。

令 \({t_n}^n\equiv 1 \bmod p\) 即 \(t_n\equiv g^q \bmod p\)，等价与 \(\omega_n\)

  • \({\omega_n}^t\) 互不相同，保证点值表示的合法。显然满足。

  • \({\omega_{2n}}^{2k}={\omega_n}^k\) 用于分治。

    \({t_{2n}}=g^{\frac q 2}(p=\frac q 2 \times 2n+1)\)

    \({t_{2n}}^{2k}=g^{2k\frac q 2}=g^{kq}=(t_n)^k\)

  • \({\omega_{n}}^{k+\frac n 2}=-{\omega_n}^k\) ，用于分治

    由费马小定理 \({t_n}^n=g^{nq}=g^{p-1}\equiv 1 \bmod p\)

    \({t_n^{\frac n 2}}=1/-1\)

    ∵ \({t_n^{\frac n 2}}\neq {t_n^{0}}\) ∴ \({t_n^{\frac n 2}}=-1\)

    可推出 \({t_{n}}^{k+\frac n 2}={t_{n}}^{k}\times {t_n^{\frac n 2}}=-{t_n}^k\)

  • S(x) 在 \(x=0\) 时为 \(n\) 否则为 \(0\)

    等比数列一番再用性质三的结论。

求任意一个质数的原根

可以一一枚举 \(g\) 并检验。

结论：对于一个数 \(g\)，最小的满足\(g^k\equiv 1\bmod p\) 的正整数 \(k\) 一定是 \(p-1\) 的约数。

Proof

如果最小的 \(k\) 不是 \(p-1\) 的约数，

找到 \(x\) 满足 \(xk>p-1>(x-1)k\)

\[g^{xk}\equiv g^{p-1}\equiv g^{xk-(p-1)}\bmod p \\xk-(p-1)<k \]

矛盾

检验时，只要枚举 \(p-1\) 的所有约数 \(q\) ，检验 \(g^q\neq 1 \bmod p\) 即可。

代码实现

求原根

我没搞懂我是傻逼。

inline long long pow(const long long x, const long long n, const long long p) {
    long long ans = 1;
    for (long long num = x, tmp = n; tmp; tmp >>= 1, num = num * num % p) if (tmp & 1) ans = ans * num % p;
    return ans;
}

inline long long root(const long long p) {
    for (int i = 2; i <= p; i++) {
        int x = p - 1;
        bool flag = false;
        for (int k = 2; k * k <= p - 1; k++) if (x % k == 0) {
            if (pow(i, (p - 1) / k, p) == 1) {
                flag = true;
                break;
            }
            while (x % k == 0) x /= k;
        }

        if (!flag && (x == 1 || pow(i, (p - 1) / x, p) != 1)) {
            return i;
        }
    }
    throw;
}

NTT

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4e6+10,mod=998244353;
int n,m,id[N],A[N],B[N],g=3;
int power(int a,int b){
    int ret=1;
    while(b){
        if(b&1) ret=1ll*ret*a%mod;
        b>>=1;a=1ll*a*a%mod;
    }
    return ret;
}
void NTT(int lim,int *a,int tp){
    for(int i=0;i<lim;i++) if(id[i]>i) swap(a[i],a[id[i]]);
    for(int mid=1;mid<lim;mid<<=1){
        int wn=power(g,(mod-1)/(mid<<1));
        if(tp==-1) wn=power(wn,mod-2);
        for(int j=0,len=mid<<1;j<lim;j+=len){
            int w=1;
            for(int k=0;k<mid;k++,w=1ll*w*wn%mod){
                int x=a[j+k],y=1ll*w*a[j+k+mid]%mod;
                a[j+k]=(x+y)%mod; a[j+k+mid]=(x-y)%mod;
            }
        }
    }
    return;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++) scanf("%d",&A[i]);
    for(int i=0;i<=m;i++) scanf("%d",&B[i]);
    int lim=1,len=0; while(lim<=n+m) lim<<=1,len++;
    for(int i=0;i<lim;i++) id[i]=(id[i>>1]>>1)|((i&1)<<(len-1));
    NTT(lim,A,1); NTT(lim,B,1);
    for(int i=0;i<lim;i++) A[i]=1ll*A[i]*B[i]%mod;
    NTT(lim,A,-1);
    int inv=power(lim,mod-2);
    for(int i=0;i<=n+m;i++)
        printf("%d ",(int)((1ll*A[i]*inv%mod+mod)%mod));
    puts("");
    return 0;
}

更快的NTT：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ls(x) ((x)<<1)
#define rs(x) ((x)<<1|1)
#define fi first
#define se second
#define mkp make_pair
#define PII pair<int,int>
const int N = 4e6 + 10, mod = 998244353;
int power(int x, int y) {
	int ret = 1;
	while(y) {
		if(y & 1) ret = 1ll * ret * x % mod;
		y >>= 1; x = 1ll * x * x % mod;
	}
	return ret;
}
namespace poly {
	int lim, le, id[N], ivlim, pre[N];
	void init(int n, int m) {
		lim = 1; while(lim <= n + m + 2) lim <<= 1, le++;
		ivlim = power(lim, mod - 2);		
		
		id[0] = 0; for(int i = 1; i < lim; i++) id[i] = id[i >> 1] >> 1 | ((i & 1) << (le - 1));
		pre[0] = 1;
		for(int mid = 1; mid < lim; mid <<= 1) {
			int wn = power(3, (mod - 1) / (mid << 1));
			for(int j = 0, w = 1; j < mid; j++, w = 1ll * w * wn % mod)
				pre[mid + j] = w;
		}
	}
	void NTT(int *a, int tp) {
		for(int i = 0; i < lim; i++)
			if(id[i] > i) swap(a[i], a[id[i]]);
		for(int mid = 1; mid < lim; mid <<= 1) {
			for(int i = 0, len = (mid << 1); i < lim; i += len) {
				for(int j = 0; j < mid; j++) {
					int x = a[i + j], y = 1ll * pre[mid + j] * a[i + j + mid] % mod;
					a[i + j] = (x + y) % mod;
					a[i + j + mid] = (x + mod - y) % mod;
				}
			}
		}
		if(tp) {
			for(int i = 0; i < lim; i++)
				a[i] = 1ll * a[i] * ivlim % mod;
			reverse(a + 1, a + lim);
		}
		return;
	}
	void getmul(int n, int m,int *f, int *g, int *h) {
		NTT(f, 0); NTT(g, 0);
		for(int i = 0; i < lim; i++) h[i] = 1ll * f[i] * g[i] % mod;
		NTT(h, 1);
		return;
	}
}
int main() {
	int n, m;
	static int f[N], g[N], h[N];
	scanf("%d%d", &n, &m);
	for(int i = 0; i <= n; i++) scanf("%d", &f[i]);
	for(int i = 0; i <= m; i++) scanf("%d", &g[i]);
	poly::init(n, m);
	poly::getmul(n, m, f, g, h);
	for(int i = 0; i <= n + m; i++)
		printf("%d ", h[i]);
	puts("");
	return 0;
}

多项式全家桶

泰勒展开

泰勒有一个看着不顺眼的函数，比如说是 \(sin(x)\)

泰勒要制造一个图像和它很相似的多项式函数

泰勒会希望它的 \(n\) 阶导都相等

最后结果一定是

\[g(x)=a_0+a_1x+a_2x^2+...a_nx^n \]

这样的，也就是要求 \(a\)

保证初始点相同，\(g(0)=f(0)=a_0\)

\(f/g\) 求完 \(n\) 阶导的时候，只有最后一项非0，是 \(n!a_n\)

初始点也不一定是0，所以泰勒展开的结果是

\[G(x)=F(x_0)+\dfrac{F^{(1)}(x_0)}{1!}(x-x_0)+\dfrac{F^{(2)}(x_0)}{2!}(x-x_0)^2+\cdots \]

差不多这个意思，还是看 zzc 的或者 原版为好。

牛顿迭代

以多项式求逆为例。

已知 \(H(x)\) ，且 \(F(x)*H(x)\equiv 1 \bmod {x^{\lceil \frac n 2 \rceil}}\)

已知一个函数满足 \(G(F(x))\equiv 0\bmod {x^n}\) ，已知的！已知的！已知的！！！

把 \(G(F(x))\) 在 \(H(x)\) 泰勒展开

\[G(F(x))=G(H(x))+\dfrac{G'(H(x))}{1!}(F(x)-H(x))+\dfrac{G''(H(x))}{2!}(F(x)-H(x))^2+\cdots\\ \]

注意，这不是在拟合什么，G和G本来就一样，只是为了制造 \(F(x)\) 和 \(H(x)\) 之间的关系柿。。。

从第三项开始，由于 \(F(x),H(x)\) 的后 \(\frac n 2\) 项相同，所以都是0

\[G(F(x))=G(H(x))+{G'(H(x))}(F(x)-H(x)) \]

所以

\[G(H(x))+{G'(H(x))}(F(x)-H(x)) \equiv 0 \bmod {x^n}\\ F(x)=H(x)-\frac {G(H(x))} {G'(H(x))} \]

即

\[F(x)=F_0(x)-\frac {G(F_0(x))} {G'(F_0(x))} \]

每次如此，让它迅速逼近准确值。

本质上，迭代一次精度就可以翻倍。从 \(\bmod x^{\frac n 2}\) 到 \(\bmod x^n\)

然而没人说证明。

多项式求逆

目标

求满足 \(F(x)G(x)\equiv 1\bmod x^n\) 的 \(G\) ，系数对998244353取模。

求解

考虑倍增。

如果多项式 \(F\) 只有一项，那么显然 \(G_0\) 是 \(F_0\) 的逆元。若有 \(n\) 项，递归求解。

注意，以下 \(\frac n 2\) 均指 \(\lceil \frac n 2 \rceil\)，\('\) 不是求导后的结果。

假设已知

\[F(x)G'(x)\equiv 1 \bmod x^{ \frac n 2 } \]

需要求

\[F(x)G(x)\equiv 1 \bmod x^{ n } \]

显然

\[G(x)-G'(x)\equiv 0 \bmod x^{\frac n 2} \]

两边同时平方

\[G^2(x)+{G'}^2(x)-2G(x)G'(x)\equiv 0 \bmod x^{n} \]

两边同乘 \(F(x)\)

\[F(x)(G^2(x)+{G'}^2(x)-2G(x)G'(x))\equiv 0 \bmod x^{n} \]

又因为 \(F(x)G(x)\equiv 1 \bmod x^{ n }\)

所以

\[G(x)+F(x){G'}^2(x)-2G'(x)\equiv 0 \bmod x^{n} \]

移项

\[G(x) \equiv 2G'(x)-F(x){G'}^2(x) \bmod x^{n} \]

只需初始 \(G(0)=F(0)^{-1}\) 即可倍增。

时间复杂度：\(T(n)=T(\frac n 2)+O(n\log n)=O(n\log n)\)

关于reverse：思考一下同余的事

关于预处理：？？

多项式对数函数

目标

求一个 \(B(x)\equiv \ln A(x)\bmod {x^n}\)

求解

\[C(x)=\ln x\\ {\ln A(x)}'=C'(A(x))=C'(A(x))A'(x)=\frac 1 {A(x)}·A'(x)=\frac {A'(x)} {A(x)}\\ B'(x)=\ln A(x)\\ B'(x)=\frac {A'(x)} {A(x)}\\ \]

因此只要导一下+求逆+积分回来（？代码中似乎并不是积分）

多项式指数函数(exp)

目标

求 \(B(x)\) 满足 \(B(x)\equiv {e^{A(x)}}\bmod {x^n}\) 保证 \(A(0)=0\)

求解

\[\ln (B(x))=A(x)\\ \]

令 \(C(B(x))=\ln (B(x))-A(x)\) ，那么 \(C'(B(x))=\frac {1} {B(x)}\)

（ \(A(x)\) 可以当做常数量消掉。\(x\) 的改变，不会引起系数的改变。）

对其牛顿迭代。

\[B(x)=B_0(x)-\frac {C(B_0(x))} {C'(B_0(x))}\\ B(x)=B_0(x)-\frac {\ln (B_0(x))-A(x)} {\frac 1 {B_0(x)}}\\ B(x)=B_0(x)-{(\ln (B_0(x))-A(x)} ){B_0(x)}\\ B(x)={(1-\ln (B_0(x))+A(x)} ){B_0(x)}\\ \]

这里的 \(B_0(x)\) 指的是 \(\bmod\frac n 2\) 下的答案。依然递归求解即可。

多项式开根

目标

求 \(B(x)\) 使得 \(B^2(x)\equiv A(x)\bmod {x^n}\)

若有多解，请取零系数较小的作为答案。

求解

设 \(G(B(x))=B(x)^2-A(x)\)

\(G'(B(x))=2B(x)\)

对其牛顿迭代

\[\begin{aligned} B(x)&=B_0(x)-\frac {G(B_0{x})} {G'(B_0(x))}\\ &=B_0(x)-\frac {G(B_0(x))} {2B_0(x)}\\ &=\frac {{B_0}^2(x)+A(x)} {2B_0(x)}\\ &=\frac {B_0(x)} 2+\frac {A(x)} {2B_0(x)} \end{aligned} \]

改一改exp就得了

多项式快速幂

目标

求一个 \(B(x)\equiv A^k(x)\bmod {x^n}\)

解法

两边同时取 \(\ln\)

\[\ln(B(x))=\ln (A^k(x))\\ \ln(B(x))=k\ln (A(x)) \]

再把 \(\ln(B(x))\) exp回去即可。

多项式除法

目标

给定一个 \(n\) 次多项式 \(F(x)\) 和一个 \(m\) 次多项式 G(x) ，请求出多项式 \(Q(x)\) , \(R(x)\) ，满足以下条件：

  • \(Q(x)\) 次数为 \(n-m\)，$$R(x)$$ 次数小于 \(m\)
  • \(F(x) = Q(x) * G(x) + R(x)\)

所有的运算在模 998244353 意义下进行。

求解

定义 \(F_r(x)\) 为把 \(F(x)\) 系数翻转后的函数。

\[F(x)=\sum_{i=0}^n a_ix^i \]

则

\[F_r(x)=\sum_{i=0}^n a_{n-i}x^i\\ F_r(x)=x^nF(x^{-1}) \]

要满足

\[F(x) = Q(x)G(x) + R(x)\\ F(x^{-1}) = Q(x^{-1})G(x^{-1}) + R(x^{-1})\\ x^nF(x^{-1}) = x^m Q(x^{-1}) x^{n-m}G(x^{-1}) +x^n R(x^{-1})\\ F_r(x)=G_r(x)Q_r(x)+x^nR(x^{-1})\\ \]

两边同时模 \(x^{n-m+1}\)

\[F_r(x)\equiv G_r(x)Q_r(x) \bmod x^{n-m+1}\\ Q_r(x)\equiv F_r(x){G_r}^{-1}(x) \bmod x^{n-m+1} \]

可以计算出 \(Q(x)\) ，容易算出 \(R(x)\)

const int N=4e6+10,mod=998244353;
inline int Add(int x,int y){ x+=y; if(x>=mod) x-=mod; return x; }
inline int Sub(int x,int y){ x-=y; if(x<0) x+=mod; return x; }
inline int mul(int x,int y){ return 1ll*x*y%mod; }
inline int read(){ char ch; ch=getchar(); int num=0,fff=1; while(ch<'0'||ch>'9'){ if(ch=='-') fff=-1; ch=getchar(); } while(ch>='0'&&ch<='9') num=(num<<3)+(num<<1)+ch-'0',ch=getchar(); return num*fff; }
inline void write(int x){ if(x<0) putchar('-'),x=-x; if(x>=10) write(x/10); putchar(x%10+'0'); return; }
inline int power(int a,int b){ int ret=1; while(b){ if(b&1) ret=mul(ret,a); b>>=1;a=mul(a,a); } return ret; }
inline int inv(int x){ return power(x,mod-2); }
namespace poly{
    int len,lim,id[N],pre[N],G=3,invG=332748118;
    inline void getlim(int x){ len=0,lim=1; while(lim<x) lim<<=1,len++; }
    inline void initid(){ for(int i=0;i<lim;i++) id[i]=(id[i>>1]>>1)|((i&1)<<(len-1)); }
    void initpre(){
        for(int i=1;i<lim;i<<=1){
            int w=power(3,(mod-1)/(i<<1)); pre[i]=1;
            for(int j=1;j<i;j++) pre[i+j]=mul(pre[i+j-1],w);
        } 
    }
    void NTT(int *a,bool tp){
        for(int i=0;i<lim;i++) if(i<id[i]) swap(a[i],a[id[i]]);
        for(int mid=1,cnt=0;mid<lim;mid<<=1,cnt++)
            for(int j=0,len=mid<<1;j<lim;j+=len)
                for(int k=0;k<mid;k++){
                    int x=a[j+k],y=mul(pre[mid+k],a[j+k+mid]);
                    a[j+k]=Add(x,y); a[j+k+mid]=Sub(x,y);
                }
        if(tp) return;
        int invlim=inv(lim);
        for(int i=0;i<lim;i++) a[i]=mul(a[i],invlim);
        reverse(a+1,a+lim);
        return;
    }
    inline void getmul(int n,int m,int *a,int *b){
        getlim(n+m); initid();
        NTT(a,1); NTT(b,1);
        for(int i=0;i<lim;i++) a[i]=mul(a[i],b[i]);
        NTT(a,0);
        return;
    }
    inline void getinv(int n,int *a,int *b){
        static int tmp[N];
        getlim(n<<1);
        int m=lim;
        for(int i=0;i<lim;i++) b[i]=0;
        b[0]=inv(a[0]);
        for(int step=2;step<m;step<<=1){
            getlim(step<<1); 
            for(int i=0;i<lim;i++) tmp[i]=(i<step)?a[i]:0;
            initid();
            NTT(tmp,1); NTT(b,1);
            for(int i=0;i<lim;i++) b[i]=mul(Sub(2,mul(b[i],tmp[i])),b[i]);
            NTT(b,0);
            for(int i=step;i<lim;i++) b[i]=0;
        }
        return;
    }
    inline void getdao(int n,int *a,int *b){ b[n-1]=0; for(int i=1;i<n;i++) b[i-1]=mul(i,a[i]); }
    inline void getjifen(int n,int *a,int *b){ b[0]=0; for(int i=1;i<n;i++) b[i]=mul(inv(i),a[i-1]); }
    inline void getln(int n,int *a,int *b){
        static int A[N],B[N];
        for(int i=0;i<lim;i++) A[i]=B[i]=b[i]=0; 
        getlim(n<<1); getdao(n,a,A);
        getinv(n,a,B); getmul(n,n,A,B);
        getjifen(n,A,b);
    }
    void getexp(int n,int *a,int *b){
        a[0]++;
        static int tmp[N];
        getlim(n<<1);
        int m=lim;
        for(int i=0;i<m;i++) tmp[i]=0;
        b[0]=1; 
        for(int step=2;step<m;step<<=1){
            getlim(step<<1); getln(step,b,tmp);
            for(int i=0;i<step;i++) tmp[i]=Sub(a[i],tmp[i]);
            getmul(step,step,b,tmp);
            for(int i=step;i<lim;i++) b[i]=tmp[i]=0;
        }
        a[0]--;
    }
    void getsqrt(int n,int *a,int *b){
        static int tmp[N],tmp2[N];
        int m=lim;
        for(int i=0;i<m;i++) tmp[i]=tmp2[N]=0;
        b[0]=1; 
        for(int step=2;step<m;step<<=1){
            getlim(step<<1); getinv(step,b,tmp);
            for(int i=0;i<step;i++) tmp2[i]=a[i];
            getmul(step,step,tmp,tmp2);
            int inv2=inv(2); for(int i=0;i<step;i++) b[i]=mul(Add(b[i],tmp[i]),inv2);
            for(int i=step;i<lim;i++) b[i]=tmp[i]=tmp2[i]=0;
        }
        return;
    }
    void getpower(int n,int k,int *a,int *b){
        static int tmp[N];
        getln(n,a,tmp);
        for(int i=0;i<n;++i) tmp[i]=mul(tmp[i],k);
        getexp(n,tmp,b);
    }
    void getdiv(int n,int m,int *a,int *b,int *c,int *d){
        static int ar[N],br[N],tmp[N];
        for(int i=0;i<n;i++) ar[i]=a[n-1-i];
        for(int i=0;i<m;i++) br[i]=b[m-1-i],tmp[i]=b[i];
        for(int i=n-m+1;i<lim;i++) ar[i]=0,br[i]=0;
        getinv(n-m+1,br,c);
        
        getmul(n,n-m+1,c,ar);
        reverse(c,c+n-m+1);
        for(int i=n-m+1;i<lim;i++) c[i]=0;
        for(int i=0;i<n-m+1;i++) d[i]=c[i];
        getmul(n-m+1,m,d,tmp);
        for(int i=0;i<m-1;i++) d[i]=Sub(a[i],d[i]);
        return;
    }
}
posted @ 2021-01-22 21:25  ACwisher  阅读(29)  评论(0)  编辑  收藏  举报