笔记：线段树合并

线段树合并

Like that:

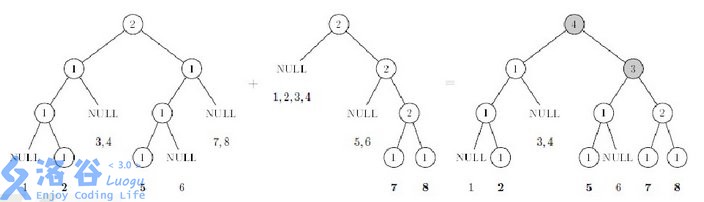
如果a有pos位置，b没有，那么新的线段树pos位置赋成a，返回
如果b有pos位置，a没有，赋成b，返回

如果此时已经合并到两棵线段树的叶子节点了，就把b在pos的值加到a上，把新线段树上的pos位置赋成a，返回

递归处理左子树 递归处理右子树
用左右子树的值更新当前节点
将新线段树上的pos位置赋成a，返回

——styx

int merge(int a,int b,int l,int r)
    {
        if(!a) return b;
        if(!b) return a;
        if(l==r)
        {
            //按照所需合并
            return a;
        }
        int mid=(l+r)>>1;
        tr[a].l=merge(tr[a].l,tr[b].l,l,mid);
        tr[a].r=merge(tr[a].r,tr[b].r,mid+1,r);
        push_up(a);
        return a;
    }

时间复杂度似乎不是稳定每次 \(O(log n)\) 但对1e5的题没问题。

---

CF600E

真 · 模板题。

每个节点一棵权值线段树，从下向上合并。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define lson tr[nw].l
#define rson tr[nw].r
const int N = 1e5 + 10;
int n,rt[N],cnt;
int e,hd[N],to[N<<1],nxt[N<<1];
LL col[N],res[N];
struct pos{
    int l, r;
    LL sum, ans;
}tr[N*50];
void add(int a, int b){
    to[++e] = b; nxt[e] = hd[a]; hd[a] = e;
}
void pushup(int nw){
    if(tr[lson].sum > tr[rson].sum){
        tr[nw].sum = tr[lson].sum;
        tr[nw].ans = tr[lson].ans;
    } else if(tr[lson].sum < tr[rson].sum){
        tr[nw].sum = tr[rson].sum;
        tr[nw].ans = tr[rson].ans;
    } else {
        tr[nw].sum = tr[lson].sum;
        tr[nw].ans = tr[lson].ans + tr[rson].ans;
    }
 //   cout<<nw<<" "<<tr[nw].l<<" "<<tr[nw].r<<"*"<<tr[nw].sum<<"*"<<tr[nw].ans<<endl;
    return;
}
void update(int &nw, int l, int r, int cl, int val){
    if(!nw) nw=++cnt;
    if(l == r){
        tr[nw].sum += val;
        tr[nw].ans = l;
        return;
    }
    int mid = l+r >>1;
    if(cl <= mid) update(lson, l, mid, cl, val);
    else update(rson, mid+1, r, cl, val);
    pushup(nw);
    return;
}
int merge(int a, int b, int l, int r){
    if(!a) return b; if(!b) return a;
    if(l == r){
        tr[a].sum += tr[b].sum;
        tr[a].ans = l;
        return a;
    }
    int mid = l+r >>1;
    tr[a].l = merge(tr[a].l, tr[b].l, l, mid);
    tr[a].r = merge(tr[a].r, tr[b].r, mid+1, r);
    pushup(a);
    return a;
}
void dfs(int u, int fa){
    for(int i = hd[u], v; i; i=nxt[i]){
        if( (v = to[i]) == fa) continue;
        dfs(v, u); merge(rt[u], rt[v], 1, n);
    }
    update(rt[u], 1, n, col[u], 1);
    res[u] = tr[rt[u]].ans; 
    return;
}
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n;i++)
        scanf("%lld",&col[i]), rt[i] = i;
    cnt=n;
    for(int i = 1, u, v; i < n; i++){
        scanf("%d%d", &u, &v);
        add(u, v), add(v, u);
    }
    dfs(1, 0);
    for(int i = 1; i <= n; i++)
        printf("%lld ", res[i]);
    return 0;
}

所以空间复杂度怎么算啊……马上又要联赛了 也不打算继续学这些东西了qwq

还没练习题目，就有点zc了。