题解 UVA11722 【Joining with Friend】

题目大意：a和b坐了两列不同的火车，且打算再车站会面。a车在\([t1,t2]\)时间段等概率到达，b在\([s1,s2]\)时间段等概率到达。火车停\(w\)分钟后出发。求碰面的概率。

解法简述：

设a在x时间到达，b在y时间到达，即\(|y-x|<=w\)时可以碰面。即\(x-w<=y<=x+w\)

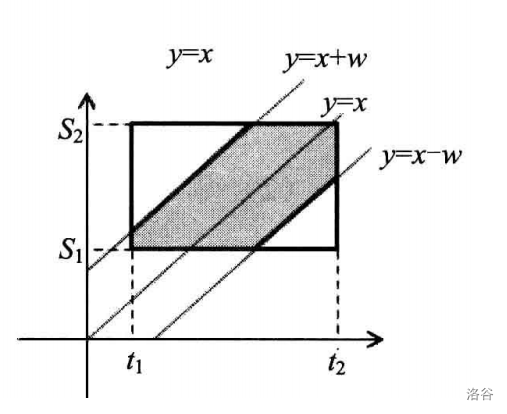
（白书配图）

所求概率就是\(S\)阴\(/S\)总

这样问题变成了如何计算阴影部分的面积。

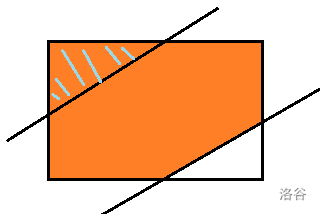
阴影面积\(=\)橙色面积\(-\)蓝色斜线面积

问题转化成计算一条直线与矩形相交后求直线上方的面积。

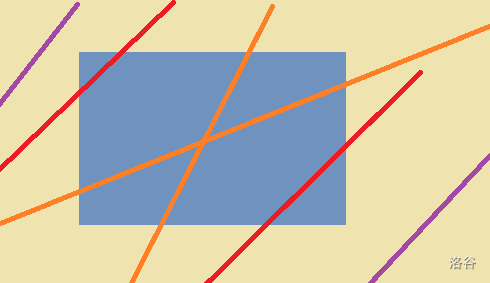
按照和矩形边的相交情况分为这六种（三组）。

左上，右下，（三角形&五边形，五边形就用矩形-三角形）

上下，左右，（梯形）

不相交&高于，不相交&低于。（0或矩形）

详见代码

代码部分

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
//const int N=;
double t1,t2,s1,s2,e;
double solve(int w){
	//y=x+w
	//上左
	if(s1<=t1+w&&t1+w<=s2&&s2<=t2+w)
		return (s2-(t1+w))*((s2-w)-t1)/2; 
	//上下
	if(t1+w<=s1&&s2<=t2+w)
		return (((s2-w)-t1)+((s1-w)-t1))*(s2-s1)/2; 
	//下右 
	if(t1+w<=s1&&s1<=t2+w&&t2+w<=s2)
		return (s2-s1)*(t2-t1)-(t2-(s1-w))*((t2+w)-s1)/2;
	//左右 
	if(s1<=t1+w&&t1+w<=s2&&s1<=t2+w&&t2+w<=s2)
		return ((s2-(t1+w))+(s2-(t2+w)))*(t2-t1)/2;
	//无交集 高于 
	if(s2<=t1+w) return 0;	
	//无交集 低于 
	if(t2+w<=s1) return (s2-s1)*(t2-t1); 
}
int main(){
	int t;
	scanf("%d",&t);
	for(int cas=1;cas<=t;cas++){
		scanf("%lf%lf%lf%lf%lf",&t1,&t2,&s1,&s2,&e);
		printf("Case #%d: %.8lf\n",cas,(solve(-e)-solve(e))/((s2-s1)*(t2-t1)));
	} 
	return 0;
}