马尔科夫决策过程和Bellman方程

要求：

1.能够检测到理想的状态

2.可以多次尝试

3.系统的下个状态只与当前状态信息有关，而与更早之前的状态无关，在决策过程中还和当前采取的动作有关。

马尔科夫决策过程由五个元素组成：

S:表示状态集（states）

A:表示一组动作（actions）

P:表示状态转移概率P_sa表示在当前s∈S，经过a∈A作用后，会转移到的其他状态的概率分布情况。在状态s下执行动作a，转移到s'的概率可以表示为p(s'|s,a)

R:奖励函数，表示agent采取某个动作后的即时奖励

y:折扣系数，意味着当下的reward比未来反馈的reward更重要 Σγ^tR(s_t) 0≤γ<1

 

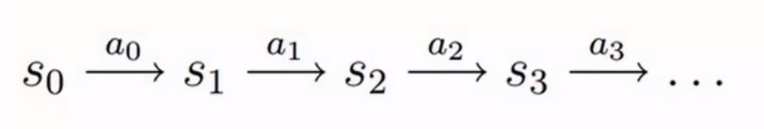
上图即为决策过程，可以大致描述为，智能体初始状态为S0，选择一个动作a0，按概率转移矩阵Psa转移到了下一个状态S1，由此反复。

在马尔科夫决策模型中，有一个状态价值函数：v(s) = E(Ut|St = s)，表示t时刻状态s能获得的未来回报的期望，用来衡量某个状态或者状态-动作对的优劣价值，累计奖励的期望。从而就有最优价值函数 v_*(s) = max v(s) （表示所有策略下最优累计奖励期望）

Bellman方程：当前状态的价值和下一步的价值及当前的奖励（Reward）有关　　

Bellman方程用如下公式表示(其中π是给定状态s下，动作a的概率分布，γ为折扣系数)：

v_π(s) = Σ_a∈A π(a|s)（R_s^a + γΣ_s'∈S P_ss'^a v_π(s')）

P_ss'^a = P(S_t+1=s'|S_t=s,A_t=a)

v_π(s) = E_π [R_s^a + γ v_π(S_t+1)|S_t =s]

可以理解成，在某状态s下，当前奖励为R_s^a，对于a‘∈A和s，会有相应的后续一个或多个状态s'，这时需要求每个后续s'对应的价值和其发生概率的乘积，从而计算出bellman中的v_π