20373222李世昱第一单元总结

第一单元总结

第一部分 代码架构迭代逻辑

第一次作业类图如下:

 

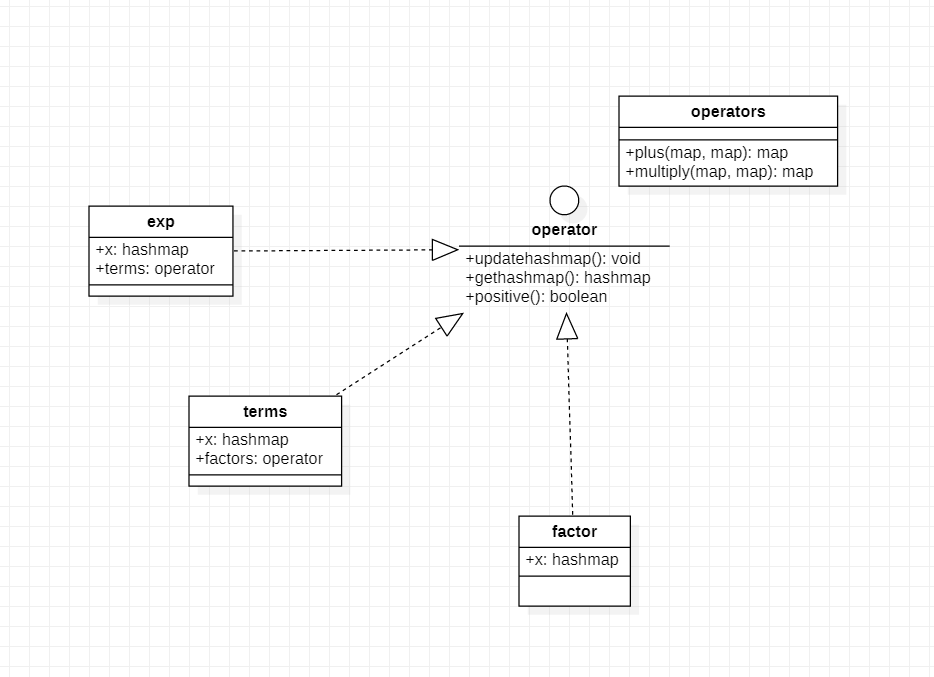
核心思路：仿照trainning中递归下降的做法，开三个对应结构的类:exp(表达式),term(项),factor(应该说最简因子)，对文本起分析的类如Lexer,parser等由于和trainning差距不多，思路也都较为固定，这里不做展示。

1：如何解决化简问题？

　　我们发现最终结果总可以表示为x的多项式，a0X**0+a1x**1+...这样我们可以开一个hashmap，把x的指数作为键值，这样每个表达式唯一对应一个hashmap（举例来说：-x**2 +2*x就唯一对应{2:-1,1:2}），同时每次运算的时候就可以指数相同自动化到最简。

->这样我门确定了最终答案的合并方法：hashmap自然合并

 

2:  如何处理看起来很麻烦的因子？

　　三种因子，x幂函数，常数，表达式因子。我们可以把常数因子视为一种x的0次幂的幂函数，这样和x幂函数一同作为基础因子，而表达式因子则直接去new一个表达式类型的对象，那么很显然term里面就会混有多种类型的对象，如果我们一个个把他们区分开再调用各自的方法显然是一种很不美观的做法，为次我想让这几个类型达成某种功能上的统一，这就有了类图站在C位最显眼的接口：Operator接口（这个接口后文称为"算子协议"或者"算子接口"）。那这个接口里面要放什么函数呢，对应函数又要如何实现，着我们就得仔细分析一下完整的流程。

->我们采用Operate接口来统一处理

 

3：算子接口中要什么功能？

　　我们先分析一下完整流程，我们拿到一个可爱的小表达式，先用词法分析器一顿分析，得到了一个类树的结构，上层的对象的容器中放着子对象。不论是什么对象，我们要得到最终的hashmap，我们需要他把他的数据结构，也就是list容器所蕴含的结构信息，转换成hashmap，也就是我们要的答案。然后对于高级的对象，他需要让所有子对象把他的hashmap准备好，term对象只要把这些相乘就好，exp对象则是相加，而对factor对象来说则不用处理。与此同时我们发现化简的过程不必在意子对象究竟是什么，仅仅要求子对象把他的hashmap乖乖准备好并且暴露出来，我就可以进行自己的化简了。这样我们确定了算子协议所需的两个函数：用于让子类更新准备hashmap的update()，用于暴露出自己的hashmap的getHashmap()函数

->update();getHashmap();

 

4:迭代开发考虑？

　　可以从类图上看到，用于具体化简exp,term的具体运算方法并没有写入对应的对象中，而是提取出来另开一个Operators（之后称为运算大类）类，主要是出于以下考虑：如果要加入新的结构类型（地位类似于exp,term等），这个类型的化简可能要重复利用hashmap的加法乘法化简，把计算方法独立出结构中以便后续的重复利用。

 

 

至此，第一次作业已经可以轻松解决，第一单元我认为的难点在于第一次到第二次的迭代思路，我将在下文详细一步一步推出新架构的架构方法

顺带一提，我的第二次作业不小心直接完成了第三次作业，所以只有一次迭代（

 

 

先不放类图，我们尝试从第一次架构迭代成第二次的架构：

先分析一下问题：

1.新加入了三角函数

2.新加入了自定义函数（这里sum函数和自定义函数处理有类似之处，放在一个问题中）

3.变量XYZI，第一次的hashmap不能记录记录全部信息，需要换一个结构。

我们先从第三个问题入手：

 1.多变量如何化简？

　　我们先不考虑sin，这里两个多项式x**2y**1z**3   z**3x**2y**1,，我们知道他俩能化简的依据是变量一样，对应相同变量的幂次也一样，那么我们稍加思考，我们如果把一种表达式类型进行规则化的表达，就可以简单的进行化简了。所谓规则化的表达，简单来说就是输入或者hashmap遍历的无序不影响结果（这一点后面还会用到）。在这里我们如果人为构造一个字符串，先按照字典序把所有变量排序，再按照变量名字+变量次数的格式输出，举例来说上面两个多项式，他们都会被化简为x2y1z3，那么我们可以通过这个量来作为化简依据。

　　因此我们仍采用hashmap来进行自动化简，在上一次我直接用指数，也就是一个bigint变量作为键，而在这次为了表达更多的信息，我们新建一个类，这个类的唯一用处就是暴露出化简的依据。这里我给他起了个文艺点的名字-- “抗原”，如果你在后文看到“暴露出抗原”等字样不要怀疑走错了 。

　　具体实现中，抗原类内部仍有一个hashmap，类型为<string,Bigint>,表示名字为String的变量和他的次数。抗原需要显示的暴露出合并的依据，这里命名为hashStr，也就是上文提到的x2y1z2。此外他需要时刻更新他的hashStr,所以每次尝试修改抗原类的hashmap时，都会调用一次自更新函数。抗原类作为键要提供equal和hashcode函数，这里很显然我们的合并依据就是hashStr ,所以直接调用hashStr的equal和hashcode就可以啦。

->我们新建一个“抗原类”，作为多变量化简的依据

 

2.三角函数如何解决？

　　三角函数我们还是要给他新建一个类的，他有个唯一一个子类结构，也就是三角函数内部。为了之后的可迭代性着想，我们直接把难度升满，三角函数内部什么都可以，换言之里面是个表达式的结构。如何让三角函数融入体系？伟大的算子协议教导我们：我化简不关心你是谁，乖乖更新并暴露出hashmap就好。在此前的架构中我们的结构容器，也就是各个类存储子对象的list中，用的都是算子类型，这样我们要是想加入新的类，仅仅需要让他遵守算子协议，其他的根本需要改。

　　三角函数如何化简呢？我们这里先做最简单的化简，也就是仅仅对sin指数相同并且内部完全一样的三角函数进行合并，如sin(x+1)**2  + sin(x+1)**2。看到这里，你是否想起了什么？要是没想起来建议重新读一遍第一问 没错，如果我们把sin内部的规则化的表达 ，把sin连同内部作为一个崭新的变量的名字（上式就把sin(x+1)看为新的变量，地位等同于x），指数作为这个变量的指数，sin非常自然的融进去了，我们根本不需要对其他类做任何处理！

　　不过凡事是由代价的，我们把三角函数视为一个变量，那么他就失去了他作为三角函数的独特性，因此采用这种方法会在进一步的三角化简中带来麻烦。由于时间原因本人最终代码中是没有三角化简的，不过有设计如何进行三角化简，会在后文进行说明。

->视为崭新的变量，不需要做额外处理

 

3.自定义函数？

　　先谈谈为什么会涉及到克隆的问题。我们的自定义函数本质上是一个表达式对象，如果我们要多次调用，就要多次赋值，而用的都是一个表达式，显然会造成错误的结果。所以我们每次调用函数要复制出一个一摸一样的表达式。深克隆具体实现很简单这里不多说。自定义函数赋值的过程本质上就是最简因子的替换，检查抗原正确符合的因子并且把他删除，把实参的克隆加入到项里面就可以了，实现起来还是非常简单的。

 

4.三角函数的进一步化简？

　　这部分由于时间原因我代码中没有实现，所以也不会过多介绍。一个很简单的思路就是用正则表达式提取出所需要的抗原，然后进行简单的字符串的简单替换形成新的hashStr，再反向生成抗原加入到hashmap中就可以了。举例来说比如我们要化简cos**2 + sin**2，我们用正则捕捉到最外层的cos()**2,然后把cos这部分去掉反向生成一个抗原，另外把cos字符串替换为sin得到有一个抗原，把系数分别置为cos这项的系数的复制和相反数，就实现了cos**2 = 1-sin**2的变换。

以下就是第二次第三次作业的类图：

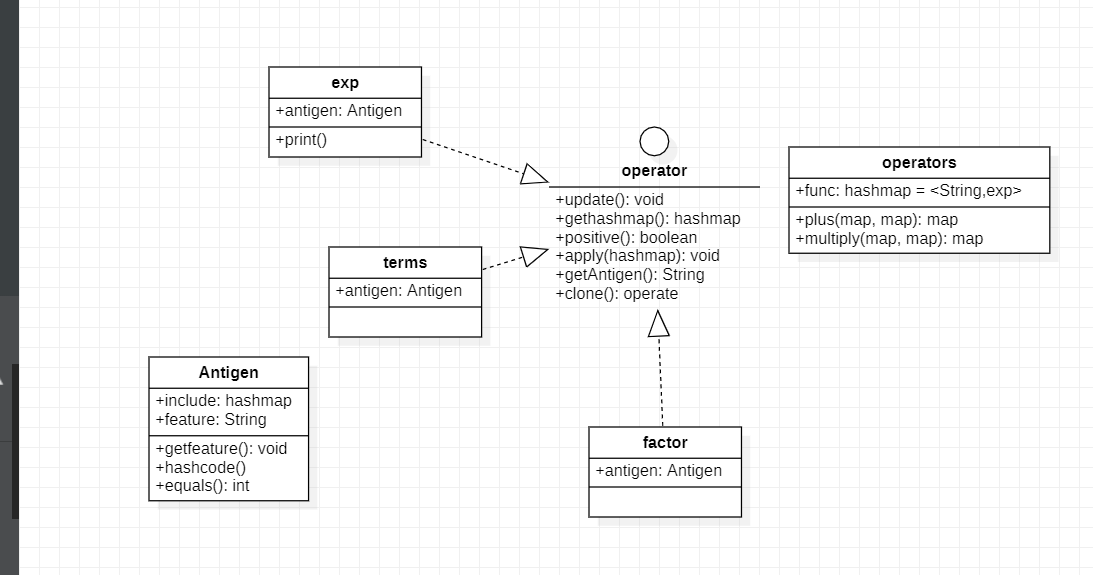
（类图是在写代码之前做的，所以一些变量名字对不上，如feature是上文所述的hashStr）

 至此代码架构逻辑已全部讲述完毕。

总体而言，这个架构优点在于架构简单思路清晰实现容易，如果不做优化只是做最简单的合并只需要很少的代码量，代码中容器都是统一的Operator类型，减少了思考量；缺点在于过于归一化的设计降低了不同银子不同类的区分度，在三角函数化简中增加了难度。

 

第二部分 代码度量

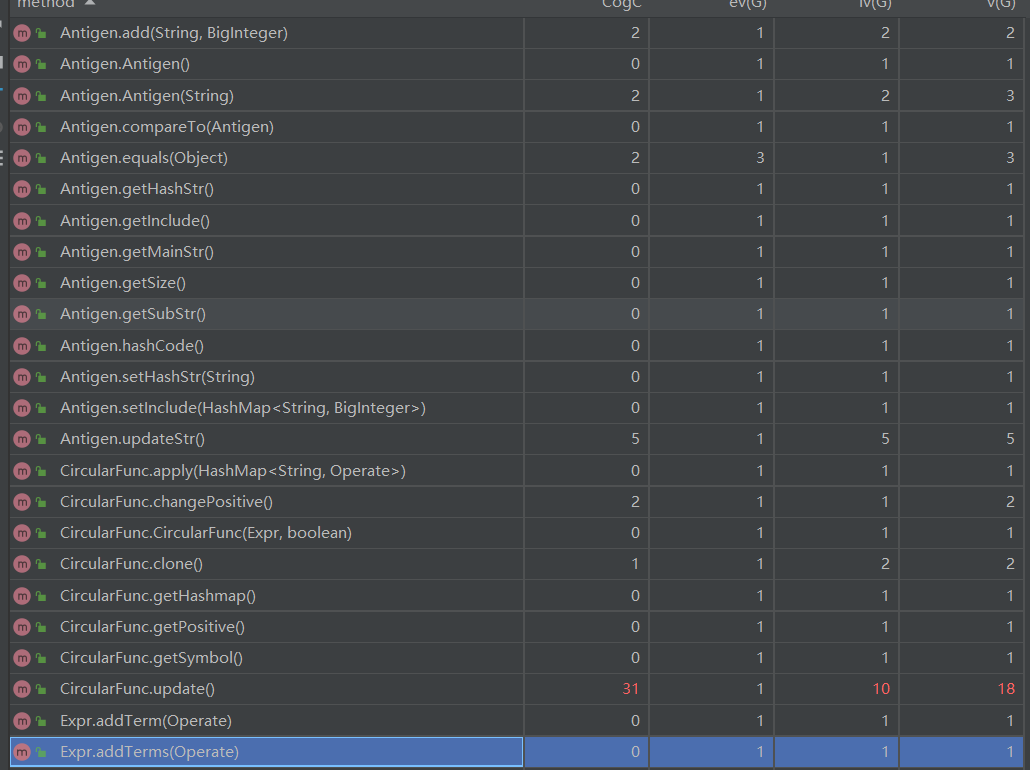
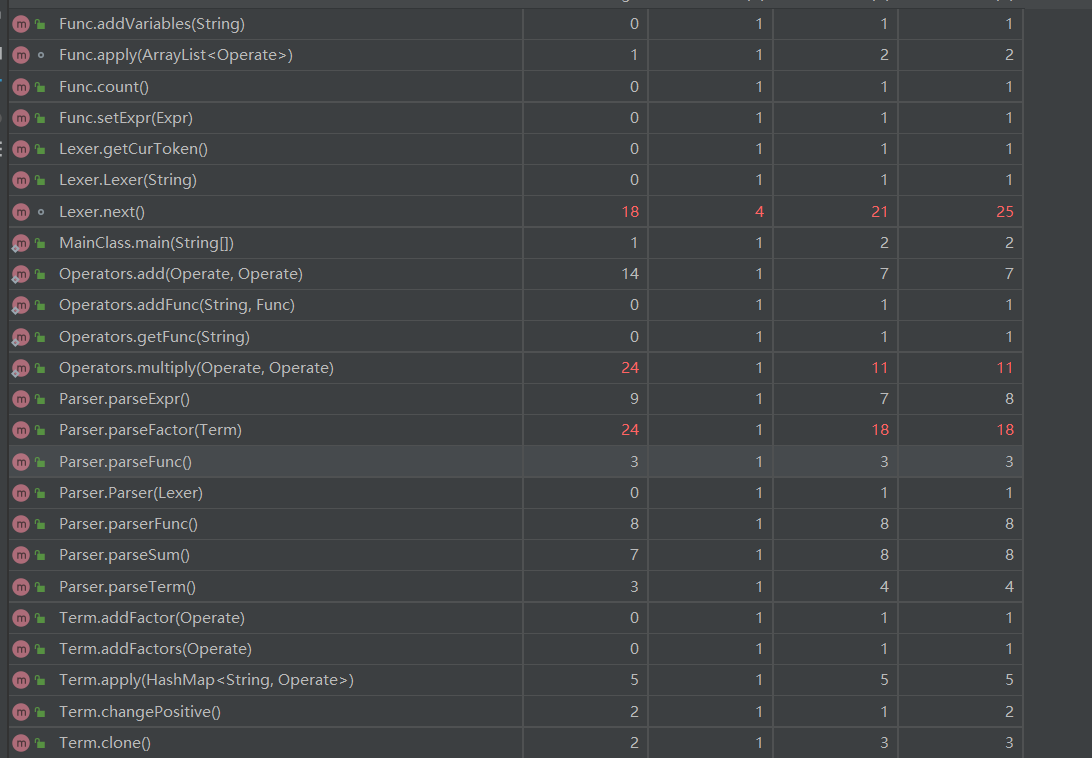
函数总共约有70多个，有十多个函数具体没有用上（一键生成了）明显标红的几个函数，可以看出来很多都与优化有关：

　　三角函数的update函数中内部做了正负号化简处理.表达式的print函数，optimize（未实现注掉了），getpositive都是用于规格化并且简化输出，考虑的情况比较多，具体实现上也会更加复杂。但是词法语法分析中我把sum 自定义函数等几乎全写入读取因子函数中，导致读取因子和耦合度过于高了，应该把不同类型的读取抽离出来减少耦合度，这一点我处理的不好。

　　接下来看类的耦合度

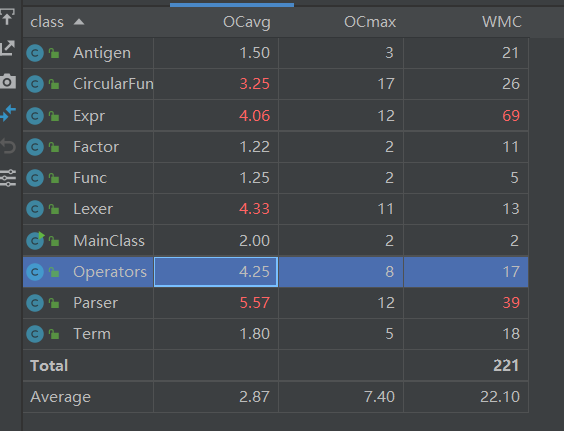
　　这里我有一些混用的地方，在上一次的架构中Operators的存在只是为了方法的复用，我图方便把自定义函数容器也放入Operatoes中，导致耦合度过高了。三角函数和表达式其实处理起来很简单的，都是把责任推给下家，但是由于写了比较复杂的优化函数极大的增加了复杂度。对于不应该有如此高耦合度的地方我会吸取教训在下次设计中改进。

 

第三部分 BUG

　　说来惭愧，这个代码在第三次强测中挂了一个点，并且被hack两次。这个bug表现为sum中的终点数字如果为负数就会爆0，bug产生原因并不是结构上的问题，而是单纯的复制粘贴代码的时候（复制处理第一个数字的代码），忘记修改了一个量，这个bug在第二次没被测出来，倒在了第三次强测下。我有做过自动测试和自动数据生成，但是不幸的是sum内部只考虑了生成正数的情况，导致未能测出bug，深感遗憾，这里分享一下数据生成的逻辑。

　　数据生成也是按照递归下降的思路，表达式生成器随机一个数字要求生成这么多个项，项同理生成随机多个因子乘号连接，因子再随机生成表达式，自定义函数，三角函数，sum函数等，具体实现还是比较简单的，这里说一下测试的心得。我生成的第一次数据，2k条数据和别人对拍，对拍没问题但是他被hack了，bug原因是表达式后面的空格会造成异常，并且我看我生成的数据大多都是很长的表达式，无法检验极端情况。为此我做出了一些改进，全局一个布尔值极限测试，当极限测试为true的时候，大幅度减少项和因子随机数量的上限，产生的随机数字以极高的概率出现 0 1 -1，并且有小概率出现intmax，这样修改之后自动生成数据已经可以做到覆盖很多极限情况,长度原因仅仅展示一小部分，实际中数据比展示的还要极限，我在检查数据强度也看到了类似于sin(0)**0 +-(+-0)**0这种很极限的数据，整体而言数据强度还是很不错的，虽然没有测出我的sum函数bug，不过在我刚做完的时候以及互测环节还是测出来不少bug。

 

　　对拍程序则是参考了讨论区的做法，用了python的库，带入十个点检验是否相等，不是原创这里不多介绍。

　　有了这些，测试别人的bug我是直接选择极限数据黑盒测试跟我自己代码对拍，由于数据强度还算可以，测试效果还是很显著的，第三次互测中抓了别人五个bug（第一刀直接三杀）。

 

第四部分 心得体会

　　整体第一单元做下来还是感觉比较简单的，第二次作业给之后迭代留的自定义名称变量（变量名字不限于xyzi），任意嵌套（嵌套可以任意嵌套），以及预想了求导 e*x lnx 怎么处理现在都没有用上。我觉得能轻松完成第一次作业要归结于以下两点：第一点在于提前留好迭代窗口：也就是提前猜测一下后面会如何迭代，甚至可以顺手直接实现。我身边不少人第二次作业到第三次作业迭代中几乎没怎么动代码，第三次新增的内容完全在第二次预留的迭代处理中，极大的减少了OO课程锁占用的时间。第二点我想在于提前架构好UML类图再去实现代码，在架构好UML之后理顺一遍完整的实现逻辑，打代码的时候几乎不会停顿，时刻知道自己要去实现什么，这个函数是为了什么。第一次作业我是周三晚上八点架构完UML类图，当天就完成了所有代码（bug是第二天怼的）。在架构设计中就要提前想好重要的函数的大致的实现过程，并且忽略不重要的细节如lexer实现等，并且给自己后续可能追加的优化留出地方，留出空间，如我在架构中设计了三角函数的优化，可以从抗原类的代码中中看出来预留给后续优化的部分（如传入字符串的构造函数，正常情况下是不需要字符串构造的，仅仅在三角化简中便于处理所以写的这个生成函数）。总而言之，在写代码之前设计好完整的架构是很重要的，不仅减少bug数量，还可以提高代码速度。

　　以上文章若有不正确或者处理不好的地方，还请老师助教同学们不吝赐教！