CSP 日照集训考试 Day2
考的并不好。主要整理整理错因,并不是为了写题解。
T1


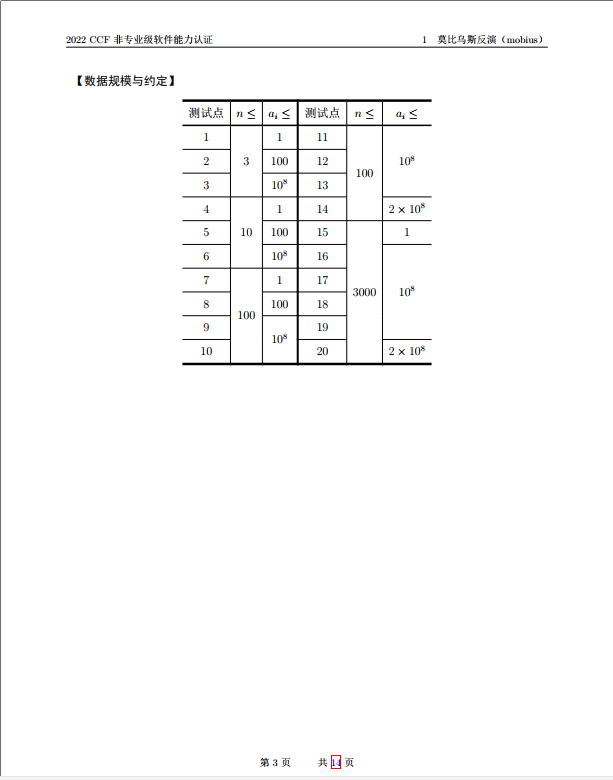
很简单的题,让我搞成了 70 pts
考场上想的是预处理出第 i 位之后 j 出现的次数,然后枚举两个位置,求一下 gcd ,找一下后面出现的次数。
然后粗略的算了一下复杂度,嗯。大概是 \(O(n^2 log~n)\) 左右的,然后看了眼数据范围。行了,应该能过,然后就没再管它。
五分钟码完了。
可以发现,常数不小,已经超过 1e8 了。
所以我挂了,丢了 30 pts
考虑一下,可以优化掉预处理,在计算的时候第二个位置倒着枚举就好了。
赛时代码
map <pair <int, int>, int> vis;
int a[3007];
int main () {
int n; cin >> n;
for (int i = 1; i <= n; ++ i) cin >> a[i];
for (int i = 1; i <= n; ++ i) {
for (int j = i + 1; j <= n; ++ j) {
vis[make_pair (i, a[j])] ++;
}
}
int ans = 0;
for (int i = 1; i <= n; ++ i) {
for (int j = i + 1; j <= n; ++ j) {
int Gcd = gcd (a[i], a[j]);
if (vis[make_pair (j, Gcd)]) ans += vis[make_pair (j, Gcd)];
}
}
cout << ans;
}
T2



可以想到 dp ,以 i 位结尾,最长的满足条件的子序列。
因为要算一个最小的 k ,使得子序列相邻两位之间的差值要小于等于这个 k ,并且能使这个子序列能够达到 m 的长度。
我们不好直接算 k 。
所以考虑二分答案,因为如果较小的长度能够满足的话,更长的长度就一定能满足,所以满足单调性,可以二分。
二分后,\(O(n^2)\) 的 dp ,算一下最长的子序列能不能达到 m 的长度即可。
# include <bits/stdc++.h>
using namespace std;
#define ll long long
const int D = 1007;
int n, m;
ll a[D];
int f[D];
bool check (ll mid) {
int res = 0;
if (n >= 1) res = 1;
for (int i = 1; i <= n; ++ i) f[i] = 1;
for (int i = 1; i <= n; ++ i) {
for (int j = i + 1; j <= n; ++ j) {
if (abs (a[i] - a[j]) > mid) continue;
f[j] = max (f[j], f[i] + 1);
res = max (res, f[j]);
}
}
if (res >= m) return 1;
return 0;
}
int main () {
cin >> n >> m;
for (int i = 1; i <= n; ++ i) cin >> a[i];
ll l = 0, r = LONG_LONG_MAX, ans;
while (l <= r) {
ll mid = l + r >> 1;
if (check (mid)) r = mid - 1, ans = mid;
else l = mid + 1;
}
cout << ans;
return 0;
}
T3
考试的时候以为能做出来呢。两个半小时浪费在这十分上了。
顺一下自己想到什么程度了吧。
读完了题,就有一个简单的思路:
就是如果某个节点只有一个子节点的话,那将他填满只需要让这一个儿子填满;如果有多个儿子的话,就要将所有儿子填满,看起来挺废话
如果前面一个儿子填满了,因为这个填满了的儿子的子节点与父亲怎么填没有关系了,那就可以将前一个儿子的所有儿子的石头都拿过来,给这个儿子用。
以此类推,将所有儿子填满。
刚开始觉得这样就能做出来。
十分钟把这个 dp 打出来了,大样例过不去。
于是我手造数据,造了一个不能说没用,但是倒不如说成了我这次考试累赘的一个例子,因为造的不太特殊,导致我只发现,算子节点的时候,放石头的顺序不同,那花费石头的个数就不同。
然后我,使劲对着这个例子拖拉,扒拉了半天,手膜了半天,看出来是需要排序才能做出来的一道题。
具体的蒙不出来。
然后只剩了十分钟了。
交了一个假的 dp 。
# include <bits/stdc++.h>
using namespace std;
const int D = 1e6 + 7;
int n, cnt;
int head[D], f[D], ason[D];
struct edge {
int nxt, to;
}line[D << 1];
int a[D];
void add (int u, int v) {
line[++ cnt].nxt = head[u];
line[cnt].to = v;
head[u] = cnt;
}
vector <int> tmp[D], g[D], p[D];
void dfs (int x, int fa) {
bool bz = 0;
int lst = 0;
for (int i = head[x]; i; i = line[i].nxt) {
int y = line[i].to;
if (y == fa) continue;
bz = 1;
dfs (y, x);
g[x].push_back (f[y]);
tmp[x].push_back (ason[y]);
p[x].push_back (y);
}
if (!bz) {
f[x] = a[x];
return;
}
// if (x == 2) cout << f[x]<<" " <<lst << "|\n";
for (int i = 0; i < g[x].size (); ++ i) {
if (g[x][i] > lst) {
f[x] += g[x][i] - lst;
lst = tmp[x][i];
}
else lst -= a[p[x][i]];
// if (x == 1) cout << f[x] << " " << lst << "\n";
}
if (lst < a[x]) f[x] += a[x] - lst;
}
void getson (int x, int fa) {
for (int i = head[x]; i; i = line[i].nxt) {
int y = line[i].to;
if (y == fa) continue;
getson (y, x);
ason[x] += a[y];
}
}
int main () {
freopen ("ttt.in","r",stdin);
freopen ("ttt.out","w",stdout);
cin >> n;
for (int i = 1; i < n; ++ i) {
int x; cin >> x;
add (i + 1, x);
add (x, i + 1);
}
for (int i = 1; i <= n; ++ i) cin >> a[i];
getson (1, 0);
dfs (1, 0);
for (int i = 1; i <= n; ++ i) {
cout << f[i] << " ";
}
}
/*
9
1 1 1 1 2 3 4 5
4 3 2 1 5 7 10 13 6
19 10 12 14 11 7 10 13 6
*/
依稀可见调试的痕迹。
T4
看了一眼,感觉很像三色二叉树那个题,码上了,过了样例,然后发现了不对劲,题目里有数量限制…
一般来说我应该知道要怎么设状态的阿……不知道为啥没想出来,大概是受 T3 的影响。
然后我就打着侥幸的心理,在某些 sub 上用了这个算法去求解,虽然没得分吧。然后游离到了 T3 。
到最后看见了剩的时间不多了,开始打这个题的暴力。
当时差不多是五点五十了,眼看着 T3 就像是想不出来的样子了,开始打 T4 暴力。老师当时都说要交卷了……我五分钟打完了,编译一下,然后过样例了……离谱
题解明天上午整理。
总结一下,感觉收获不少的。
首先不能再大意了,我有时候经常就是,没读完题,就开始做,过于心急,导致很多代码都是白打的,时间都在这些上面浪费了。再就是这次是真知道了不能死磕一道题,会死的很惨,不会就是不会,我甘拜下风,别人的头脑就是灵活,我没必要跟人家拼那个脑子。既然思维不够,那基础的一定要拿到,比如第三题我赛后看见,出题人真的给了好多的部分分,这感觉就像去年似的,只喜欢打正解,特看不起部分分,导致去年的我多次倒数。至今我倒是又回去了?幸好不是 CSP ,以后能注意的。
以下是明天的工作了。
题解:
T1,2 参上
T3
今天回来看了一会就看出来了。原来也不是那么难。
就是对每个点记录一个 f[i] ,表示要想让这个点能被填满,最少需要多少个石子,las[i] 表示填完了这个点,可以把子节点的石头都拿过来,能拿多少个。
然后只考虑两个儿子的情况:
一个叫 x ,一个叫 y 。如果先放 x ,那花费石头个数就是 f[x] + f[y] - las[x] ;如果先放 y ,那花费石头个数就是 f[y] + f[x] - las[y] 。
关系就是 f[x] + f[y] - las[x] ? f[y] + f[x] - las[y] 。"?" 表示一个符号。
化简就是 -las[x] ? -las[y] ,要尽可能的让花费少,那就尽可能让 -las[i] 小,那尽可能的让 las[i] 大的先填。
所以算每个点的时候要先按照 las[i] 对子节点排序。
然后再算贡献。
# include <bits/stdc++.h>
using namespace std;
const int D = 1e6 + 7;
int n, cnt;
int head[D], f[D], ason[D];
struct edge {
int nxt, to;
}line[D << 1];
int a[D];
void add (int u, int v) {
line[++ cnt].nxt = head[u];
line[cnt].to = v;
head[u] = cnt;
}
bool cmp (int x, int y) {
return f[x] - a[x] > f[y] - a[y];
}
void dfs (int x) {
vector <int> b;
for (int i = head[x]; i; i = line[i].nxt) {
int y = line[i].to;
dfs (y);
b.push_back (y);
}
sort (b.begin (), b.end (), cmp);
int las = 0;
for (int i = 0; i < b.size (); ++ i) {
int y = b[i];
f[x] += max (f[y] - las, 0);
las = max (las - f[y], 0);
las += f[y] - a[y];
}
f[x] += max (a[x] - las, 0);
}
int main () {
// freopen ("1.in","r",stdin);
// freopen ("ttt.out","w",stdout);
cin >> n;
for (int i = 1; i < n; ++ i) {
int x; cin >> x;
add (x, i + 1);
}
for (int i = 1; i <= n; ++ i) cin >> a[i];
dfs (1);
for (int i = 1; i <= n; ++ i) {
cout << f[i] << " ";
}
}
/*
9
1 1 1 1 2 3 4 5
4 3 2 1 5 7 10 13 6
19 10 12 14 11 7 10 13 6
*/


