莫队_Part three

树上莫队

原来莫队还能上树

算法简介

很多数据结构都是用某种方法，把树变为序列进行操作。

例如树链剖分，使用用 \(dfs\) 序把树强行变成一个序列。

为了发扬这种好用的做法，树上莫队也采用了相似的做法，但它使用的是括号序 \(qwq\)

括号序

定义

括号序，是一种 \(dfs\) 序，实际上是模拟了栈。先序遍历整棵树，对于树上每一个点，我们会在括号序中记录他的入栈出栈时间。

如下图：

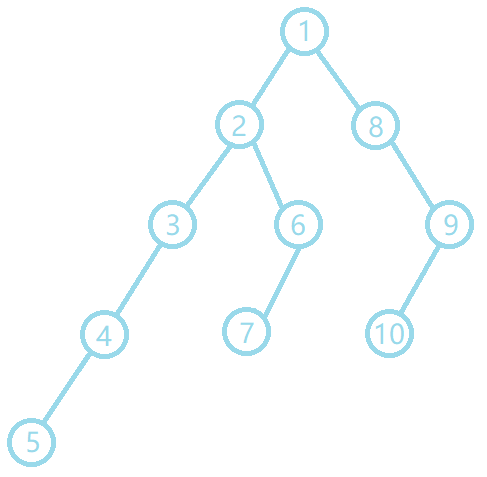
该图的括号序为：\([1,2,3,4,5,5,4,3,6,7,7,6,2,8,9,10,10,9,8,1]\)

遍历过程中顺便记录两个下标，用 \(fir[x], las[x]\) 分别表示每个节点的入栈出栈时间。

例题

给定一棵 \(n\) 个节点的树，每个节点都有一个颜色，每次询问一条路径上的不同颜色有多少种。

首先，我们已经知道怎么在序列上计算颜色种类。

考虑用括号序处理这个问题。

<1> 如果一个点在另一个点的子树中。

例如要查询从 \(2\) 到 \(7\) 的路径，在该图的括号序中截取 \([fir[2], fir[7]]\) 这一段。

这一段区间为 \([2,3,4,5,5,4,3,6,7]\)，其中 \(3,4,5\) 出现两次，说明这三个点进入一次栈后又出去了，那在统计答案的时候标记是否已经经过这个点了，如果第一次经过，那就add(x)，否则del(x)。与括号序能狗完美配合qwq。

<2> 选择的两点没有祖孙关系

例如查询5到7的路径，考虑在括号序中取[las[5], fir[7]]这一段。

正确性：对于5到lca(5,7)即2的路径上的点是只出不进的，只统计了一次，然后从2到7的路径上的点按照第一种情况考虑。

发现这段区间没有lca(5,7)，所以最后add(lca(5,7))。