生成树_Part three

kruskal重构树

Problem

已知图G，每次询问给定一个位置，长度和k，问 从这个点出发，只能经过不大于这个长度的边，到达的点中，点权第k大的点权是多少。

提示

看到题目中有这句话“只能经过不大于这个长度的边”，就知道，一定与最小生成树有关，因为最小生成树中的边一定是边权最小的，如果不按这些边走，就会死掉了qwq。

定义

在跑kruskal算法过程中，按边权从大到小加入若干条边，我们依照这个顺序构建的树，叫做kruskal重构树。

构建方法

首先将每个点看做一个集合，也就是初始时有n个集合，每个集合有一个点，点权为0

kruskal过程中，加边操作会合并两个集合，我们可以新建一个点，点权为加入边的边权

同时将合并的两个集合的跟作为新建点的左儿子和右儿子。

然后我们将集合和新建节点合并为一个集合。将新节点设为根。

n-1轮后，我们得到了一颗恰好有n个叶子的二叉树。这棵树就叫做kruskal重构树。

举个例子qwq：

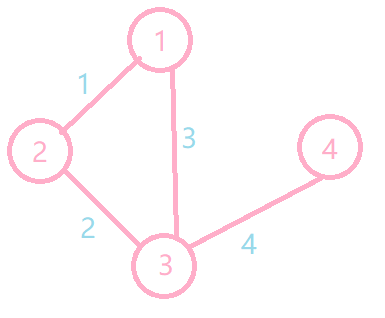
他的重构树长这样：

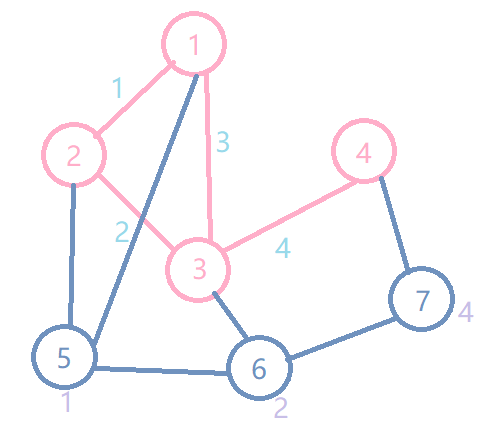
把它弄的像树一点：

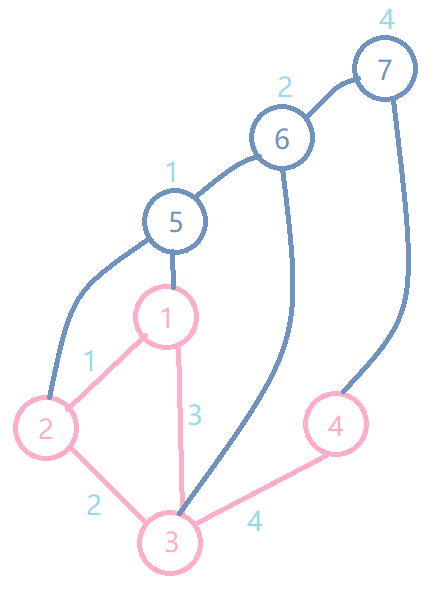
由此可以发现kruskal重构树有一下性质：

• 每个节点的权值一定大于它子树中任意一个点的权值，因为构造最小生成树的时候权值越大，出现越晚，距离根越近。
• 所以每个点对应的子树都是一个每个点权值小于等于该点权值的连通块

解决方案

由于kruskal重构树的性质，可以得到如下解决方案：

设每次查询中，当前点为x，长度为l，询问第k大点权。

对全图跑重构树算法，因为重构树上的点权从根到叶子是单调递减的，所以可以从根节点向下跑倍增，找到第一个小于等于l的点权的点。

只要x是这个点的子树中的点，那这个点的子树就是x能够到达的点。

因为重构树上每个点都有自己的编号，也就是dfs序，在构建重构树之后，对整棵树建主席树，求子树中k大值即可。