生成树_Part two

瓶颈生成树

定义

无向图G的所有生成树中，最大边权最小的生成树为瓶颈生成树。

最小生成树与瓶颈生成树的区别。

最小生成树一定是瓶颈生成树，但是瓶颈生成树不一定是最小生成树。

证明

关于最小生成树一定是瓶颈生成树这一命题，可以运用反证法证明：我们设最小生成树中的最大边权为 w，如果最小生成树不是瓶颈生成树的话，
则瓶颈生成树的所有边权都小于 w，我们只需删去原最小生成树中的最长边，用瓶颈生成树中的一条边来连接删去边后形成的两棵树，得到的新
生成树一定比原最小生成树的权值和还要小，这样就产生了矛盾。

证明其实不用看，因为根本看不懂，最简单的证明就是举例

如图：

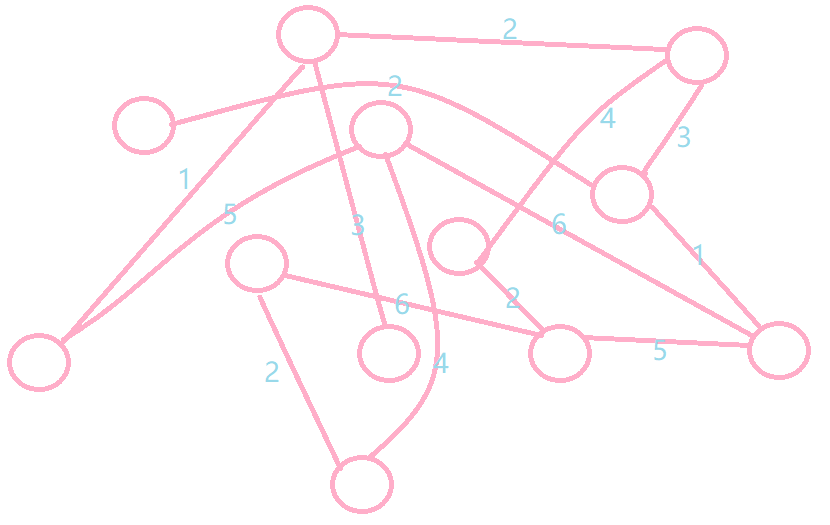
证明过程：

• 求出最小生成树：
  

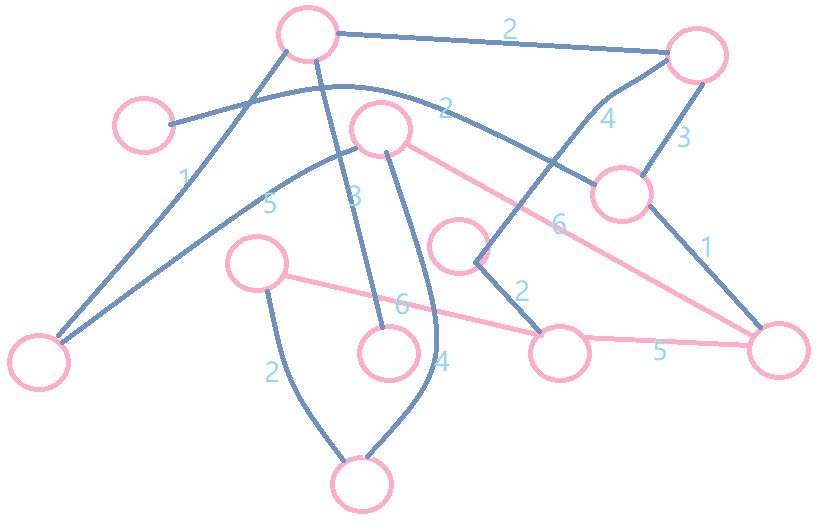
• 加入一条边，边权小于等于原图中最大边权，加入后形成环，删除环中除加入边外的一条边：

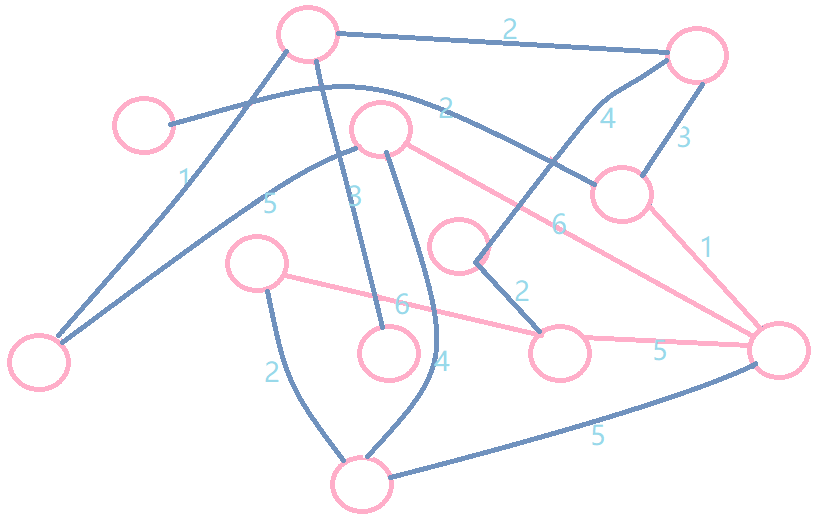
形成的树与最小生成树不同，且改树为最小瓶颈树。

以上例子纯属自造，但，是正确的qwq