可持久化

在 \(oi\) 中，很多时候我们需要知道我们的数据对于以前变化了多少。

但是很多算法和数据结构本身没有这种功能。

所以我们需要这样一个高级数据结构。

主席树

主席树，也可称为可持久化线段树，因为它本质上就是维护了一个可进行操作的数组，所以主席树，也可称之为可持久化数组。

主席树的主要思想是，对于每次操作，重新构造一颗树，将它的根记录下来，以便以后使用。

但是有这样一个问题，对于较大的数据范围，比如 \(N = 1e6\)，每次操作我们都要重新建一颗新树，那空间不久爆炸了 \(qnq\)，这不好，所以我们想到了一个方法，不需要修改的节点信息不动它，直接连上操作之前那棵树上对应节点就行；对于需要修改的点，我们才重新建一个点。那这样空间复杂度就大大降低了\(qwq\)

口胡的不太形象，画个图图：

首先我们构建一颗树

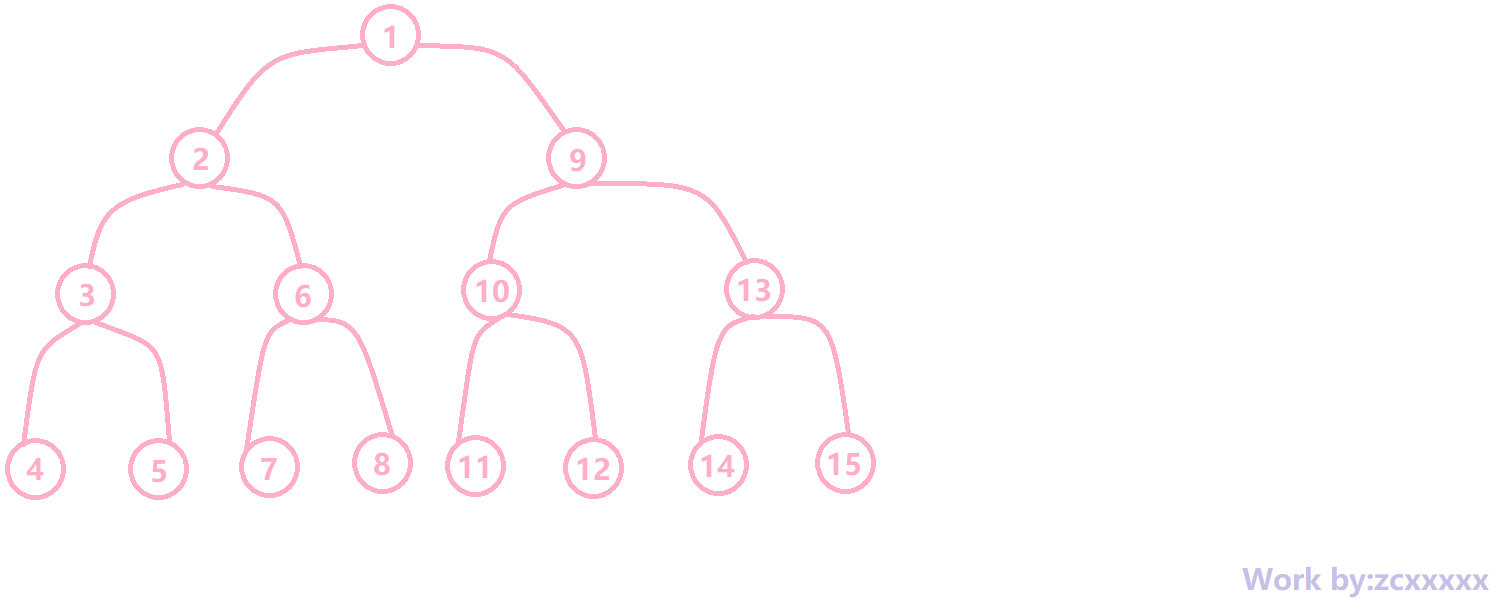
如 \(page1\) ，每个节点的编号一定是这样的，因为构建主席树的时候是使用的一个变量确定的节点编号，在后面的代码中可以看粗来，而且建树过程构成了中序遍历，所以树严格长这个样qwq

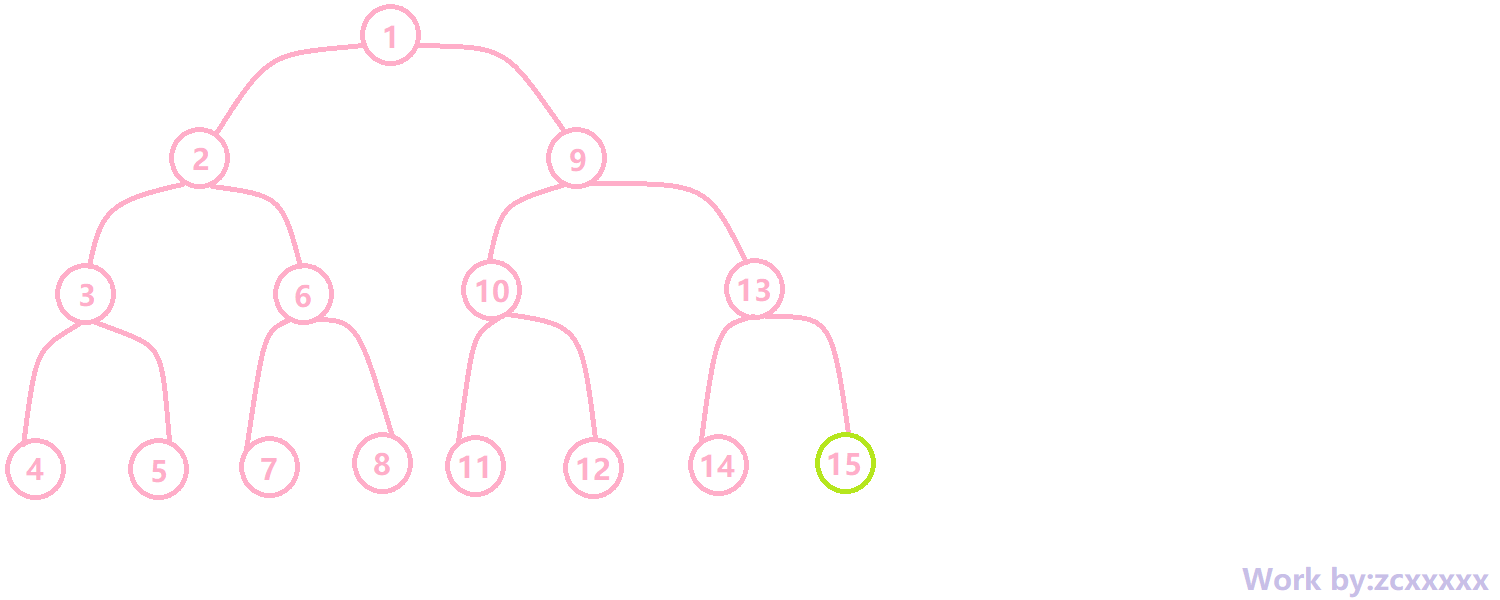
如 \(page2\) ，假设我们要改动的数是图中绿色节点，按照我们之前的说法，需要改的重新建，不要改的连到之前的那个节点上。

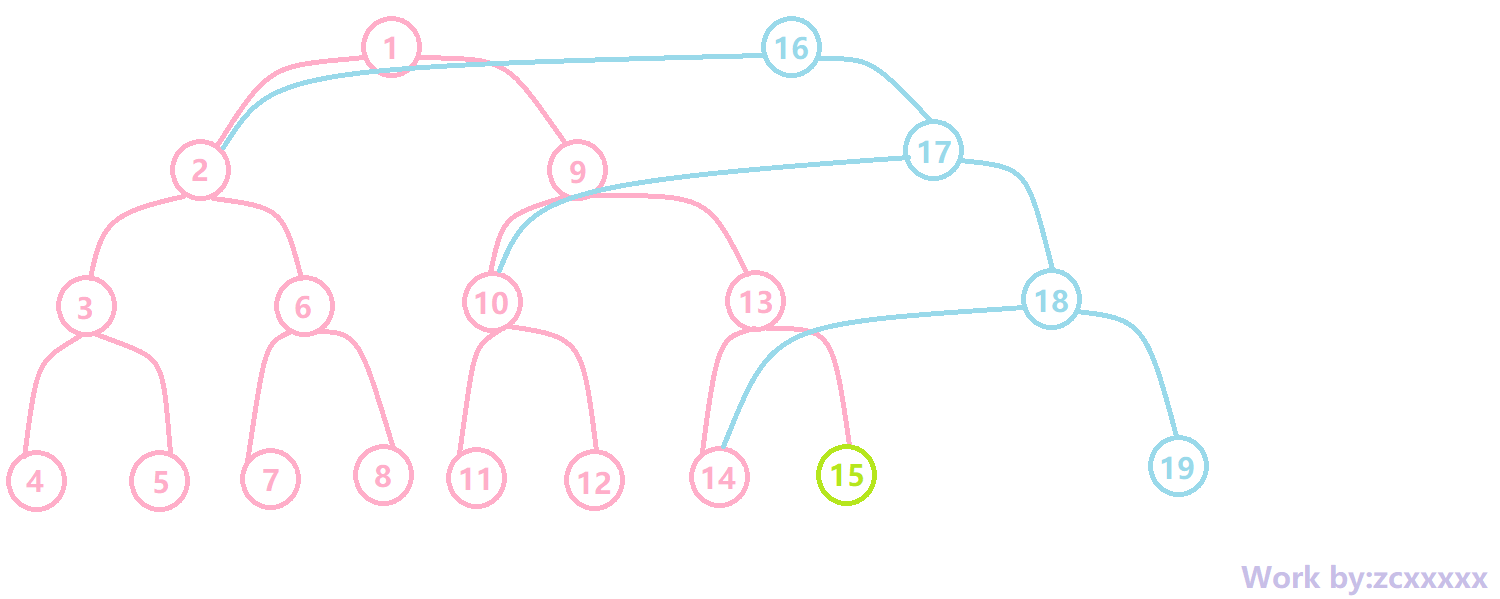
如 \(page3\) ，就改成了这样一个图，挺好理解了吧。

如下是最普通的可查询历史某位置的值的主席树\(code\)

代码挺简单的，跟线段树差不多，就是每次来到一个要改的地方要新建节点。

BOOM！！

/**
 *	author: zcxxxxx
 *	creater: 2022.6.8
**/
#include <bits/stdc++.h>
#define il inline
#define reg register
#define ll long long
//#define int unsigned long long
#define pii pair<int, int>
#define eps 1e-8
using namespace std;
const int A = 1e2 + 7;
const int B = 1e3 + 7;
const int C = 1e4 + 7;
const int D = 6e5 + 7;
const int E = 1e6 + 7;
const int F = 1e7 + 7;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
ll Gcd(ll num1, ll num2) {return !num2 ? num1 : Gcd(num2, num1 % num2);}
ll tx, ty, tz; void Exgcd(ll num1, ll num2) {if(num2 == 0) {tx = 1, ty = 0; return;}
	Exgcd(num2, num1 % num2), tz = tx, tx = ty, ty = tz - num1 / num2 * ty;}
/*General solution: tx += num2 / gcd * k, ty += num1 / gcd * k, k belong to Z*/
ll Gmul(ll x, ll y) {ll ans = 0; while(y != 0) {if(y & 1) ans = (ans + x) % mod; x = (x + x) % mod, y >>= 1;} return ans;}
ll Gpow(ll base, ll pow) {ll ans = 1;while(pow) {if(pow & 1) ans = Gmul(ans, base); base = Gmul(base, base);pow >>= 1;} return ans;}
ll Qpow(ll base, ll pow) {ll ans = 1;while(pow) {if(pow & 1) ans = (ans * base) % mod; base = (base * base) % mod;pow >>= 1;} return ans;}
inline int read() {register int x = 0, t = 1; register char ch = getchar();
while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar(); if(ch == '-') {t = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {x = x * 10 + ch - 48; ch = getchar();}return x * t;}
bool cmpstb(ll a, ll b) {return a < b;}
/*----------------------------------------*/

int n, m;
int top = 0;
int a[D * 40], root[D * 40];
struct node_ {
	int l, r;
	int val;
}t[D * 40];
int clone(int now) {
	++ top;
	t[top] = t[now];
	return top;
}
int build(int now, int l, int r) {
	now = ++ top;
	if(l == r) {
		t[now].val = a[l];
		return top;
	}
	int mid = l + r >> 1;
	t[now].l = build(t[now].l, l, mid);
	t[now].r = build(t[now].r, mid + 1, r);
	return now;
}
int update(int now, int l, int r, int x, int c) {
	now = clone(now);
	if(l == r) {
		t[now].val = c;
	}
	else {
		int mid = l + r >> 1;
		if(x <= mid) t[now].l = update(t[now].l, l, mid, x, c);
		else t[now].r = update(t[now].r, mid + 1, r, x, c);
	}
	return now;
}
int query(int now, int l, int r, int x) {
	if(l == r) {
		return t[now].val;
	}
	int mid = l + r >> 1;
	if(x <= mid) return query(t[now].l, l, mid, x);
	else return query(t[now].r, mid + 1, r, x);
}
signed main() {
	n = read(), m = read();
	for(int i = 1; i <= n; ++ i) a[i] = read();
	root[0] = build(0, 1, n);
	for(int rt, opt, x, y, i = 1; i <= m; ++ i) {
		rt = read(), opt = read(), x = read();
		if(opt == 1) {
			y = read();
			root[i] = update(root[rt], 1, n, x, y);
		}
		else {
			printf("%d\n", query(root[rt], 1, n, x));
			root[i] = root[rt];
		}
	}
	return 0;
}

来套一下权值线段树吧 \(qwq\) Link