欧几里得
引入
123456789x+1=11y,求整数解qwq
这道题其实是初等数论里的线性丢番图方程,即二元一次不定方程,当a,b,c∈Z,求x和y的整数解
求解这个问题要学习辗转相除法
最大公约数(gcd)
求最大公约数的方法有很多种,其中最简单的一种就是质因数分解
我们把两个数分解质因子,当中相同的质因子的乘积就是gcd
先把24和60分解质因子:
所以可得到
这个方法虽然简单,但是在处理较大数的时候很麻烦
所以我们要学习新的方法
辗转相除法
方法:gcd(a, b) = gcd(b, a mod b)
两个数的最大公约数等于其中较小的数字和二者之间余数的最大公约数
过程:
对于161和126
首先较小的126不能整除161
所以126不是最大公约数
因此我们要找一个更小的数,去同时整除126和161
这个地方161可以拆解成126和35
所以我们只要找到126和35的最大公约数就是161和126的最大公约数,下面同理
当最后余数为0的时候,除数 (7) 即为最大公约数
用“gcd”写下来,长这个样
现在只是会用这个方法了,那怎么证明呢?
证明
既然这个算法叫做欧几里得算法,那么我们就回到欧几里得的经典著作,《几何原本》
书中使用线段度量的方法解释的,其中的公度数就是公约数

就是有两个数字,把他变成两条数字长度的线段,然后用较短的线段去度量较长的线段,如果能够量尽(指长线段长度是短线段的倍数,也就是用短线段去丈量长线段,最终没有剩余的线段),由于短线段本身就能把自己量尽,所以短线段这个时候就是两线段长度的最大公约数。
要是量不尽呢,这个时候就需要找一个线段,这个线段需要同时能够量尽126和35。
因为能够量尽126和35,那必然能量尽两者的长度之和,也就是最开始的161。
那问题就被转化成了对126和余下的35找一个最大的公度数。
我们可以重复上边的做法
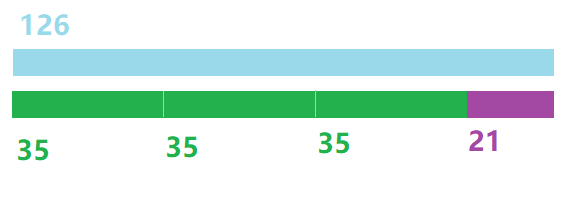
需要继续找到一个线段,能够同时量尽35和11,那他就能够量尽3×35+21,也就是126,再回到上边那一层,他也能量尽126和35还有161
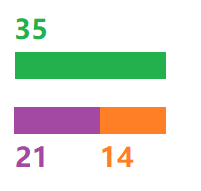
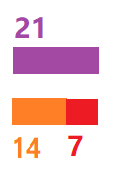

最终,得到7这个数字,从下往上看,7正好整除14,整除14+7=21,整除21+14=35,整除35×3+21=126,整除126+35=161。
我们现在得到的7只知道他是能量尽161和126
但是我们没有证明7是161和126的最大公度数
证明如下:
我们设G为一个正好整除161和126的数,且G>7
要量尽161和126,要先量尽35,要量尽126和35,要先量尽21,要先量尽14,要先量尽7,因为G可以量尽7所以他要小于等于7,但是已有条件G>7就不满足了,所以不存在G,所以7位126和161的最大公度数,也就是我们要求的最大公约数。
欧几里得牛逼!!!
还可以用一个填补正方形的方法理解欧几里得。
不整理了qwq
接下来证明一下
其中r表示a除以b的余数,可记为r = a - kb,k为满足条件的特定整数。
对于a和b的任意一个公约数c,可记为a = pc和b=qc,则
由于k,p,q都是特定整数,说明c也能整除r,因此c也是b和r的公约数。
反着证:
对于b和r的任意一个公约数d,可记为b=xd和r=yd,则
由于k,x,y都是特定整数,说明d也能整除a,因此d也是a和b的公约数。
既然前后的公约数都相等,那么最大公约数也相等
所以 $$gcd(a,b)=gcd(b,r_0)=gcd(r_0,r_1)=......=gcd(r_{n-1},r_n)=gcd(r_{n-1},0)=r_{n-1}$$
这个过程一定会终止,因为每次操作的余数都在减小,且不可能为负数,所以一定存在某一步的时候余数为0
如果两个数不全为整数,那这个过程会终止吗?
这样的话我们需要找
这样每次辗转相除后比例都不变,所以会一直持续下去
想知到裴蜀定理吗,请听下回分解qwq


