Splay

来总结一下调了一整天的 \(Splay\) \(qnq\)

在学习Splay之前，可以先学一下二叉搜索树和Treap。

为什么要学习 \(Splay\)

Splay是通过不断的暴力旋转，将调用某些点时的复杂度大大降低，而且旋转之后其他点的深度最多增加2，所以学一下Splay是很有必要的qwq。

另外以后可能要学 \(LCT\) 之类的东西，现在顺便学了以后方便很多

Splay 是一种用于解决区间问题的数据结构，而不是像普通 Treap 一样只能维护权值的（可能也能维护，但我不会 qwq）

与它相似的还有 FHQ Treap，打算理解了Splay之后再去学学它。

进入正题

这篇博客主要总结一下Splay的旋转技巧和其中的一些问题

Splay是平衡树的一种，中文名为伸展树，由丹尼尔·斯立特Daniel Sleator和罗伯特·恩卓·塔扬Robert Endre Tarjan在1985年发明的

Tarjan orz%%%

它的主要思想是：对于查找频率较高的节点，使其处于离根节点相对较近的节点。

这样就可以保证了查找的效率

保持高效的原因是他能旋转

Splay的旋转与普通Treap不同的是，普通Treap只能转一下，Splay能来好几下，还能直接给你转到根qwq

这也就是Splay比Treap快的地方，而且Splay不需要随机数进行维护

他怎么旋转呢？

先随便口胡一下：

我们设x的父亲为y，y的父亲为z，s是x的某个儿子，这个儿子是左儿子还是右儿子取决于x是y的左儿子还是右儿子，如果x是y的左儿子，那s是x的右儿子，否则反之。

想象一下，把所有点之间的边拆开，将z与x相连，x与y相连，y与s相连，就变成了一颗新树，这时候x的深度降低了！！就达到了旋转的目的，具体怎么转，可以通过画图和代码理解

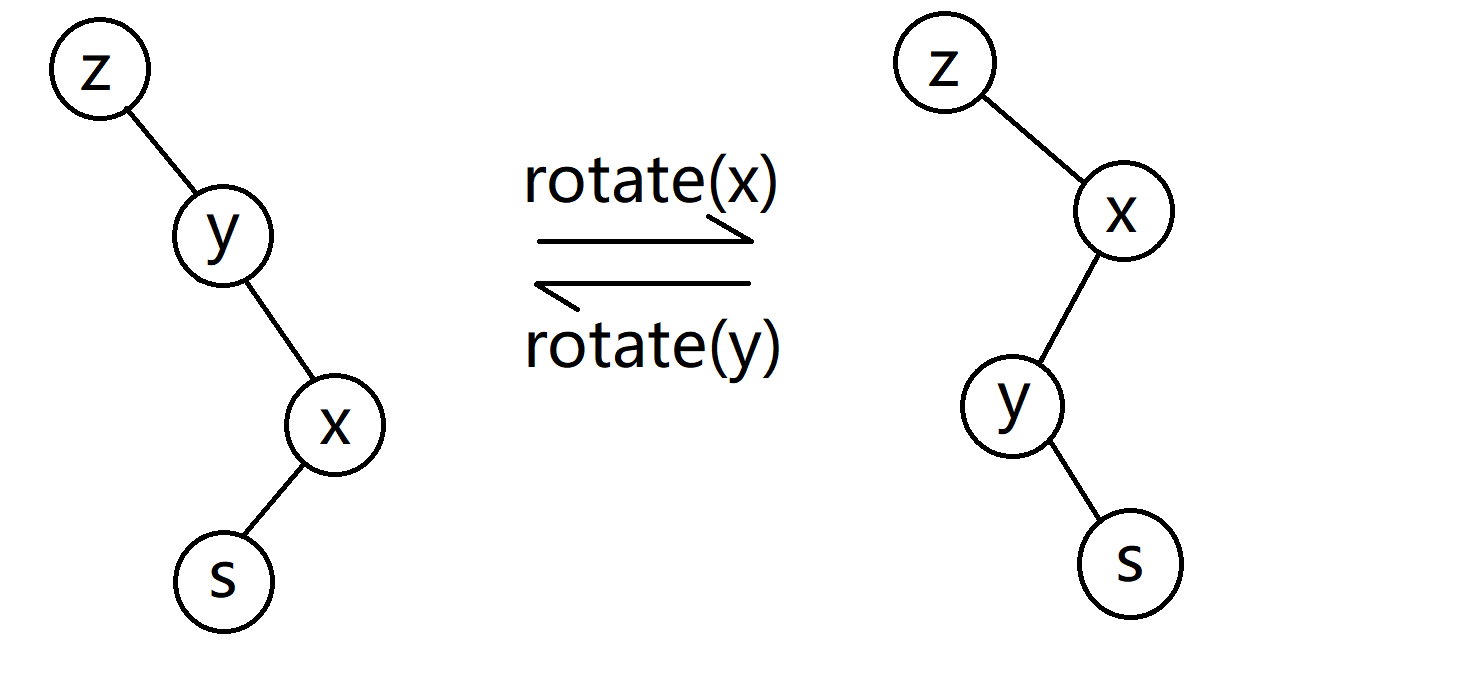
void rotate(int x)
{
	int y = t[x].fa; 
	int z = t[y].fa;
	int k = t[y].son[1] == x; // 判断x为y的左儿子(0)还是右儿子(1)
	t[z].son[t[z].son[1] == y] = x;
	t[x].fa = z;
	// 连接x与z 
	t[y].son[k] = t[x].son[k ^ 1];
	t[t[x].son[k ^ 1]].fa = y;
	// 连接x的儿子与y 
	t[x].son[k ^ 1] = y;
	t[y].fa = x;
	// 连接x与y 
	pushup(y);
	pushup(x);
	// 这里要先合并y，在合并x，因为y变成了x的儿子 
}

我们的Splay旋转不能一次旋一下

因为你会被卡朝

所以我们可以一次旋两下或者更多下（自己发明），这样效率会快一倍。

但是如果我们一味的往上一次旋两下，那肯定是不对的，因为深度不一定是偶数倍嘛。

所以分为一下三种情况：

1. to是x的父亲
   就直接单旋上去就欧克，没什么技巧

2. x和他的父亲在同一边
   啥意思呢，我们在上边设过了y和z

所以就是说x和y同时是y和z的左儿子或者右儿子时

先rotate(y)再rotate(x)

3. x与他的父亲不在同一边

旋转两次x

代码如下

inline void splay(int x, int goal) {
	while(t[x].fa != goal) { // 旋转 
		int y = t[x].fa;
		int z = t[y].fa;
		if(z != goal) {
			(t[y].son[0] == x) ^ (t[z].son[0] == y) ? rotate(x) : rotate(y);
			// ? 前边这些是判断x与y是不是同属于其父亲的左儿子或者右儿子 
		}
		rotate(x);
		// 如果他的grandfather即z已经是目标节点了，只旋转一次x
		// 如果x与y同属一边，先旋转父亲y，在旋转儿子x 
	}
	if(goal == 0) root = x; // 如果他的目标节点是根，那在旋转结束后，root就变成了x 
}