平衡树
treap
首先每个点有键值和优先级
键值为节点本身的权值,优先级为每个节加入时所赋予的随机权值
对于树上一个节点左儿子的键值小于本节点的键值小于右节点的键值,对于键值来说是一颗二叉查找树
对于优先级来说一个节点的优先级要大于它的两个儿子的优先级,本质上是一个大根堆,用随机权值赋值是用来使深度接近log的
FHQ
Split 操作
将一颗树按照左树所有键值小于等于 x,右树所有键值大于 x 进行分裂
考虑当考虑到 u 节点,当 u 节点键值小于等于 x 时,它的左树和它都应该接在左树上,然后往右子树递归
反之,则右子树和它接在右子树上,然后往左子树递归
这里我们传一个 L 和 R 的指针,L 这里放的是左树如果想要添加节点应该接在 L 这个位置,R 这里放的是右树如果想要添加节点应该接在 R 这个位置
然后只要将 L=u 或 R=u 就能将 u 节点接在左/右子树了
代码:
void Split(int u,int x,int &L,int &R){
if(u==0){
L=R=0;
return;
}
if(tr[u].key<=x){
L=u;
Split(tr[u].rs,x,tr[u].rs,R);
}
else{
R=u;
Split(tr[u].ls,x,L,tr[u].ls);
}
Update(u);
}
merge 操作
将两颗平衡树合并成一颗,首先分裂出的 L 和 R 分别表示左树的根和右树的根
此时合并需要满足优先值大的在优先值小的上面,所以我们比较两个子树的根决定谁在上谁在下
然后再返回其的根
int Merge(int L,int R){
if(L==0||R==0) return L+R;
if(tr[L].pri>tr[R].pri){
tr[L].rs=Merge(tr[L].rs,R);//左子树的右儿子和右子树合并
Update(L);
return L;
}
else{
tr[R].ls=Merge(L,tr[R].ls);
Update(R);
return R;
}
}
其它操作
加点
将平衡树按照键值 x 分裂成两颗,再分别合并
删点
将平衡树分裂成键值 <x ,=x ,>x 三颗
然后将 =x 子树的根去掉(即将子树的左右儿子合并成新的子树)
然后再依次合并各个子树
查排名
将子树分成 <=x-1 和 >x-1 两颗,然后查询左子树大小
区间第 k 大
根据二叉树性质,然后通过子树大小查询,递归实现,建议结合代码理解
int Kth(int u,int k){
if(tr[tr[u].ls].siz+1==k) return u;
if(tr[tr[u].ls].siz>=k) return Kth(tr[u].ls,k);
if(tr[tr[u].ls].siz<k) return Kth(tr[u].rs,k-tr[tr[u].ls].siz-1);
}
前驱
求比 x 小的最大的数
通过将子树分裂成 <=x-1 和 >x-1 然后在左子树中通过区间第 k 大实现
后继
求比 x 大的最小的数
与前驱同理
模板代码(P3369)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=1e6+5;
int n,root,cnt;
struct Node{
int ls,rs,key,pri,siz;
}tr[M];
void newNode(int x){
cnt++;
tr[cnt]={0,0,x,rand(),1};
}
void Update(int u){
tr[u].siz=tr[tr[u].ls].siz+tr[tr[u].rs].siz+1;
}
void Split(int u,int x,int &L,int &R){
if(u==0){
L=R=0;
return;
}
if(tr[u].key<=x){
L=u;
Split(tr[u].rs,x,tr[u].rs,R);
}
else{
R=u;
Split(tr[u].ls,x,L,tr[u].ls);
}
Update(u);
}
int Merge(int L,int R){
if(L==0||R==0) return L+R;
if(tr[L].pri>tr[R].pri){
tr[L].rs=Merge(tr[L].rs,R);
Update(L);
return L;
}
else{
tr[R].ls=Merge(L,tr[R].ls);
Update(R);
return R;
}
}
void Insert(int x){
int L,R;
Split(root,x,L,R);
newNode(x);
root=Merge(Merge(L,cnt),R);
}
void Del(int x){
int L,R,p;
Split(root,x,L,R);
Split(L,x-1,L,p);
p=Merge(tr[p].ls,tr[p].rs);
root=Merge(Merge(L,p),R);
}
void Rank(int x){
int L,R;
Split(root,x-1,L,R);
printf("%d\n",tr[L].siz+1);
Merge(L,R);
}
int Kth(int u,int k){
if(tr[tr[u].ls].siz+1==k) return u;
if(tr[tr[u].ls].siz>=k) return Kth(tr[u].ls,k);
if(tr[tr[u].ls].siz<k) return Kth(tr[u].rs,k-tr[tr[u].ls].siz-1);
}
void Pre(int x){
int L,R;
Split(root,x-1,L,R);
printf("%d\n",tr[Kth(L,tr[L].siz)].key);
root=Merge(L,R);
}
void Suc(int x){
int L,R;
Split(root,x,L,R);
printf("%d\n",tr[Kth(R,1)].key);
root=Merge(L,R);
}
int main(){
srand(time(NULL));
scanf("%d",&n);
for(int i=1;i<=n;i++){
int op,x;
scanf("%d%d",&op,&x);
if(op==1) Insert(x);
if(op==2) Del(x);
if(op==3) Rank(x);
if(op==4) printf("%d\n",tr[Kth(root,x)].key);
if(op==5) Pre(x);
if(op==6) Suc(x);
}
}
按排名分裂(P4008)
每个节点不一定需要有键值,当我们要维护一个序列,支持插入和删除时,我们需要将平衡树上维护一个排名来确定这个结点所在序列上的位置,而这个这个排名可以通过维护它的中序来得到
所以我们只需要修改 Split 函数,使左树的结点个数等于 x
这样这道题就转化为模板题了
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=4e6+5;
int T,cnt,root,pos;
char op[100];
struct Node{
char val;
int ls,rs,pri,siz;
}tr[N];
void newNode(char val){
cnt++;
tr[cnt]={val,0,0,rand(),1};
}
void Update(int u){
tr[u].siz=tr[tr[u].ls].siz+tr[tr[u].rs].siz+1;
}
void Split(int u,int x,int &L,int &R){
if(u==0){
L=R=0;
return;
}
if(tr[tr[u].ls].siz+1<=x){
L=u;
Split(tr[u].rs,x-tr[tr[u].ls].siz-1,tr[u].rs,R);
}
else{
R=u;
Split(tr[u].ls,x,L,tr[u].ls);
}
Update(u);
}
int Merge(int L,int R){
if(L==0||R==0) return L+R;
if(tr[L].pri>tr[R].pri){
tr[L].rs=Merge(tr[L].rs,R);
Update(L);
return L;
}
else{
tr[R].ls=Merge(L,tr[R].ls);
Update(R);
return R;
}
}
void inorder(int u){
if(u==0) return;
inorder(tr[u].ls);
printf("%c",tr[u].val);
inorder(tr[u].rs);
}
int main(){
srand(time(NULL));
scanf("%d",&T);
while(T--){
scanf("%s",op+1);
if(op[1]=='M') scanf("%d",&pos);
if(op[1]=='I'){
int L,R,len;
scanf("%d",&len);
Split(root,pos,L,R);
for(int i=1;i<=len;i++){
char c;
scanf("%c",&c);
while(c<32||126<c) scanf("%c",&c);
newNode(c);
L=Merge(L,cnt);
}
root=Merge(L,R);
}
if(op[1]=='D'){
int L,R,p,len;
scanf("%d",&len);
Split(root,pos,L,R);
Split(R,len,p,R);
root=Merge(L,R);
}
if(op[1]=='G'){
int L,R,p,len;
scanf("%d",&len);
Split(root,pos,L,R);
Split(R,len,p,R);
inorder(p);
root=Merge(L,Merge(p,R));
printf("\n");
}
if(op[1]=='P') pos--;
if(op[1]=='N') pos++;
}
}
P3391 【模板】文艺平衡树
需要对序列进行区间翻转操作,求最后翻转完的序列
首先我们先将序列添加到 treap 上
观察下图:
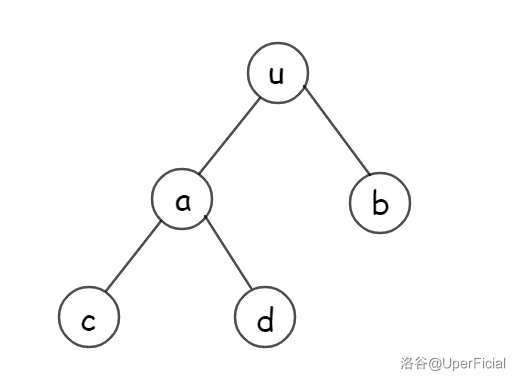
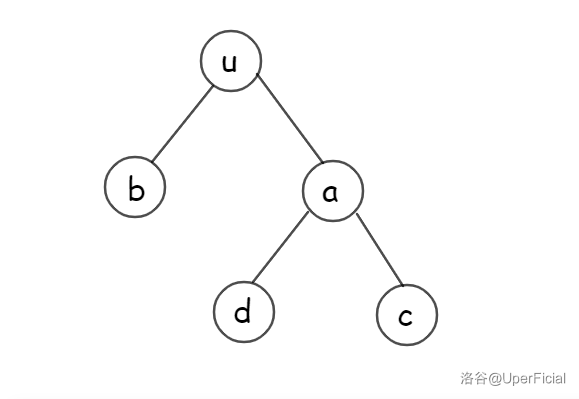
它翻转一个子树的操作就相当与不断交换每个非叶子结点的左右儿子,可以手模一下,非常巧妙
所以我们有一种暴力的思想就是每一次交换操作先将区间所对应的子树分裂出来,然后暴力的进行交换操作
但是复杂度肯定不对,我们考虑什么时候一个节点的左右儿子会变,只有在对它的左右儿子进行合并或查询时才会改变,并且都是从上到下递归实现
所以考虑类似于线段树的懒标记,我们先在需要翻转的区间的根打上标记,当访问到根的时候就把标记下传,就可以在修改树的结构之前先进行翻转了
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,root,cnt;
struct Node{
int ls,rs,val,pri,tag,siz;
}tr[N];
void newNode(int x){
++cnt;
tr[cnt]={0,0,x,rand(),0,1};
}
void Update(int u){
tr[u].siz=tr[tr[u].ls].siz+tr[tr[u].rs].siz+1;
}
void Pushdown(int u){
if(!tr[u].tag) return;
swap(tr[u].ls,tr[u].rs);
tr[tr[u].ls].tag^=1;
tr[tr[u].rs].tag^=1;
tr[u].tag=0;
}
void Split(int u,int x,int &L,int &R){
if(u==0){
L=R=0;
return;
}
Pushdown(u);
if(tr[tr[u].ls].siz+1<=x){
L=u;
Split(tr[u].rs,x-tr[tr[u].ls].siz-1,tr[u].rs,R);
}
else{
R=u;
Split(tr[u].ls,x,L,tr[u].ls);
}
Update(u);
}
int Merge(int L,int R){
if(L==0||R==0) return L+R;
if(tr[L].pri>tr[R].pri){
Pushdown(L);
tr[L].rs=Merge(tr[L].rs,R);
Update(L);
return L;
}
else{
Pushdown(R);
tr[R].ls=Merge(L,tr[R].ls);
Update(R);
return R;
}
}
void Insert(int x){
newNode(x);
root=Merge(root,cnt);
}
void inorder(int u){
if(u==0) return;
Pushdown(u);
inorder(tr[u].ls);
printf("%d ",u);
inorder(tr[u].rs);
}
int main(){
srand(time(NULL));
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
Insert(i);
}
for(int i=1;i<=m;i++){
int l,r;
scanf("%d%d",&l,&r);
int L,R,p;
Split(root,r,L,R);
Split(L,l-1,L,p);
tr[p].tag^=1;
root=Merge(Merge(L,p),R);
}
inorder(root);
}
P2042 [NOI2005] 维护数列
一道细节很多的很好的平衡树练习题
考虑上一道题给我们的启示是什么:就是线段树的结构和平衡树非常相似,所以我们可以直接照搬线段树上的操作到平衡树上来
看这道题的操作:加入删除都是平衡树板子,区间覆盖区间求和区间求最大字段和都是线段树可以维护的东西,区间翻转更是由线段树的懒标记操作引申到文艺平衡树上的
所以我们依旧使用线段树的思想,最大字段和记录区间内最长和区间左开右闭,左闭右开最长的三种情况,拼接到一起,然后区间覆盖操作对于根的位置打上懒标记,下传时顺便修改以下区间和区间 max 这之类的就行
此外,还要注意空间问题,我们一个一个点开需要 4e6 会炸,但是一个数列中至多只有 5e5 个数,我们可以回收空间,删除掉的结点放入栈,每一次从栈中取出结点编号即可
另外有一个小优化,建树时一个一个加点是很慢的,我们可以递归加点就是把加点的顺序改成树的形式递归,可以节省一个 log,底下这篇题解有讲
细节很多,这篇题解 讲的非常详细
代码(在htc大佬的帮助下,终于调过了):
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+5;
int n,m,stl=1,str=0,root;
int st[N],a[N];
struct Node{
int ls,rs,val,pri,siz,tag,mx,mx1,mx2,ch,sum;
}tr[N];
void operation(){
srand(time(NULL));
for(int i=1;i<=5e5;i++){
st[++str]=i;
}
}
int newNode(int x){
int id=st[stl++];
tr[id]={0,0,x,rand(),1,0,x,max(x,0ll),max(x,0ll),0,x};
return id;
}
void Update(int u){
int ls=tr[u].ls,rs=tr[u].rs;
tr[u].siz=tr[ls].siz+tr[rs].siz+1;
tr[u].sum=tr[ls].sum+tr[rs].sum+tr[u].val;
tr[u].mx1=max({tr[ls].mx1,tr[ls].sum+tr[u].val+tr[rs].mx1,0ll});
tr[u].mx2=max({tr[rs].mx2,tr[rs].sum+tr[u].val+tr[ls].mx2,0ll});
tr[u].mx=max(tr[ls].mx2+tr[rs].mx1,0ll)+tr[u].val;
if(ls) tr[u].mx=max(tr[u].mx,tr[ls].mx);
if(rs) tr[u].mx=max(tr[u].mx,tr[rs].mx);
}
void Reverse(int u){
swap(tr[u].ls,tr[u].rs);
swap(tr[u].mx1,tr[u].mx2);
tr[u].tag^=1;
}
void Cover(int u,int z){
tr[u].val=z;
tr[u].sum=tr[u].siz*z;
tr[u].mx1=max(0ll,tr[u].sum);
tr[u].mx2=max(0ll,tr[u].sum);
tr[u].mx=max(tr[u].val,tr[u].sum);
tr[u].ch=1;
}
void Pushdown(int u){
if(tr[u].tag){
Reverse(tr[u].ls);
Reverse(tr[u].rs);
tr[u].tag=0;
}
if(tr[u].ch){
Cover(tr[u].ls,tr[u].val);
Cover(tr[u].rs,tr[u].val);
tr[u].ch=0;
}
}
void Try(int u){//调试输出函数
if(u==0) return;
Pushdown(u);
Try(tr[u].ls);
printf("%lld ",tr[u].val);
Try(tr[u].rs);
}
void Split(int u,int x,int &L,int &R){
if(u==0){
L=R=0;
return;
}
Pushdown(u);
if(tr[tr[u].ls].siz+1<=x){
L=u;
Split(tr[u].rs,x-tr[tr[u].ls].siz-1,tr[u].rs,R);
}
else{
R=u;
Split(tr[u].ls,x,L,tr[u].ls);
}
Update(u);
}
int Merge(int L,int R){
if(L==0||R==0) return L+R;
if(tr[L].pri>tr[R].pri){
Pushdown(L);
tr[L].rs=Merge(tr[L].rs,R);
Update(L);
return L;
}
else{
Pushdown(R);
tr[R].ls=Merge(L,tr[R].ls);
Update(R);
return R;
}
}
int Add(int l,int r){
if(l!=r){
int mid=(l+r)>>1;
return Merge(Add(l,mid),Add(mid+1,r));
}
return newNode(a[l]);
}
void Insert(int pos,int tot){
int L,R;
Split(root,pos,L,R);
for(int i=1;i<=tot;i++){
scanf("%lld",&a[i]);
}
root=Merge(Merge(L,Add(1,tot)),R);
// Try(root);
// printf("\n");
}
void rmv(int u){
if(stl>1) st[--stl]=u;
else st[++str]=u;
if(tr[u].ls) rmv(tr[u].ls);
if(tr[u].rs) rmv(tr[u].rs);
}
void Delete(int pos,int tot){
int L,R,p;
Split(root,pos+tot-1,L,R);
Split(L,pos-1,L,p);
rmv(p);
root=Merge(L,R);
// Try(root);
// printf("\n");
}
void Change(int pos,int tot,int z){
int L,R,p;
Split(root,pos+tot-1,L,R);
Split(L,pos-1,L,p);
Cover(p,z);
root=Merge(Merge(L,p),R);
// Try(root);
// printf("\n");
}
void Longreverse(int pos,int tot){
int L,R,p;
Split(root,pos+tot-1,L,R);
Split(L,pos-1,L,p);
Reverse(p);
root=Merge(Merge(L,p),R);
// Try(root);
// printf("\n");
}
void Longquery(int pos,int tot){
int L,R,p;
Split(root,pos+tot-1,L,R);
Split(L,pos-1,L,p);
printf("%lld\n",tr[p].sum);
root=Merge(Merge(L,p),R);
}
void Paraquery(){
Update(root);
printf("%lld\n",tr[root].mx);
}
signed main(){
operation();
scanf("%lld%lld",&n,&m);
Insert(0,n);
for(int i=1;i<=m;i++){
char op[20];
int pos,tot,c;
scanf("%s",op);
if(op[0]=='I'){
scanf("%lld%lld",&pos,&tot);
Insert(pos,tot);
}
if(op[0]=='D'){
scanf("%lld%lld",&pos,&tot);
Delete(pos,tot);
}
if(op[0]=='M'&&op[2]=='K'){
scanf("%lld%lld%lld",&pos,&tot,&c);
Change(pos,tot,c);
}
if(op[0]=='R'){
scanf("%lld%lld",&pos,&tot);
Longreverse(pos,tot);
}
if(op[0]=='G'){
scanf("%lld%lld",&pos,&tot);
Longquery(pos,tot);
}
if(op[0]=='M'&&op[2]=='X'){
Paraquery();
}
}
}
P2596 [ZJOI2006] 书架
我们要用 FHQ 维护一个序列,使得知道其在序列中的下标可以知道它的编号,知道其编号可以确定其在序列中的下标
考虑首先先用 FHQ 把序列按照中序存储,经典套路
然后我们考虑当知道了一个点的编号后,就可以知道它维护了那些东西,我们要是想知道这个点在中序中的什么位置,就要一直跳到根节点,在它一直跳父亲的过程中统计答案
所以就对于一个节点多维护一个父亲,考虑在跳的时候只有右儿子往父亲跳的时候有贡献,所以再维护它是左儿子还是右儿子
然后注意一些细节:如结点最开始在的位置的左儿子也有贡献,根节点在上传时不会被更新是左儿子还是右儿子,要特殊考虑,细节自己实现
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=8e4+5;
int n,m,root;
struct Node{
int ls,rs,siz,fa,op,pri;
}tr[N];
void Operation(){
srand(time(NULL));
}
void newNode(int x){
tr[x]={0,0,1,0,0,rand()};
}
void Update(int u){
tr[u].siz=tr[tr[u].ls].siz+tr[tr[u].rs].siz+1;
tr[u].op=0;
tr[tr[u].ls].fa=u;tr[tr[u].rs].fa=u;
tr[tr[u].ls].op=0;tr[tr[u].rs].op=1;
}
int inv(int u,int x){
if(u==0) return x;
if(tr[u].op==0) return inv(tr[u].fa,x);
return inv(tr[u].fa,x+tr[tr[tr[u].fa].ls].siz+1);
}
int query(int u){
int res=tr[tr[u].ls].siz+1;
return inv(u,0)+res;
}
void Try(int u){
if(u==0) return;
Try(tr[u].ls);
printf("%d ",u);
Try(tr[u].rs);
}
void Split(int u,int x,int &L,int &R){
if(u==0){
L=R=0;
return;
}
if(tr[tr[u].ls].siz+1<=x){
L=u;
Split(tr[u].rs,x-tr[tr[u].ls].siz-1,tr[u].rs,R);
}
else{
R=u;
Split(tr[u].ls,x,L,tr[u].ls);
}
Update(u);
}
int Merge(int L,int R){
if(L==0||R==0) return L+R;
if(tr[L].pri>tr[R].pri){
tr[L].rs=Merge(tr[L].rs,R);
Update(L);
return L;
}
else{
tr[R].ls=Merge(L,tr[R].ls);
Update(R);
return R;
}
}
void Delete(int pos){
int L,R,p;
Split(root,pos-1,L,R);
Split(R,1,p,R);
root=Merge(L,R);
}
void Insert(int pos,int x){
int L,R;
Split(root,pos,L,R);
root=Merge(Merge(L,x),R);
}
int find(int u,int x){
if(tr[tr[u].ls].siz+1==x) return u;
if(tr[tr[u].ls].siz+1<=x) return find(tr[u].rs,x-tr[tr[u].ls].siz-1);
return find(tr[u].ls,x);
}
int main(){
Operation();
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
int p;
scanf("%d",&p);
newNode(p);
Insert(i-1,p);
}
// Try(root);
// printf("\n");
for(int i=1;i<=m;i++){
char op[10];
scanf("%s",op+1);
int s,t;
if(op[1]=='T'){
scanf("%d",&s);
int pos=query(s);
Delete(pos);
Insert(0,s);
}
if(op[1]=='B'){
scanf("%d",&s);
int pos=query(s);
Delete(pos);
Insert(n-1,s);
}
if(op[1]=='I'){
scanf("%d%d",&s,&t);
int pos=query(s);
Delete(pos);
Insert(pos-1+t,s);
}
if(op[1]=='A'){
scanf("%d",&s);
int pos=query(s);
printf("%d\n",pos-1);
}
if(op[1]=='Q'){
scanf("%d",&s);
printf("%d\n",find(root,s));
}
}
}
P3165 [CQOI2014] 排序机械臂
切了,但是调试到崩溃
维护一个序列,支持区间翻转和区间查询最小值
考虑类线段树的标记上下传操作,然后维护懒标记和最小值即可
注:这里有重复的值,且编号小的排在前,所以要离散化重新赋值
注:在查询时也要下传标记
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,root,cnt;
int a[N],num[N],ans[N],b[N];
map<int,int>mp;
struct Node{
int ls,rs,pri,mn,siz,tag,val;
}tr[N];
int newNode(int x){
tr[++cnt]={0,0,rand(),x,1,0,x};
return cnt;
}
void operation(){
srand(time(NULL));
}
void Update(int u){
tr[u].siz=tr[tr[u].ls].siz+tr[tr[u].rs].siz+1;
tr[u].mn=tr[u].val;
if(tr[u].ls) tr[u].mn=min(tr[u].mn,tr[tr[u].ls].mn);
if(tr[u].rs) tr[u].mn=min(tr[u].mn,tr[tr[u].rs].mn);
}
void Pushdown(int u){
if(tr[u].tag){
swap(tr[u].ls,tr[u].rs);
if(tr[u].ls) tr[tr[u].ls].tag^=1;
if(tr[u].rs) tr[tr[u].rs].tag^=1;
tr[u].tag=0;
}
}
void Split(int u,int x,int &L,int &R){
if(u==0){
L=R=0;
return;
}
Pushdown(u);
if(tr[tr[u].ls].siz+1<=x){
L=u;
Split(tr[u].rs,x-tr[tr[u].ls].siz-1,tr[u].rs,R);
}
else{
R=u;
Split(tr[u].ls,x,L,tr[u].ls);
}
Update(u);
}
int Merge(int L,int R){
if(L==0||R==0) return L+R;
if(tr[L].pri>tr[R].pri){
Pushdown(L);
tr[L].rs=Merge(tr[L].rs,R);
Update(L);
return L;
}
else{
Pushdown(R);
tr[R].ls=Merge(L,tr[R].ls);
Update(R);
return R;
}
}
int query(int u,int x,int z){
Pushdown(u);
if(tr[u].val==x) return z+tr[tr[u].ls].siz+1;
if(tr[tr[u].ls].mn==x) return query(tr[u].ls,x,z);
return query(tr[u].rs,x,z+tr[tr[u].ls].siz+1);
}
void Try(int u){
if(u==0) return;
Try(tr[u].ls);
printf("%d ",tr[u].val);
Try(tr[u].rs);
}
int change(int x){
int pos=query(root,x,0);
int L,R,p;
Split(root,pos,L,R);
Split(L,pos-1,L,p);
tr[L].tag^=1;
root=Merge(L,R);
return pos;
}
int main(){
operation();
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
b[i]=a[i];
}
sort(b+1,b+1+n);
for(int i=1;i<=n;i++){
if(!mp[b[i]]) mp[b[i]]=i;
}
for(int i=1;i<=n;i++){
a[i]=mp[a[i]]++;
}
for(int i=1;i<=n;i++){
root=Merge(root,newNode(a[i]));
}
for(int i=1;i<=n;i++){
ans[i]=i+change(i)-1;
}
for(int i=1;i<=n;i++){
printf("%d ",ans[i]);
}
}
练习题
P3224
P2161
P1110
P2286
P1486
P3165



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· NetPad:一个.NET开源、跨平台的C#编辑器
· PowerShell开发游戏 · 打蜜蜂
· 凌晨三点救火实录:Java内存泄漏的七个神坑,你至少踩过三个!