信息学奥赛一本通汇总

「基础算法」

第1章 递推算法

博客链接

总结：

1. 一般有具体的情境，可以通过直接的模拟转移过程来实现递推，T2，T4，T9
2. 找到已知状态和所求状态的差别和联系，想办法将所求转化为已知进行转移，一般要用到分讨，T1，T3
3. 根据题目将问题转化，增维，然后转化后进行递推，T8

第2章 贪心算法

博客链接

总结：

1. 一般像题目说什么全部都要满足，然后求最小代价这类题目是贪心，T1，T2，T3，T5，T6 若是什么选择一部分，获得最大代价，那么大抵可以往dp，反悔贪心上考虑
2. 还有一类题型，有很多权值，每一个权值都可以选择不同的代价，所以肯定是权值最小的选最大的代价更优，经典模型，哈夫曼树，汽车匹配加油站模型，T4
3. 字典序很容易出贪心，可能每次取最大值的本质注定它是个贪心吧，T7
4. 根据运算的性质选择贪心方式，比如T8，或越或越多，与越与越少，于是就能决定贪心选择的长度
5. 经典套路，每个物品代价相同，影响不同，所以每次贪心选择影响最小的物品更优T9

第3章 二分算法

博客链接

总结：

1. 典中典，最大值最小问题，T1
2. 可以清晰的把数列分成一个具有单调性的问题，常见有奇偶，T2
3. 答案为一个值，还有另外一个条件，求满足这个条件下值的最大（最小）值，因为条件不好搞，并且这个值具有单调性，只有满足条件和不满足条件这两种状态，于是就将求值问题转化为了给定值判断是否合法问题，T3，T4，T5，T6，T7，T8

第4章 深度搜索

博客链接

1. 直接按照题目限制和要传递的变量搜索即可，T1，T2
2. 剪枝技巧1：当正确答案有且仅有一个时，对于枚举顺序的优化可以使得枚举次数变少，T3，T4
3. 剪枝技巧2：可行性剪枝，一种方案如果枚举到一半已经不合法了，就去掉，T3
4. 剪枝技巧3：上下界剪枝，对于枚举时做出的优化，根本不枚举一些本就不合法的枚举，常搭配数学技巧，T4
5. 剪枝技巧4：最优性剪枝，因为当我们求出来一个答案后，如果后面搜索到的结果已经不具备比这个答案优的可能了的话，就剪掉好了，通常可以搭配上枚举顺序的优化
6. 折半搜索，对于需要在一个序列中选出一些数然后来满足一个条件的问题，我搜一半，就可以直接判断另一半中哪一些是合法的，一般n<=40，T4

trick+1：如果是跟约数，因数相关的可以往质因数方面考虑，并且因为小一点的质因数有时具有很好的性质，所以只用枚举在一定范围的约数即可

第5章 广度搜索

博客链接

1. 对于题目中的各种技能(最多用多少次)，不好操作的，可以作为一种状态下传，相当于多了一种转移方式，类似于分层图的思想，T3，T10
2. 对于有多个终点可以建立虚点方便统计答案，T9

边权与bfs和spfa：

知州所众，spfa是最短路算法的一种，一个点可以重复入队，所以会导致复杂度劣于bfs

很关键的一点是因为其边权不固定，所以可能会出现之后遍历到的要比之前更优，就要重新计算了

然而bfs之所以稳定，是因为它只有一种边权，就是1

每次固定在队列里出现的点的深度最多相差1，并且深度小的是排在深度大的前面的，所以每次更新时保证了一定更新的是最优答案，其关键就在于队列里顺序是递增的

并且我们发现在没有负权边时我们只要保证队列里顺序时递增的就可以保证每更新到一个点一定是其的最优解（dij就是这个原理，证明详见最短路）

所以dij也可以理解为将bfs的队列改成优先队列，来保持队列内递增（大雾）

所以当边权有两种例如T4，0/1，我们可以把队列改成双端队列，这样让边权为0的加入在前面，边权为1的加入在后面，这样也可以保证队列的单调性，节省了排序或重复加入队列的复杂度

trick+1：当边权较小时w<=10，然后用最短路容易炸时，我们可以将边权拆点，将一条边拆成若干条边权为1的边和一些点，然后跑bfs即可

spfa相当于是暴力转移，所以大抵适用于所有情况，没有更新顺序，一个点若是被更新了答案，那么只好再次入队更新其他答案

这样就很好理解了

bfs与dfs：

对于具体情景问题的话是一般有固定的用法的：

本人最喜欢用到的还是dfs来解决问题，递归的比较舒服，大部分情况都能胜任

然而只有在图上跑的时候显然dfs是不合适的，这时就要采取bfs

谈一下对于二叉树情况的复杂度：

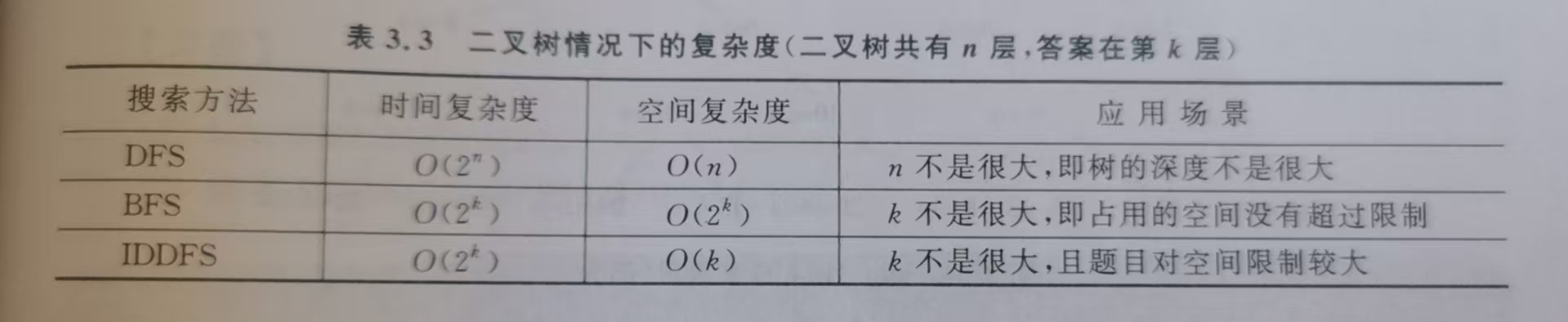
对于这种情况，dfs复杂度过高，bfs空间过曝的情况，可以采用IDA*算法

「字符串算法」

第1章 字符串处理

博客链接

没啥好讲的，只要把字符穿char，string基础搞好就行了

第2章 Hash 和 Hash 表

博客链接

1. 将一堆数或字符串转化为一个数，方便比较，T1，T4，T5，T6，T7，T8，T9，T10
2. 对于回文比较问题，可以通过二分+哈希解决，T2，T3

第3章 KMP 算法

博客链接

1. 因为nxt具有很好的前缀后缀相同的性质，所以有一些限制很奇怪的题，大抵可以往这方面考虑，T2，T3，T6
2. 对于子串问题，显然kmp只能胜任固定一个端点来找另一个端点的工作，所以字串问题只能枚举左端点，然后kmp寻找右端点，T4，T5
3. 把匹配的多维限制转化为一个可以比较的值是很常见的转化方法，我们需要找到其能满足限制所隐含的条件来做文章，T8，T9

第4章 字典树

博客链接

1. 对于在一堆字符串中匹配出前缀这类问题很适用，T1，T4，T5，T6，T8
2. 把一个二进制串看成只包含0/1的字符串，然后进行各种异或问题，就是相当于在树上越远离越好，也非常经典，T2，T3，T7，T9

第5章 AC自动机

博客链接

1. 用于在好多个字符串和一个字符串进行子串比较时使用，T1，T5
2. 对于那种无法保证每个单词的长度的题，我们暴力往上跳会超时，所以需要打上懒标记，然后按照拓扑序上传标记，T2，T3

trick+1：在kmp或AC自动机时之前所匹配的j是适用的可回退的，例T4