数据结构优化dp专题选讲
算法理解
DP的效率取决于三方面：
- 状态总数
- 每个状态的决策数
- 状态转移计算量
对应的优化方式：
- 状态总数的优化：类比搜索剪枝，去除无效的状态；降维，设计dp状态时用低维的dp
- 减少决策数量：状态转移方程的优化，例：四边形不等式优化，斜率优化
- 状态转移计算量优化：用预处理减少地推时间；用hash表，单调队列，线段数，树状数组减少枚举时间
树状数组优化dp
方伯伯的玉米田
戳我查看题解
首先有一个贪心，就是我们要使得单调不降子序列最长，所以显然区间操作的右端点为 \(N\)
考虑正常我们怎么求单调不降子序列，用 \(dp[i]\) 表示以第 \(i\) 个数为结尾的最长不降子序列长度，于是转移就是
\[dp[i]=\max \\\{ dp[j]+1 \\\} , (a[i]>=a[j],j<i)
\]
现在我们可以再加一维状态 \(dp[i][j]\) 表示以第 \(i\) 个数为结尾，并进行了 \(j\) 次 \(+1\) 操作，所能得到的最长不降子序列长度，于是有转移方程
\[dp[i][j]=\max \{ dp[x][y]+1\} ,(y<j,a[i]+j>=a[x]+y)
\]
代码：
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+5,K=505,A=5500;
int n,k;
int a[N],tr[A+5][K],dp[N][K];
int lowbit(int x){
return x&(-x);
}
void add(int x,int y,int z){
for(int i=x;i<=A;i+=lowbit(i)){
for(int j=y;j<=k+1;j+=lowbit(j)){
tr[i][j]=max(tr[i][j],z);
}
}
}
int query(int x,int y){
int res=0;
for(int i=x;i;i-=lowbit(i)){
for(int j=y;j;j-=lowbit(j)){
res=max(res,tr[i][j]);
}
}
return res;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++){
for(int j=0;j<=k;j++){
int mx=query(a[i]+j,j+1);//注：因为树状数组无法接受下标为0的值，要+1
dp[i][j]=mx+1;
}
for(int j=0;j<=k;j++){
add(a[i]+j,j+1,dp[i][j]);//因为转移时y<j，所以要在第i层统计完答案后再添加
}
}
printf("%d",query(A,k+1));//dp[n][k]不一定是最大的答案
}
免费的馅饼
戳我查看题解
观察数据范围，直接确定了我们要在馅饼间转移，考虑设计dp状态 \(dp[i]\) 表示接到第i个馅饼能获得的最大的价值
状转方程
\[dp[i]=\max \\\{ dp[j]+v[i]\\\} ,(\left| p_i-p_j\right|\leq\left| t_i-t_j\right|\times 2)
\]
然后考虑后面的限制条件比较烦人，需要拆绝对值，就把它分两种情况拆掉
当 \(p_i>p_j\) 时，\(2 \times t_i-p_i \geq 2 \times t_j-p_j\)
当 \(p_i\leq p_j\) 时，\(2 \times t_i+p_i \geq 2 \times t_j+p_j\)
我们先预处理出 \(lim1[i]=2 \times t_i-p_i,lim2[i]=2 \times t_i+p_i\)
对于一个 \(i\) 找到一个可以转移的 \(j\) 就要满足 \(lim1[i]\geq lim1[j]\&\&lim2[i]\geq lim2[j]\)
然后就转化为了经典二维数点问题，先离散化一下，再通过排序解决一层限制，树状数组解决第二层问题
代码：
点击查看代码
#include<bits/stdc++.h>
#define pii pair<int,int>
using namespace std;
const int N=1e5+5;
int w,n;
int tr[N],dp[N];
struct freepie{
int t,p,v,lim1,lim2;
}pie[N];
pii lim1[N],lim2[N];
int lowbit(int x){
return x&(-x);
}
void add(int x,int z){
for(;x<=n;x+=lowbit(x)){
tr[x]=max(z,tr[x]);
}
}
int query(int x){
int res=0;
for(;x;x-=lowbit(x)){
res=max(res,tr[x]);
}
return res;
}
bool cmp(freepie x,freepie y){
return x.lim1<y.lim1;
}
int main(){
scanf("%d%d",&w,&n);
for(int i=1;i<=n;i++){
int t,p,v;
scanf("%d%d%d",&t,&p,&v);
pie[i]={t,p,v};
}
for(int i=1;i<=n;i++){
lim1[i]={2*pie[i].t-pie[i].p,i};
lim2[i]={pie[i].p+2*pie[i].t,i};
}
sort(lim1+1,lim1+n+1);
sort(lim2+1,lim2+n+1);
for(int i=1;i<=n;i++){
pie[lim1[i].second].lim1=i;
pie[lim2[i].second].lim2=i;
}
sort(pie+1,pie+n+1,cmp);
for(int i=1;i<=n;i++){
int mx=query(pie[i].lim2);
dp[i]=mx+pie[i].v;
add(pie[i].lim2,dp[i]);
}
printf("%d",query(n));
}
线段树优化dp
基站选址
戳我查看题解
很恶心的一道题
首先我们设 \(dp[i][j]\) 表示在第 \(i\) 个村庄设基站，前面设立了 \(j\) 个基站所承受的最小代价设 \(pay(i,j)\) 表示在第 \(i-1,j+1\) 设立基站，中间不设立基站所需要赔偿的费用
转移方程：
\[dp[i][j]=\min \\\{ dp[k][j-1]+pay(k+1,i-1)\\\}-c[i]
\]
首先因为 \(dp[i][j]\) 只与 \(dp[i][j-1]\) 有关，所以可以压掉一维
\[dp[i]=\min \\\{ dp[k]+pay(k+1,i-1)\\\}-c[i]
\]
难点来了，我们发现状态数没法继续优化了，复杂度瓶颈卡在求 \(\min \\\{ dp[k]+pay(k+1,i-1)\\\}\) 上，显然这一维我们是要用数据结构来维护，但是处理出 \(pay(i,j)\) 是麻烦的
我们考虑对于一个 \(g\) 何时会给它赔偿？
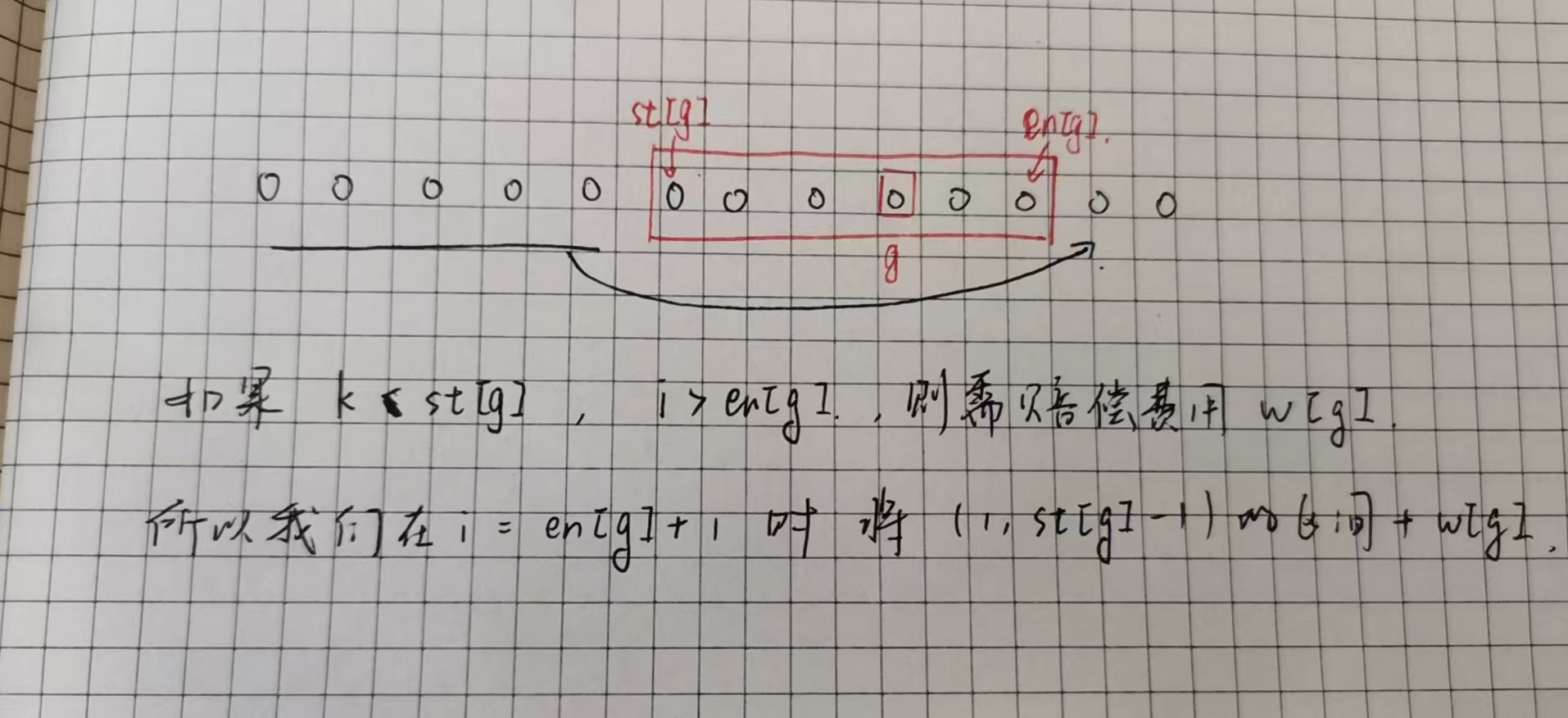
所以用线段树维护区间最小值和区间加即可
细节：
- 在 \(i\) 处，用 \(vector\) 存一下 \(i=en[g]\)的 \(g\)
- 最后设一个虚点 \(n+1\)，\(d[n+1]\) 设为 \(inf\)，用来统计答案，注意 \(k\) 要加1
- 当设立第一个基站时不遵循转移规律，要手动统计答案
- 在 \(i=1\) 时没有基站可以转移，要手动转移
- 当 \(st[g]=1\) 时，若不特判会 \(RE\)
- \(st[g],en[g]\) 可以通过二分来预处理出来
- 每一轮转移记得清空懒标记数组
- 在转移之前就把上一轮的 \(dp\) 状态放进线段树里会更方便一些
代码：
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e4+20,inf=1e18;
int n,k,ans=inf;
int d[N],c[N],s[N],w[N],tr[4*N],st[N],en[N],dp[N],add[4*N];
vector<int>del[N];
int queryst(int i){
int l=1,r=i;
while(l<r){
int mid=(l+r)>>1;
if(d[mid]<d[i]-s[i]) l=mid+1;
else r=mid;
}
return l;
}
int queryen(int i){
int l=i,r=n;
while(l<r){
int mid=(l+r+1)>>1;
if(d[mid]>d[i]+s[i]) r=mid-1;
else l=mid;
}
return l;
}
void build(int k,int l,int r){
tr[k]=add[k]=0;
if(l==r){
tr[k]=dp[l];
return;
}
int mid=(l+r)>>1;
build(k*2,l,mid);
build(k*2+1,mid+1,r);
tr[k]=min(tr[k*2],tr[k*2+1]);
}
void Add(int k,int l,int r,int z){
add[k]+=z;
tr[k]+=z;
}
void pushdown(int k,int l,int r){
int mid=(l+r)>>1;
Add(k*2,l,mid,add[k]);
Add(k*2+1,mid+1,r,add[k]);
add[k]=0;
}
int query(int k,int l,int r,int x,int y){
if(x<=l&&r<=y){
return tr[k];
}
pushdown(k,l,r);
int mid=(l+r)>>1,res=inf;
if(x<=mid) res=min(res,query(k*2,l,mid,x,y));
if(y>mid) res=min(res,query(k*2+1,mid+1,r,x,y));
return res;
}
void longchange(int k,int l,int r,int x,int y,int z){
if(x<=l&&r<=y){
tr[k]+=z;
add[k]+=z;
return;
}
pushdown(k,l,r);
int mid=(l+r)>>1;
if(x<=mid) longchange(k*2,l,mid,x,y,z);
if(y>mid) longchange(k*2+1,mid+1,r,x,y,z);
tr[k]=min(tr[k*2],tr[k*2+1]);
}
signed main(){
scanf("%lld%lld",&n,&k);
for(int i=2;i<=n;i++){
scanf("%lld",&d[i]);
}
for(int i=1;i<=n;i++){
scanf("%lld",&c[i]);
}
for(int i=1;i<=n;i++){
scanf("%lld",&s[i]);
}
for(int i=1;i<=n;i++){
scanf("%lld",&w[i]);
}
k++,n++;
d[n]=inf;
for(int i=1;i<=n;i++){
st[i]=queryst(i);
en[i]=queryen(i);
del[en[i]].push_back(i);
}
memset(tr,0x3f3f3f3f,sizeof(tr));
int gg=0;
for(int j=1;j<=k;j++){
build(1,1,n);
for(int i=1;i<=n;i++){
int mn=0;
if(i!=1) mn=query(1,1,n,1,i-1);
if(j==1) mn=gg;
dp[i]=mn+c[i];
if(i==n&&j!=1) ans=min(dp[i],ans);
for(int g:del[i]){
if(j==1) gg+=w[g];
if(st[g]==1) continue;
longchange(1,1,n,1,st[g]-1,w[g]);
}
}
}
printf("%lld",ans);
}
Mowing the Lawn G
戳我查看题解
一道单调队列优化dp的题
我们考虑暴力怎么做？
设 \(dp[i]\) 为选了 \(i\) 所能获得的最大劳动力，\(num(j,i)\) 表示 \(j\) 到 \(i\) 的劳动力
转移方程：
\[dp[i]=\max^{i-1}_{j=i-k+1}\\\{ dp[j-2]+num(j,i)\\\}
\]
然后考虑如何加速转移，会发现从 \(i\) 转移到 \(i+1\) 时，所有状态都会加上 \(e[i+1]\) 的贡献
所以我们就用线段树维护一下区间修改和最大值就可以了！
细节：我们这样转移有点问题，就是有一种可能是存在一种不选 \(i\) 却更优的方案
例：
7 2
20 20 1 1 20 20 1
于是就再维护一个前缀状态的最大值，比较更新一下 \(dp[i]\) 即可
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=4e5+20;
int n,k,ans;
int e[N],tr[N],add[N],dp[N];
void Add(int k,int l,int r,int z){
tr[k]+=z;
add[k]+=z;
}
void pushdown(int k,int l,int r){
int mid=(l+r)>>1;
Add(k*2,l,mid,add[k]);
Add(k*2+1,mid+1,r,add[k]);
add[k]=0;
}
void change(int k,int l,int r,int x,int z){
if(l==r&&l==x){
tr[k]=z;
return;
}
int mid=(l+r)>>1;
if(x<=mid) change(k*2,l,mid,x,z);
else change(k*2+1,mid+1,r,x,z);
tr[k]=max(tr[k*2],tr[k*2+1]);
}
int query(int k,int l,int r,int x,int y){
if(x<=l&&r<=y){
return tr[k];
}
pushdown(k,l,r);
int mid=(l+r)>>1,res=0;
if(x<=mid) res=max(res,query(k*2,l,mid,x,y));
if(y>mid) res=max(res,query(k*2+1,mid+1,r,x,y));
return res;
}
void longchange(int k,int l,int r,int x,int y,int z){
if(x<=l&&r<=y){
Add(k,l,r,z);
return;
}
pushdown(k,l,r);
int mid=(l+r)>>1;
if(x<=mid) longchange(k*2,l,mid,x,y,z);
if(y>mid) longchange(k*2+1,mid+1,r,x,y,z);
tr[k]=max(tr[k*2],tr[k*2+1]);
}
signed main(){
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n;i++){
scanf("%lld",&e[i]);
}
for(int i=1;i<=n;i++){
if(i!=1) change(1,1,n,i,dp[i-2]);
longchange(1,1,n,max(1ll,i-k+1),i,e[i]);
dp[i]=max(ans,query(1,1,n,max(1ll,i-k+1),i));
ans=max(ans,dp[i]);
// printf("%d ",dp[i]);
}
// printf("\n");
printf("%lld",ans);
}
单调队列优化dp
PTA-Little Bird
戳我查看题解
首先设 \(dp[i]\) 表示跳到第 \(i\) 棵树能获得的最小劳累值
转移式子：
\[dp[i]=min^{i-1}_{j=i-k}\\\{dp[j]+[d_i \geq d_j]\\\}
\]
然后考虑这样一件事情，\([d_i \geq d_j]\) 顶多带来 1 的贡献，所以我们可以维护 \(dp[j]\) 的最小值（且要保证 \(d_j\) 尽量大），这样答案就变成了
\[dp[i]=min^{i-1}_{j=i-k}\\\{dp[j]\\\}+[d_i \geq d_j]
\]
用单调队列比较（在 \(dp[j]\) 最小的情况下要求 \(d_j\) 最大）维护即可
代码：
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,q,k,l,r;
int d[N],dq[N],dp[N];
int query(int k){
l=1,r=1;
dq[1]=1;
for(int i=2;i<=n;i++){
if(dq[l]<i-k) l++;
dp[i]=dp[dq[l]]+(d[dq[l]]<=d[i]);
while(l<=r&&(dp[dq[r]]>dp[i]||(dp[dq[r]]==dp[i]&&d[dq[r]]<=d[i]))) r--;
dq[++r]=i;
}
return dp[n];
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&d[i]);
}
scanf("%d",&q);
for(int i=1;i<=q;i++){
scanf("%d",&k);
printf("%d\n",query(k));
}
}
宝物筛选
戳我查看题解
单调队列优化多重背包，典中典
首先我们有压掉一维的转移方程
\[dp[j]=\max^{m_i}_{k=0}\\\{ dp[j-k*w_i]+v_i*k\\\}
\]
然后考虑状态之间有重叠，于是进行优化
设 \(j=k_1*w+d\)，于是有
\[dp[k_1*w+d]=\max^{m_i}_{k=0}\\\{ dp[(k_1-k)*w+d]+(k_1-k)*v\\\}+k_1*v
\]
于是我们枚举余数 \(d\)，然后用单调队列维护一下 \(\max^{m_i}_{k=0}\\\{ dp[(k_1-k)*w+d]+(k_1-k)*v\\\}\)，正常转移即可
细节：不要让 \(k_1*w+d>W\)，然后如果倒叙枚举不明白，滚动数组是最好的选择
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=105,M=4e4+5;
int n,W,l,r,ans;
int v[N],w[N],m[N],dp[2][M],num[M],q[M];
signed main(){
scanf("%lld%lld",&n,&W);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&v[i],&w[i],&m[i]);
}
int now=0,old=1;
for(int i=1;i<=n;i++){
swap(now,old);
for(int d=0;d<w[i];d++){
l=1,r=0;
for(int k=0;k<=W/w[i];k++){
if(k*w[i]+d>W) continue;
num[k]=dp[old][k*w[i]+d]-k*v[i];
if(q[l]<k-m[i]) l++;
while(l<=r&&num[q[r]]<=num[k]) r--;
q[++r]=k;
int g=num[q[l]];
if(l>r) g=0;
dp[now][k*w[i]+d]=g+k*v[i];
ans=max(ans,dp[now][k*w[i]+d]);
}
}
}
printf("%lld",ans);
}
股票交易
戳我查看题解
状态设计及转移方程很好推
对于 3，4 状转方程维护两个单调队列即可解决
代码：
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2005,inf=1e9;
int T,M,W,l1,l2,r1,r2,ans;
int ap[N],bp[N],as[N],bs[N],dp[N][N],num1[N][N],num2[N][N],q1[N],q2[N];
void add1(int i,int k){
int g=i-W-1;
if(g<1) return;
if(k>M) return;
while(l1<=r1&&num1[g][q1[r1]]<=num1[g][k]) r1--;
q1[++r1]=k;
}
void add2(int i,int k){
int g=i-W-1;
if(g<1) return;
if(k<0) return;
while(l2<=r2&&num2[g][q2[r2]]<=num2[g][k]) r2--;
q2[++r2]=k;
}
int query1(int i,int j){
int g=i-W-1;
if(g<1) return -inf;
if(q1[l1]<j) l1++;
return num1[g][q1[l1]];
}
int query2(int i,int j){
int g=i-W-1;
if(g<1) return -inf;
if(q2[l2]<j-as[i]) l2++;
return num2[g][q2[l2]];
}
int main(){
scanf("%d%d%d",&T,&M,&W);
for(int i=1;i<=T;i++){
scanf("%d%d%d%d",&ap[i],&bp[i],&as[i],&bs[i]);
}
for(int i=0;i<=T;i++){
for(int j=0;j<=M;j++){
dp[i][j]=-inf;
}
}
for(int i=1;i<=T;i++){
l1=l2=1,r1=r2=0;
int g=i-W-1;
if(g>0){
for(int k=0;k<=M;k++){
num1[g][k]=dp[g][k]+bp[i]*k;
num2[g][k]=dp[g][k]+ap[i]*k;
}
}
for(int k=0;k<=bs[i];k++) add1(i,k);
for(int j=0;j<=M;j++){
dp[i][j]=dp[i-1][j];
if(j<=as[i]) dp[i][j]=max(-ap[i]*j,dp[i][j]);
add1(i,j+bs[i]);
add2(i,j);
dp[i][j]=max(dp[i][j],query1(i,j)-bp[i]*j);
dp[i][j]=max(dp[i][j],query2(i,j)-ap[i]*j);
ans=max(ans,dp[i][j]);
}
}
printf("%d",ans);
}
瑰丽华尔兹
戳我查看题解
简单题，切了
首先现设 \(dp[i][j][k]\) 表示在 \((i,j)\) ，第 \(k\) 段区间末尾最少使用的魔法次数
因为第三个维度 \(k\) 转移时只与 \(k-1\) 有关，所以用滚动数组压掉一维
然后转移方程需要类讨论，这里举例 \(d=1\) 时，设 \(len=t_i-s_i+1\)：
\[dp[i][j]=\min_{k=i}^{i+len}\\\{dp[k][j]+len-(k-i)\\\}
\]
我们用单调队列维护，所以去掉不属于 \(k\) 的 \(j\)：
\[dp[i][j]=\min_{k=i}^{i+len}\\\{dp[k][j]-k\\\}+len+i
\]
然后从大到小枚举 \(j\)，用单调队列转移即可
\(d=2,3,4\) 时同理，不做赘述
代码：
(代码中有几行调试，为每段的dp值，如果调不出来可以参考比较一下)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=205,inf=1e9;
int n,m,sx,sy,K,now,old,l,r,ans;
int s[N],t[N],d[N],dp[2][N][N],lim[N][N],q[N];
char c[N];
void query1(int len){
for(int j=1;j<=m;j++){
l=1,r=0;
for(int i=n;i>=1;i--){
if(lim[i][j]){
l=1,r=0;
continue;
}
if(l<=r&&q[l]>i+len) l++;
while(l<=r&&dp[old][q[r]][j]-q[r]>=dp[old][i][j]-i) r--;
q[++r]=i;
dp[now][i][j]=dp[old][q[l]][j]+len-q[l]+i;
}
}
}
void query2(int len){
for(int j=1;j<=m;j++){
l=1,r=0;
for(int i=1;i<=n;i++){
if(lim[i][j]){
l=1,r=0;
continue;
}
if(l<=r&&q[l]<i-len) l++;
while(l<=r&&dp[old][q[r]][j]+q[r]>=dp[old][i][j]+i) r--;
q[++r]=i;
dp[now][i][j]=dp[old][q[l]][j]+q[l]-i+len;
}
}
}
void query3(int len){
for(int i=1;i<=n;i++){
l=1,r=0;
for(int j=m;j>=1;j--){
if(lim[i][j]){
l=1,r=0;
continue;
}
if(l<=r&&q[l]>j+len) l++;
while(l<=r&&dp[old][i][q[r]]-q[r]>=dp[old][i][j]-j) r--;
q[++r]=j;
dp[now][i][j]=dp[old][i][q[l]]-q[l]+len+j;
}
}
}
void query4(int len){
for(int i=1;i<=n;i++){
l=1,r=0;
for(int j=1;j<=m;j++){
if(lim[i][j]){
l=1,r=0;
continue;
}
if(l<=r&&q[l]<j-len) l++;
while(l<=r&&dp[old][i][q[r]]+q[r]>=dp[old][i][j]+j) r--;
q[++r]=j;
dp[now][i][j]=dp[old][i][q[l]]+q[l]-j+len;
}
}
}
int main(){
scanf("%d%d%d%d%d",&n,&m,&sx,&sy,&K);
for(int i=1;i<=n;i++){
scanf("%s",c+1);
for(int j=1;j<=m;j++){
if(c[j]=='x') lim[i][j]=1;
else lim[i][j]=0;
}
}
for(int i=1;i<=K;i++){
scanf("%d%d%d",&s[i],&t[i],&d[i]);
}
now=0,old=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dp[now][i][j]=dp[old][i][j]=inf;
}
}
dp[now][sx][sy]=0;
for(int i=1;i<=K;i++){
swap(old,now);
int len=t[i]-s[i]+1;
if(d[i]==1) query1(len);
if(d[i]==2) query2(len);
if(d[i]==3) query3(len);
if(d[i]==4) query4(len);
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m;j++){
// printf("%d ",dp[now][i][j]);
// }
// printf("\n");
// }
}
ans=inf;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
ans=min(ans,dp[now][i][j]);
}
}
printf("%d",t[K]-ans);
}
