CF1945题解

CF1945A

贪心简单题
先把b自己内部组合，再考虑与c组合

CF1945B

简单题数学题

因为在0_{m的时间内一定能覆盖所有的情况，所以对0}m的时间内最多烟花数进行小学2年纪计算即可

CF1945C

简单题

枚举每一个断点，记录答案即可

CF1945D

挺好玩的一道贪心题。

转化一下式子，我们发现 \(a[i],b[i]\) 的选择过程类似于一个上下反复横跳的最终的选取停止在 \(a\) 数组的一个过程，如下图。

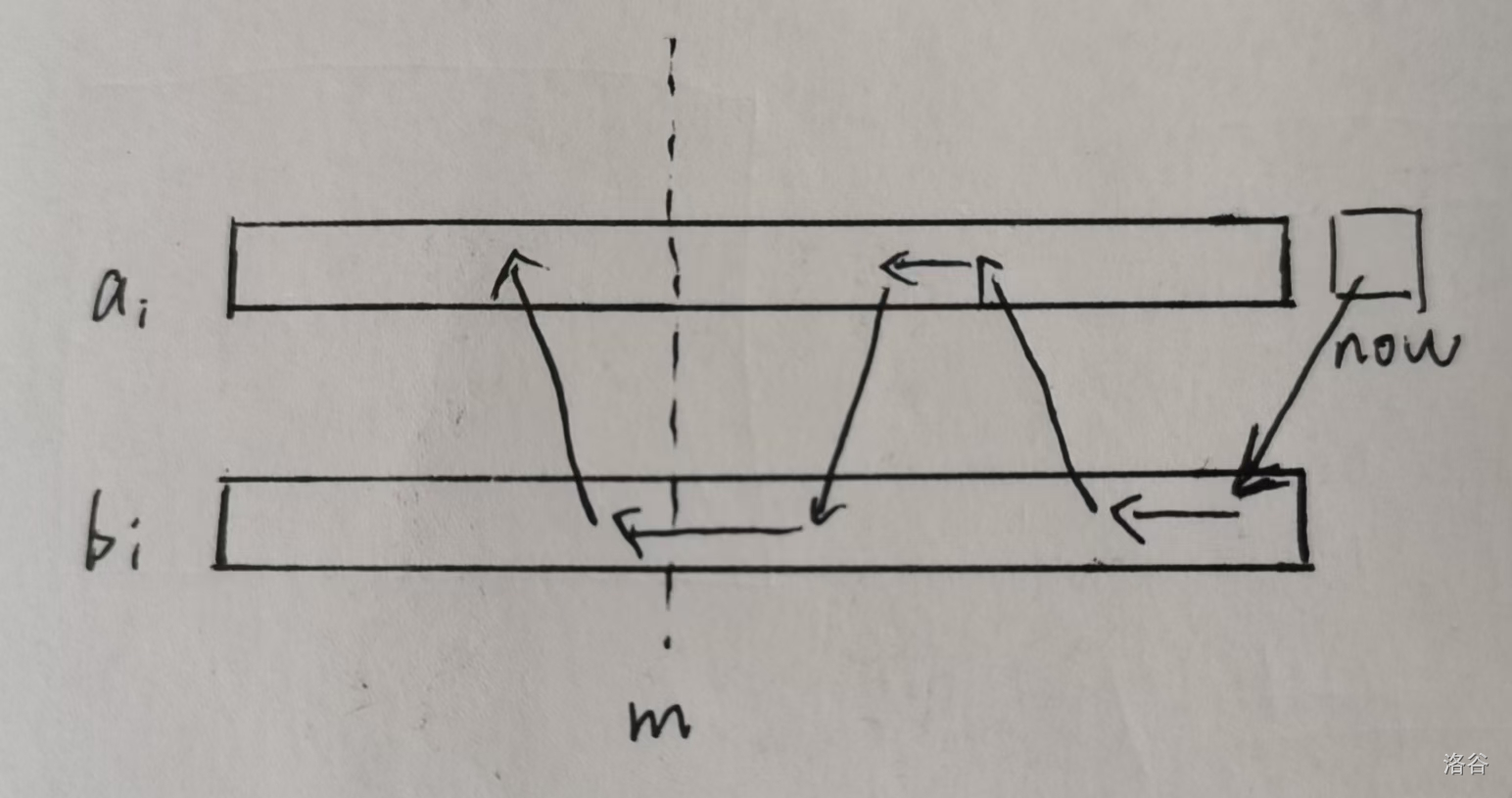
注意到对于一个 \(j\) 位置，我们只会在 \(a[j]\)，\(b[j]\) 中选一个对答案产生贡献，且在 \(m+1,m+2,\cdots, n\) 之间选哪一个数并不会对之后的决策产生影响（无后效性）。

因为在 \(m+1,m+2,\cdots, n\) 之间我们每个选择是独立的，所以在 \(m+1,m+2,\cdots, n\) 之间直接贪心，对答案的贡献即为 \(\sum_{i=m+1}^n \min\{a[i],b[i]\}\)。

那么在 \(1,2,\cdots,m\) 这一段对答案的贡献就显而易见了，因为在这一段中只要选择了 \(a[j]\) 就停止选择了，所以答案的组成既是一段 \(b_{j+1},b_{j+2} ,\cdots ,b_m\) 再加上 \(a_j\)。

所以只需要统计一下 \(\min_{i=1}^m\{\sum_{j=i+1}^mb[j]+a[i]\}\) 即可

最终答案即是这两段贡献的加和

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5,inf=1e18+5;
int n,m,t;
int a[N],b[N];
signed main(){
	scanf("%lld",&t);
	while(t--){
		scanf("%lld%lld",&n,&m);
		for(int i=1;i<=n;i++){
			scanf("%lld",&a[i]);
		}
		for(int i=1;i<=n;i++){
			scanf("%lld",&b[i]);
		}
		int cnt=0,ans=inf;
		for(int i=n;i>=1;i--){
			if(i>m){
				if(a[i]>b[i]){
					cnt+=b[i];
				}
				else{
					cnt+=a[i];
				}
			}
			else{
				ans=min(ans,cnt+a[i]);
				cnt+=b[i];
			}
		}
		printf("%lld\n",ans);
	}
}

CF1945E

非常好玩的一道题，使我的脑子旋转

首先我先从x有序和二进制这两方面考虑，然后发现这是大大的没前途的

于是我有前途的打开了题解

首先我们考虑先进行一遍二分得出的答案为 \(a[l]\)，然后考虑一条性质如果我们在二分的时候没有访问到x这个元素，那么我们直接将 \(l,x\) 交换是合法的

所以我们由这条性质进行一个分讨：

若二分时没有访问到这个元素直接一步交换

若访问到了则在进行一个分讨：

若 \(p[l]<x\) 则考虑将 \(l,x\) 交换，二分时在x这一位上因为 \(m<=x\) 所以 \(l=m\)，而交换后因为 \(p[l]<x\) 所以 \(l\) 依旧等于 \(m\)，所以对于这种情况，还是交换\(l,x\)

若 \(p[l]>x\) 我们考虑只要 \(a[m]<=x\) 时 \(l\) 就会等于 \(m\) 所以说，因为 \(a[m]<=x\) ，所以 \(l\) 必然是没有被更新过的，所以二分过程中也没有访问到x，所以直接交换就完了

综上所述，我们就跑一遍二分然后交换 \(a[l],x\) 即可，注意特判 \(a[l]==x\)直接输出0即可