CF1187题解
前言
这套题相对来讲难度不算高，并且质量也很好，建议尝试
CF1187A
一眼秒，但我没有
考虑s，t只有这一种排列方式，所以取一下 \(max(n-s,n-t)\)
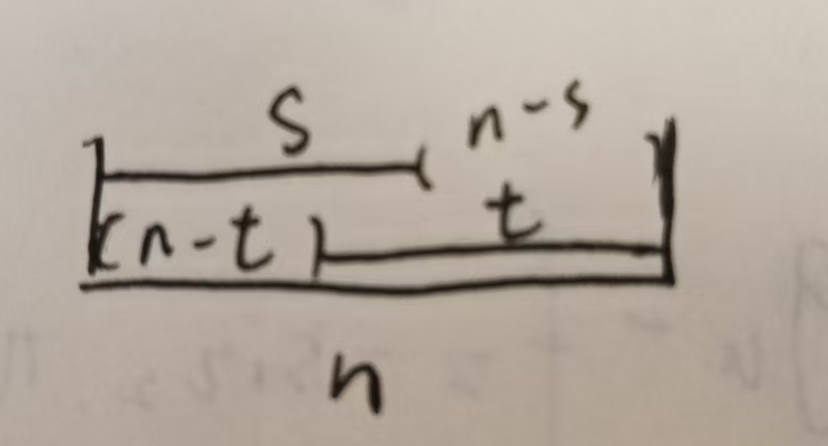
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int T,n,s,t;
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d%d",&n,&s,&t);
printf("%d\n",n-min(s,t)+1);
}
}
CF1187B
一眼秒，先预处理出每一个字母出现的次数所对应的下标
然后对于每个串O（1）查询即可
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int ans,n,m;
int num[30][N],lst[30],tot[30];
char s[N],c[N];
int main(){
scanf("%d",&n);
scanf("%s",s+1);
for(int i=1;i<=n;i++){
num[s[i]-'a'][++lst[s[i]-'a']]=i;
}
scanf("%d",&m);
for(int i=1;i<=m;i++){
scanf("%s",c+1);
int len=strlen(c+1);
for(int j=1;j<=len;j++){
tot[c[j]-'a']++;
}
for(int j=0;j<=25;j++){
ans=max(num[j][tot[j]],ans);
tot[j]=0;
}
printf("%d\n",ans);
ans=0;
}
}
题目链接CF1187C
考虑 \(t=0\) 时当且仅当区间内存在一个严格降序，这显然是不好处理的
\(t=1\) 时区间内所有的数都要满足不降序列，这显然是很好处理的
我们先设 \(z[i]=1\) 为 \(a[i]<=a[i+1]\)，为 \(z[i]=0\) 则有 \(a[i]<=a[i+1]\) ， \(z[i]=2\) 则不确定
然后我们先处理 \(t=1\) 的情况，因为 \(t=0\) 时无法立即处理
将所有的 \(t=1\) 的区间暴力修改为 \(z[i]=1\) ，然后再暴力判断 \(t=0\) 区间内是否存在 \(z[i]!=1\)的情况，若没有则不合法，否则修改为 \(z[i]=0\)
在处理完 \(z\) 数组后，我们按照 \(z\) 的大小关系构造一种可行方案即可
注意：因为 \(z\) 数组的定义 \(z[i]=1\) 为 \(a[i]<=a[i+1]\) ，所以区间要从 \(l\) 枚举到 \(r-1\)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m,op,l,r,cnt;
int z[N],el[N],er[N];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) z[i]=2;
for(int i=1;i<=m;i++){
scanf("%d%d%d",&op,&l,&r);
if(op==1){
for(int j=l;j<r;j++){
z[j]=1;
}
}
else{
cnt++;
el[cnt]=l,er[cnt]=r;
}
}
for(int i=1;i<=cnt;i++){
bool tot=1;
for(int j=el[i];j<er[i];j++){
if(z[j]!=1){
z[j]=0;
tot=0;
break;
}
}
if(tot){
printf("NO\n");
return 0;
}
}
printf("YES\n");
int num=1000;
for(int i=1;i<=n;i++){
printf("%d ",num);
if(z[i]) num++;
else num--;
}
}
CF1187D
这篇洛谷题解是我写的，这里是网址
额能帮我点一个赞吗QWQ
请先食用我的题解在阅读以下文字
针对我的题解有些没有展开的内容，我进行一下补充
如果还没明白，可以线下q我
CF1187E
前置知识，换根dp
没有学过的可以像我一样恶补一下
换根dp是用来解决要求以各个点为根时答案的问题的
换根dp本质上就是进行两次dp，第一次随便选一个点作为根，统计一下以这个点为根的答案，然后在考虑将一个棵树的根转到它的子节点对答案产生的影响来统计答案
考虑此题
我们只需要选择一个点开始，剩下的答案就是确定的
当我们从1开始时，显然 \(ans[1]=siz[1]+所有儿子的f[i]\)，f[i]为在i为父亲节点的子树內所有点的子树大小的加和，也就是说 \(f[u]=\sum f[v]+siz[u]\)
然后考虑从父亲u转移到儿子v时对ans的影响
这里我们用从1转移到2来举例
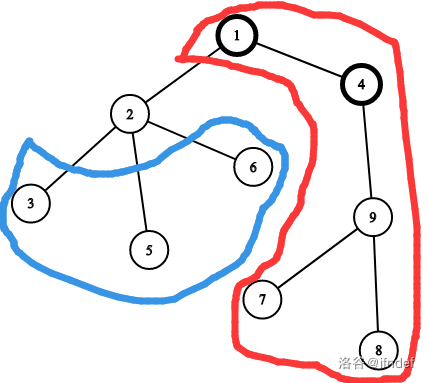
先考虑子树内（蓝色圈内）的的点对答案的影响,就是\(f[v]-siz[v]\)
在考虑红色圈内的影响为 \(ans[u]-f[v]-siz[v]\)
其中 \(ans[u]=siz[u]+\sum f[v]\)
考虑删去了f[v]答案，siz[u]也该减一个siz[v]，所以答案就是这个
最后我们把答案合起来 \(ans[v]=ans[u]-2*siz[v]\) 进行树形dp即可
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n,u,v,tot;
int ans[N],siz[N],vis[N],f[N];
vector<int>b[N];
void dfs1(int x){
for(auto i:b[x]){
if(vis[i]) continue;
vis[i]=1;
dfs1(i);
siz[x]+=siz[i];
f[x]+=f[i];
}
f[x]+=siz[x];
}
void dfs2(int x){
for(auto i:b[x]){
if(vis[i]) continue;
vis[i]=1;
ans[i]=ans[x]-siz[i]*2+n;
dfs2(i);
}
}
signed main(){
scanf("%lld",&n);
for(int i=1;i<n;i++){
scanf("%lld%lld",&u,&v);
b[u].push_back(v);
b[v].push_back(u);
}
for(int i=1;i<=n;i++) siz[i]=1;
vis[1]=1;
dfs1(1);
ans[1]=f[1];
for(int i=1;i<=n;i++) vis[i]=0;
vis[1]=1;
dfs2(1);
for(int i=1;i<=n;i++){
tot=max(tot,ans[i]);
}
printf("%lld",tot);
}
