有关线段树的一些细节理解+ybt题目练习

写在前面

本菜鸡线段树学了好多遍
但是每次写还是得很长时间
有时有一个细节还要琢磨半天
所以为了今后避免以上事情发生
本菜鸡决定将这么长时间以来对线段树的认识汇总
好日后清算

ps:写道一半又卡住了,感谢nyn大佬指点迷津

ps\(^2\)：正好做到ybt线段树这一章，就扒出我原来的题解继续写吧

模板

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5;
int add[N*4],tr[N*4],a[N];//为什么开4倍,见下文
int n,y,x,op,m,k;
void build(int k,int l,int r){
	if(l==r){
		tr[k]=a[l];
		return;
	}  
	int mid=(l+r)/2;
	build(2*k,l,mid);
	build(2*k+1,mid+1,r);
	tr[k]=tr[2*k]+tr[2*k+1];
}
void Add(int k,int l,int r,int v){
	tr[k]+=v*(r-l+1);
	add[k]+=v;//标记代表的是下一位需要修改的值,本位值已经正确
}
void pushdown(int k,int l,int r){
	if(!add[k]) return;//可写可不写
	int mid=(l+r)/2;
	Add(2*k,l,mid,add[k]);
	Add(2*k+1,mid+1,r,add[k]);
	add[k]=0;//标记下传到下一位,下一位值已经正确
}
void longchange(int k,int l,int r,int x,int y,int v){
	if(x<=l&&r<=y){
		add[k]+=v;//将标记修改为新修改
		tr[k]+=v*(r-l+1);//将本位改为正确
		return;//需要return不然会一直循环下去
	}
	pushdown(k,l,r);//将旧标记下传,注意这个标记是旧的标记,新的标记还未添加
	int mid=(l+r)/2;
	if(x<=mid) longchange(2*k,l,mid,x,y,v);
	if(y>mid) longchange(2*k+1,mid+1,r,x,y,v);
	tr[k]=tr[2*k]+tr[2*k+1];//它的下一位经过新标记修改后已经正确,它还是错误的,所以重新由正确的转移过来
}
int longquery(int k,int l,int r,int x,int y){
	if(x<=l&&r<=y){//因为不一定要查询的区间正好卡在线段树维护的整体上,反正只要这个区间在查询的区间内就对答案有贡献
		return tr[k];//因为这个位置已经在上一位下传标记时修改完毕,所以不需要新的修改
	}
	pushdown(k,l,r);//同理下传原来的标记,但因为是区间查询所以不存在新旧标记问题
	int res=0,mid=(l+r)/2;
	if(x<=mid) res+=longquery(2*k,l,mid,x,y);
	if(y>mid) res+=longquery(2*k+1,mid+1,r,x,y);//为什么不是>=?  因为y>=mid+1,就是y>mid
	return res;
}
signed main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
	}
	build(1,1,n);//原来的l,r都是从1~n开始搜的
	for(int i=1;i<=m;i++){
		scanf("%lld%lld%lld",&op,&x,&y);
		if(op==1){
			scanf("%lld",&k);
			longchange(1,1,n,x,y,k);
		}
		if(op==2){
			printf("%lld\n",longquery(1,1,n,x,y)); 
		}
	}
}

至于为什么线段树要开4倍区间:

且看我证明
一颗完全二叉树,每一层的节点数为 \(2^d\) ,\(d\) 代表这一层的深度
所以对于一颗完全二叉树,总结点个数为 \(2^0+2^1+2^2+\cdots+2^n=2^{n+1}-1\)
如何证明呢?
考虑两种证法
1.二进制拆分将 \(2^0,2^1,2^2,\cdots,2^n,2^{n+1}-1\)逐个拆分,会得到 \(1,10,100,1000,\cdots,11111\ldots\),不多赘述
2.(还是感谢nyn大佬)将等式两边同 \(+1\),即可
考虑对于一颗有 \(n\) 个叶子节点的完全二叉树的深度为 \(\log_2^n\)
节点个数为\(2^{\log_2^n+1}-1=2n-1\)
而线段树并不是完全二叉树

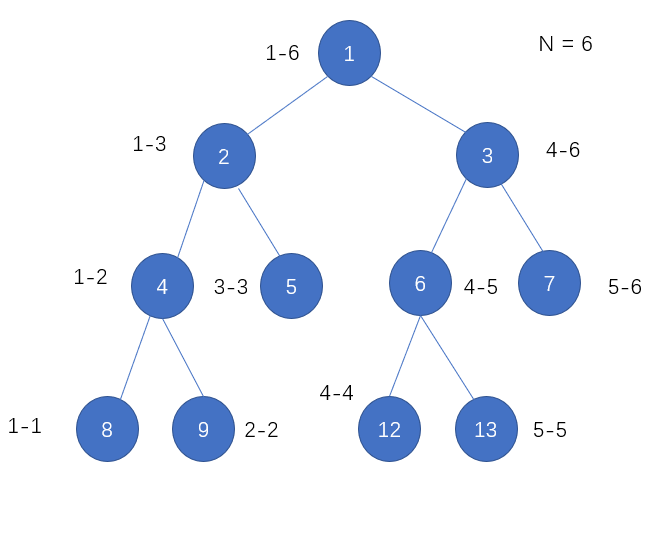
所以有可能会多出一层
所以，对于n个点，比n大的最小二次幂即为线段树最底层的结点数，所以所有结点数为 \(2^{\lceil{\log_2^n}\rceil+1}-1<=4n-1\)
最大即为 \(4n\)

ybt例题

T1，2

板子题

T3

之前一直畏惧的一道题，觉得写起来很难，但是真正写完之后感觉还好

代码

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e6+5;
int n,m;
int a[N];
struct dot{
	int left,right,tot,sum;
}tr[N];
dot merge(dot x,dot y){
	dot c;
	c.sum=x.sum+y.sum;
	c.tot=max(x.right+y.left,max(x.tot,y.tot));
	c.left=max(x.left,x.sum+y.left);
	c.right=max(y.right,x.right+y.sum);
	return c;
}
void build(int k,int l,int r){
	if(l==r){
		tr[k]={a[l],a[l],a[l],a[l]};
		return;
	}
	int mid=(l+r)>>1;
	build(2*k,l,mid);
	build(2*k+1,mid+1,r);
	tr[k]=merge(tr[2*k],tr[2*k+1]);
}
void change(int k,int l,int r,int x,int v){
	if(l==r&&l==x){
		tr[k]={v,v,v,v};
		return;
	}
	int mid=(l+r)>>1;
	if(x<=mid)  change(k*2,l,mid,x,v);
	else  change(k*2+1,mid+1,r,x,v);
	tr[k]=merge(tr[k*2],tr[k*2+1]);
}
dot query(int k,int l,int r,int x,int y){
	if(x<=l&&r<=y){
		return tr[k];
	}
	int mid=(l+r)>>1;
	if(y<=mid)  return query(k*2,l,mid,x,y);
	else if(mid<x)  return query(k*2+1,mid+1,r,x,y);
	else  return merge(query(k*2,l,mid,x,y),query(k*2+1,mid+1,r,x,y));
}
signed main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
	}
	build(1,1,n);
	for(int i=1;i<=m;i++){
		int op,x,y;
		scanf("%lld%lld%lld",&op,&x,&y);
		if(op==1){
			if(x>y)  swap(x,y);
			int ans=query(1,1,n,x,y).tot;
			printf("%lld\n",ans);
		}
		else{
			change(1,1,n,x,y);
		}
	}
}

T4

首先又有区间乘又有区间加，那么我们考虑应该怎么办呢？

只需要对 Add 操作稍作修改即可

T5：

不知为何，这题我直接就做出来了，虽然调了很久，发现query没加pushdown

我们发现此题有很好的性质，就是只有26个英文字母，也就是说排序的数字只有1~26，我们对每一个字符开一个线段树，记录它的位置

对于一次排序操作，升序排序即升序枚举每一个字母，统计其区间个数 \(k\)，然后将其区间内的各个位置上先赋值为0，再将没用过的前 \(k\) 个位置上都赋值为1即可

最后查询一下在第i个位置上哪个线段树上有字母即可

T6：

板子题，只需要知道一个结论就是dfs序在一个子树內连续，就可以区间操作即可

T7：

想破脑袋没想明白竟然取模运算直接暴力修改即可

我们首先进行一个证明：一个数有效取模 \(log\) 次就会变为1

2种理解方法：

1.从除法运算入手：

考虑取模运算 \(x%y\) 相当于 \(x/y\) 余上 \(k\) 因为 \(k<y\) 然而考虑一个数转化为二进制后除以一个数，起码会减少一个二进制位，最多减少 \(log\) 次，证毕

2.从式子本身入手：

在有效取模时
\(x\mod y=k\ \ ->x=ny+k\) 考虑 \(y>k,n>=1\) 所以 \(k\)最大是x的一半，所以取模运算最多进行 \(log\) 次

考虑本题，一共有n个数，最多有m次修改，就是总共有 \(nlogn+mlogn\) 的贡献，考虑每次取模运算最低是将n个数中的一个数修改为其的一半，也就是带来-1的贡献，那么也就是说如果有效取模的话最多进行 \(nlogn+mlogn\) 次，因是在线段树树上操作，所以自身还会带一个 \(logn\) 总复杂度 \(nlog^2n\) 可以通过本题

如何保证对每一个数有效取模，考虑我们只有对比模数大的数取模才算有效取模，所以我们统计一个区间最大值，如果该区间内有比模数大的数就说明该区间内有数需要有效取模，反之直接退出即可

T8：

一眼秒了

考虑传输魔法的过程相当于是 \((l,r),(l+1,r),(l+2,r)\dots (r,r)\) 区间分别进行一次+1操作，考虑差分，我们只需要在分别在 \(l,l+1\dots r\) 的差分数组分别 \(+1\) 然后 \(r+1\) 的位置 \(-(r-l+1)\) 即可，直接线段树区间修改即可

查询时，用线段树直接区间查询前缀和即可

T9：

直接秒了

考虑它的合并过程就相当于是一棵线段树的合并过程，所以直接在线段树上模拟即可

因为单点修改只会影响到 \(logn\) 的点的答案，所以可以直接做

T10：

想了一会，也切了

考虑维护一个区间的左右括号个数和答案个数，然后合并两个区间时就用左区间的左括号去匹配右区间的右括号，相当于是简化版的T3

感觉线段树这一章都不是很难，做起来很舒服