分块
写在前面
非常简单的分块，使我开心的转圈，稍微看了一下 oi wiki 就懂了，妈妈再也不用担心我的暴力了
正文
分块，非常优雅的暴力，本质是上是通过对原数据的适当划分，并在划分后的每一个块上预处理部分信息，从而较一般的暴力算法取得更优的时间复杂度。
例如（博客萌新好不容易整的）：
\(n\) 如果不是s的倍数最后一个块可能不完整，但也没关系，对最后操作无影响
查询操作
如果负责查询的 \(l,r\) 都在同一个块中，暴力枚举 \(l\) 到 \(r\)
如果 \(l\) 或 \(r\) 不在所在块的头或尾，则暴力将 \(l\) 和 \(r\) 枚举到块的头或尾部
然后再从 \(l\) 所在的整块枚举整快到 \(r\) 所在的整块，将所有查询结果加和，即为结果
修改操作
和查询操作的思路一样
就是在整块修改时，无法依次修改块中元素，需要在修改时打个 \(add[]\) 标记，存储整块 \(k[]\) 的值被修改了，而单点 \(a[]\) 却没有被修改的数值，在查询单点 \(a[]\) 时加上标记就行
警示后人
在判断第 \(i\) 个数属于哪个块时，要注意对于任意一个块 \(k[j]\) （为了简单举 \(j=1\) 的例子）的下标为 \(1,2,3 \cdots,s\)
然而 \(1,2,3 \cdots,s-1\) 的下标 \(i\) 进行对应块的下标却为 \(\tfrac{i}{s}+1\) ，要记得特判
升级版分块
P2801 教主的魔法
就是多了一个区间查询大于等于 \(k\) 的个数
考虑对于一个整块，我们每次查询时，若它是无序的则排一个序，然后二分查找第一个大于等于的数就行了
代码
属于是一个失败，最后都不知道自己在写什么了，还是伟大的雪猫学长调了半个小时，找到了无数个锅之后，才总算AC了，啊，伟大%%%！！！
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
char op;
int s,n,q,cnt,l,r,w;
int k[N],a[N],b[N],add[N];
int id(int x){
if(x%s==0) return x/s;
return x/s+1;
}
void change(int x,int y,int ad){
if(id(x)==id(y)){
for(int i=x;i<=y;i++){
a[i]+=ad;
}
k[id(x)]=1;
return;
}
while(x%s!=1){
a[x]+=ad;
k[id(x)]=1;
x++;
}
while(y%s!=0){
a[y]+=ad;
k[id(y)]=1;
y--;//锅1，y减小不是增大
}
for(int i=id(x);i<=id(y);i++){
add[i]+=ad;
}
}
int query(int x,int y,int c){
int ans=0;
if(id(x)==id(y)){
for(int i=x;i<=y;i++){
if(a[i]+add[id(x)]>=c){
ans++;
}
}
return ans;
}
while(x%s!=1){
if(a[x]+add[id(x)]>=c){
ans++;
}
x++;
}
while(y%s!=0){
if(a[y]+add[id(y)]>=c){
ans++;
}
y--;//锅2，同锅1
}
for(int i=id(x);i<=id(y);i++){
if(k[i]){
for(int j=(i-1)*s+1;j<=min(i*s,n);j++){
b[j]=a[j];
}
sort(b+(i-1)*s+1,b+min(i*s+1,n+1));//锅3，sort起始位+1不是+2，考虑当i=1时值为1
//锅4，考虑越界
k[i]=0;
}
ans+=min(n+1,i*s+1)-(lower_bound(b+(i-1)*s+1,b+min(i*s+1,n+1),c-add[i])-b);//锅5，考虑lower_bound的用法
}
return ans;
}
int main(){
scanf("%d%d",&n,&q);
s=(int)sqrt(n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
if(i%s==1) cnt++;
b[i]=a[i];
}
for(int i=1;i<=cnt;i++) k[i]=1;
for(int i=1;i<=q;i++){
scanf(" %c %d%d%d",&op,&l,&r,&w);
if(op=='M'){
change(l,r,w);
}
else{
printf("%d\n",query(l,r,w));
}
}
}
ps:更新2024.12.28
本人重学分块，之前写的代码非常不优雅，于是又写了一篇很优雅的代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5,M=1e4+5;
int n,q,block,t;
int st[M],en[M],add[M],pos[N];
struct nm{
int a,id;
}a[N];
bool cmp(nm x,nm y){
return x.a<y.a;
}
void merge(int l,int r,int w){
int p=pos[l],q=pos[r];
if(p==q){
for(int i=st[p];i<=en[q];i++){
if(a[i].id<=r&&l<=a[i].id){
a[i].a+=w;
}
}
sort(a+st[p],a+en[q]+1,cmp);
}
else{
for(int i=p+1;i<=q-1;i++) add[i]+=w;
for(int i=st[p];i<=en[p];i++){
if(a[i].id<=r&&l<=a[i].id){
a[i].a+=w;
}
}
sort(a+st[p],a+en[p]+1,cmp);
for(int i=st[q];i<=en[q];i++){
if(a[i].id<=r&&l<=a[i].id){
a[i].a+=w;
}
}
sort(a+st[q],a+en[q]+1,cmp);
}
}
int dic(int x,int y,int c){
if(a[y].a<c) return 0;
int l=x,r=y;
while(l<r){
int mid=(l+r)>>1;
if(a[mid].a<c) l=mid+1;
else r=mid;
}
return y-l+1;
}
int query(int l,int r,int w){
int p=pos[l],q=pos[r],res=0;
if(p==q){
for(int i=st[p];i<=en[p];i++){
if(a[i].id<=r&&l<=a[i].id&&a[i].a>=w-add[p]) res++;
}
}
else{
for(int i=p+1;i<=q-1;i++){
res+=dic(st[i],en[i],w-add[i]);
}
for(int i=st[p];i<=en[p];i++){
if(a[i].id<=r&&l<=a[i].id&&a[i].a>=w-add[p]) res++;
}
for(int i=st[q];i<=en[q];i++){
if(a[i].id<=r&&l<=a[i].id&&a[i].a>=w-add[q]) res++;
}
}
return res;
}
int main(){
scanf("%d%d",&n,&q);
block=sqrt(n);
t=n/block;
if(n%block) t++;
for(int i=1;i<=t;i++){
st[i]=(i-1)*block+1;
en[i]=i*block;
}
en[t]=n;
for(int i=1;i<=n;i++){
scanf("%d",&a[i].a);
a[i].id=i;
pos[i]=(i-1)/block+1;
}
for(int i=1;i<=t;i++){
sort(a+st[i],a+en[i]+1,cmp);
}
for(int i=1;i<=q;i++){
char c[1];
int l,r,w;
scanf("%s%d%d%d",c,&l,&r,&w);
if(c[0]=='M'){
merge(l,r,w);
}
else{
printf("%d\n",query(l,r,w));
}
}
}
hdu5057
分块直接做就完了
按照每一位维护，然后就是分块板子
代码（没有测试，只通过了样例
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=400;
int n,m,T,block,t;
int a[10][N],num[10][10][M],pos[N],st[M],en[M];
void build(int x,int y){
for(int i=0;i<=9;i++){
int now=y%10;
y/=10;a[i][x]=now;
num[i][now][pos[x]]++;
}
}
void change(int x,int y){
for(int i=0;i<=9;i++){
int old=a[i][x],now=y%10;
y/=10;a[i][x]=now;
num[i][old][pos[x]]--;
num[i][now][pos[x]]++;
}
}
int query(int l,int r,int d,int g){
int p=pos[l],q=pos[r],res=0;
if(p==q){
for(int i=l;i<=r;i++){
if(a[d][i]==g) res++;
}
}
else{
for(int i=l;i<=en[p];i++){
if(a[d][i]==g) res++;
}
for(int i=st[q];i<=r;i++){
if(a[d][i]==g) res++;
}
for(int i=p+1;i<=q-1;i++){
res+=num[d][g][i];
}
}
return res;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m);
block=(int)sqrt(n);
t=n/block;
if(n%block) t++;
for(int i=1;i<=n;i++){
pos[i]=(i-1)/block+1;
}
for(int i=1;i<=t;i++){
st[i]=(i-1)*block+1;
en[i]=i*block;
}
en[t]=n;
for(int i=0;i<=9;i++){
for(int j=0;j<=9;j++){
for(int k=1;k<=t;k++){
num[i][j][k]=0;
}
}
}
for(int i=0;i<=9;i++){
for(int j=1;j<=n;j++){
a[i][j]=0;
}
}
for(int i=1;i<=n;i++){
int g;
scanf("%d",&g);
build(i,g);
}
for(int i=1;i<=m;i++){
char c[1];
int l,r,d,g;
scanf("%s",c);
if(c[0]=='Q'){
scanf("%d%d%d%d",&l,&r,&d,&g);
printf("%d\n",query(l,r,d-1,g));
}
else{
scanf("%d%d",&l,&g);
change(l,g);
}
}
}
}
P3203 弹飞绵羊
非常巧妙的转化
我们先考虑如暴力做的话如果查询 \(O(1)\) 修改就 \(O(n)\)，修改 \(O(1)\) 查询 \(O(n)\)，然后所以如果可以将两个操作都下降到 \(O(\sqrt n)\)，就可以解决了
所以考虑分块，我们对一个块内部做到修改 \(O(block)\)，查询\(O(1)\)（block为块长)
这样我们就可以查询时跳块，做到 \(O(t)\) （t为块个数）
因为分块 \(t,block\) 都是 \(O(\sqrt n)\) 量级的，所以就可以直接做到 \(O(m\sqrt n)\)
实现：
设 \(num[i]\) 表示绵羊从 \(i\) 跳出它所在的块所需要的弹跳次数，然后 \(to[i]\) 表示从 \(i\) 跳出它所在的块落到其它块的点
然后修改时对于整个块重新统计贡献，查询时一个一个往后跳
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=505;
int n,m,block,t;
int to[N],num[N],st[M],en[M],k[N],pos[N];
int query(int g){
int nxt=g,res=0;
while(nxt<=n){
res+=num[nxt];
nxt=to[nxt];
}
return res;
}
void opera(int i){
for(int j=en[i];j>=st[i];j--){
if(j+k[j]>en[i]){
num[j]=1;
to[j]=j+k[j];
}
else{
num[j]=num[j+k[j]]+1;
to[j]=to[j+k[j]];
}
}
}
void change(int x,int g){
k[x]=g;
int i=pos[x];
opera(i);
}
int main(){
scanf("%d",&n);
block=(int)sqrt(n);
t=n/block;
if(n%block) t++;
for(int i=1;i<=n;i++){
pos[i]=(i-1)/block+1;
}
for(int i=1;i<=t;i++){
st[i]=(i-1)*block+1;
en[i]=i*block;
}
en[t]=n;
for(int i=1;i<=n;i++){
scanf("%d",&k[i]);
}
for(int i=1;i<=t;i++){
opera(i);
}
scanf("%d",&m);
for(int i=1;i<=m;i++){
int op,q,k;
scanf("%d",&op);
if(op==1){
scanf("%d",&q);
q++;
printf("%d\n",query(q));
}
else{
scanf("%d%d",&q,&k);
q++;
change(q,k);
}
}
}
loj6279
给出一个长为n的数列，以及n个操作，操作涉及区间加法，询问区间内小于某个值x的前驱（比其小的最大元素）。
和正常的教主的魔法差不多，然后就转化一下就可以
loj6282
给出一个长为n的数列，以及n个操作，操作涉及单点插入，单点询问，数据随机生成。
因为是随机数据，可以直接做，在块里暴力插入，块与块之间暴力挨个找寻找下标
考虑不是随机数据怎么办，因为数据不随机，所以可以出现一直插在一个块中的情况，会炸
所以我们每插入 \(O(\sqrt n)\) 次，就重新平均分一下块，复杂度不会炸因为最多进行 \(O(\sqrt n)\) 次，每次操作复杂度 \(O(n)\)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=500;
int n,block,t,q;
int pos[N],a[N],en[M],num[M][N];
void allocate(){
block=(int)sqrt(n);
t=n/block;
if(n%block) t++;
for(int i=1;i<=t;i++){
en[i]=block;
}
if(n%block) en[t]=n%block;
for(int i=1;i<=n;i++){
pos[i]=(i-1)/block+1;
}
int id=1;
for(int i=1;i<=n;i++){
int p=pos[i];
num[p][id]=a[i];
id++;
if(i%block==0){
id=1;
}
}
}
void insert(int x,int r){
int now=0,p=0;
while(now<x){
p++;
now+=en[p];
}
now-=en[p];
int id=x-now;
// printf("%d %d\n",p,id);
for(int i=now+en[p];i>=id;i--){
num[p][i+1]=num[p][i];
}
num[p][id]=r;
en[p]++;
}
int query(int x){
int now=0,p=0;
while(now<x){
p++;
now+=en[p];
}
now-=en[p];
int id=x-now;
// printf("%d %d\n",p,id);
return num[p][id];
}
void remerge(){
n=0;
for(int i=1;i<=t;i++){
for(int j=1;j<=en[i];j++){
a[++n]=num[i][j];
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
allocate();
// for(int i=1;i<=n;i++){
// printf("%d ",pos[i]);
// }
// printf("\n");
q=n;
int re=sqrt(n);
for(int i=1;i<=q;i++){
int op,l,r,c;
scanf("%d%d%d%d",&op,&l,&r,&c);
if(op==0){
insert(l,r);
}
else{
printf("%d\n",query(r));
}
// for(int i=1;i<=t;i++){
// for(int j=1;j<=en[i];j++){
// printf("%d ",num[i][j]);
// }
// printf("\n");
// }
// printf("\n");
if(i%re==0){
remerge();
allocate();
}
}
}
P4145 上帝造题的七分钟 2 / 花神游历各国
首先观察到一个性质，就是一个数至多被开根6次就会变为0/1，所以我们只要对哪些不是0/1的块暴力修改，然后如果全都是0/1就跳过，复杂度一定是正确的
loj6284
也是一样的观察性质，一整块被改为1个数后我们就可以统一操作了，然后考虑散块怎么办，如果暴力修改的话，最劣复杂度是 \(O(n)\) 的
但是我们考虑对于一次修改操作，它最多只会破坏两个完整的块，也就是我们暴力修改的块的总数不会超过 3n 个，复杂度正确
P4168 [Violet] 蒲公英
非常巧妙的题，使我的大脑旋转
我们首先先对数列分块
然后我们考虑整块与散块的关系，因为我们想要知道整块要维护些什么，所以我们要知道众数的求法和整块散块的关系
一次区间查询操作会查到左右两边的散块，还有中间若干整块
考虑当众数在只出现在整块中的情况，那我们可以直接预处理得出（就是预处理出 \(mode[i][j]\) 表示在 \(i~j\) 之间的整块的众数），具体实现看我以下 preprocess 函数
若众数在散块中也出现过呢？
那么显然根据分块思想，我们将散块中所有出现过的值的出现次数与答案比较，然后更新答案即可
怎么算一个值出现的次数：
我们开个桶，表示这个值在散块中的出现次数，然后可以预处理出 \(s[i][j]\) 表示在 \(1~i\) 的整块中出现了多少次 j，然后前缀和计算，一个值出现的次数就是桶中的次数+ \(s[p+1][q-1]\)
因为我们要把值存在数组里，所以要离散化一下，然后还有输出时记得再把离散完的赋值回去（这个锅调了好久）
代码：
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=4e4+5,M=205;
int n,m,cnt,block,t;
int a[N],b[N],en[N],st[N],pos[N],mode[M][M],s[M][N],num[M][N],bar[N],id[N];
map<int,int>mp;
void dis(){
sort(b+1,b+1+n);
cnt=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=cnt;i++){
mp[b[i]]=i;
id[i]=b[i];
}
for(int i=1;i<=n;i++){
a[i]=mp[a[i]];
}
}
void allocate(){
block=(int)sqrt(n);
t=n/block;
if(n%block) t++;
for(int i=1;i<=t;i++){
st[i]=(i-1)*block+1;
en[i]=i*block;
}
en[t]=n;
for(int i=1;i<=n;i++){
pos[i]=(i-1)/block+1;
}
}
void preprocess(){
for(int i=1;i<=t;i++){
for(int j=st[i];j<=en[i];j++){
num[i][a[j]]++;
}
}
for(int i=1;i<=t;i++){
for(int j=1;j<=cnt;j++){
s[i][j]=s[i-1][j]+num[i][j];
}
}
for(int i=1;i<=t;i++){
for(int j=i;j<=t;j++){
mode[i][j]=mode[i][j-1];
for(int k=st[j];k<=en[j];k++){
bar[a[k]]++;
if(bar[a[k]]>bar[mode[i][j]]||(bar[a[k]]==bar[mode[i][j]]&&a[k]<mode[i][j])) mode[i][j]=a[k];
}
}
for(int j=0;j<=cnt;j++){
bar[j]=0;
}
}
}
bool compare(int x,int y,int p,int q){
int numx=bar[x]+s[q-1][x]-s[p][x],numy=bar[y]+s[q-1][y]-s[p][y];
if(numx>numy||(numx==numy&&x<y)) return 1;
return 0;
}
int query(int l,int r){
int p=pos[l],q=pos[r],res=0;
if(p==q){
for(int i=l;i<=r;i++){
bar[a[i]]++;
if(bar[a[i]]>bar[res]||(bar[a[i]]==bar[res]&&a[i]<res)) res=a[i];
}
for(int i=l;i<=r;i++) bar[a[i]]=0;
}
else{
res=mode[p+1][q-1];
for(int i=l;i<=en[p];i++){
bar[a[i]]++;
if(compare(a[i],res,p,q)) res=a[i];
}
for(int i=st[q];i<=r;i++){
bar[a[i]]++;
if(compare(a[i],res,p,q)) res=a[i];
}
for(int i=l;i<=en[p];i++) bar[a[i]]=0;
for(int i=st[q];i<=r;i++) bar[a[i]]=0;
}
return res;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
b[i]=a[i];
}
dis();
allocate();
preprocess();
int x=0;
for(int i=1;i<=m;i++){
int l,r;
scanf("%d%d",&l,&r);
l=(l+x-1)%n+1;
r=(r+x-1)%n+1;
if(l>r) swap(l,r);
x=id[query(l,r)];
printf("%d\n",x);
}
}
参考
P3870
我们维护一个add表示块整体进行翻转了几次，然后散块暴力反转翻转即可
P3396
想了好久，终于切了
根号分治题（话说不应该放在分块板块中）
对于模数在根号以内的数，我们暴力处理是 \(O(n)\) 的，无法接受，所以选择预处理 \(f[i][j]\) 表示当模数为 i 时，余数为 j 时的总和
对于模数在根号以外的数，就暴力查询
至于修改操作，只用修改根号以内的模数预处理出的答案即可
复杂度在 \(O((n+m)\sqrt n)\) 之内
P3863
非常巧妙的一题，首先我们考虑当序列中只有一个数的时候应该怎么办
我们可以对时间分一下块，然后加x就是将区间 \([t,q]\)（t为当前时间）加上x
查询就是查询 \([0,t)\) 的区间中有多少个数不小于x
然而现在又有了第二层的区间限制，怎么办呢？
考虑扫描线思想，我们从小到大枚举序列中的每个元素，考虑一次区间修改操作\([l,r]\)，就在处理l的时候将 \([t,q]\) 加上x，在处理r+1时 \([t,q]\) 减去x
也就是我们维护一个承载着修改操作的分块序列，对于一次查询，我们需要在查询时将所有数加上这一位的初始值（不是真加，形式上的加，为了在传递到下一位序列时不受影响）
然后就做完了
P1975
水紫，想到了一个听起来很正确的解法（没有验证），也算切了吧
我的思路是
应该是很正确的，复杂度也没有问题
然后正解做法更优雅，所以就写的正解
我们交换 \(x,y\) 那么对于 \(1~x-1,y+1~n\) 是没有影响的
所以我们只需要查询一下交换对 \(x+1,y-1\) 的影响
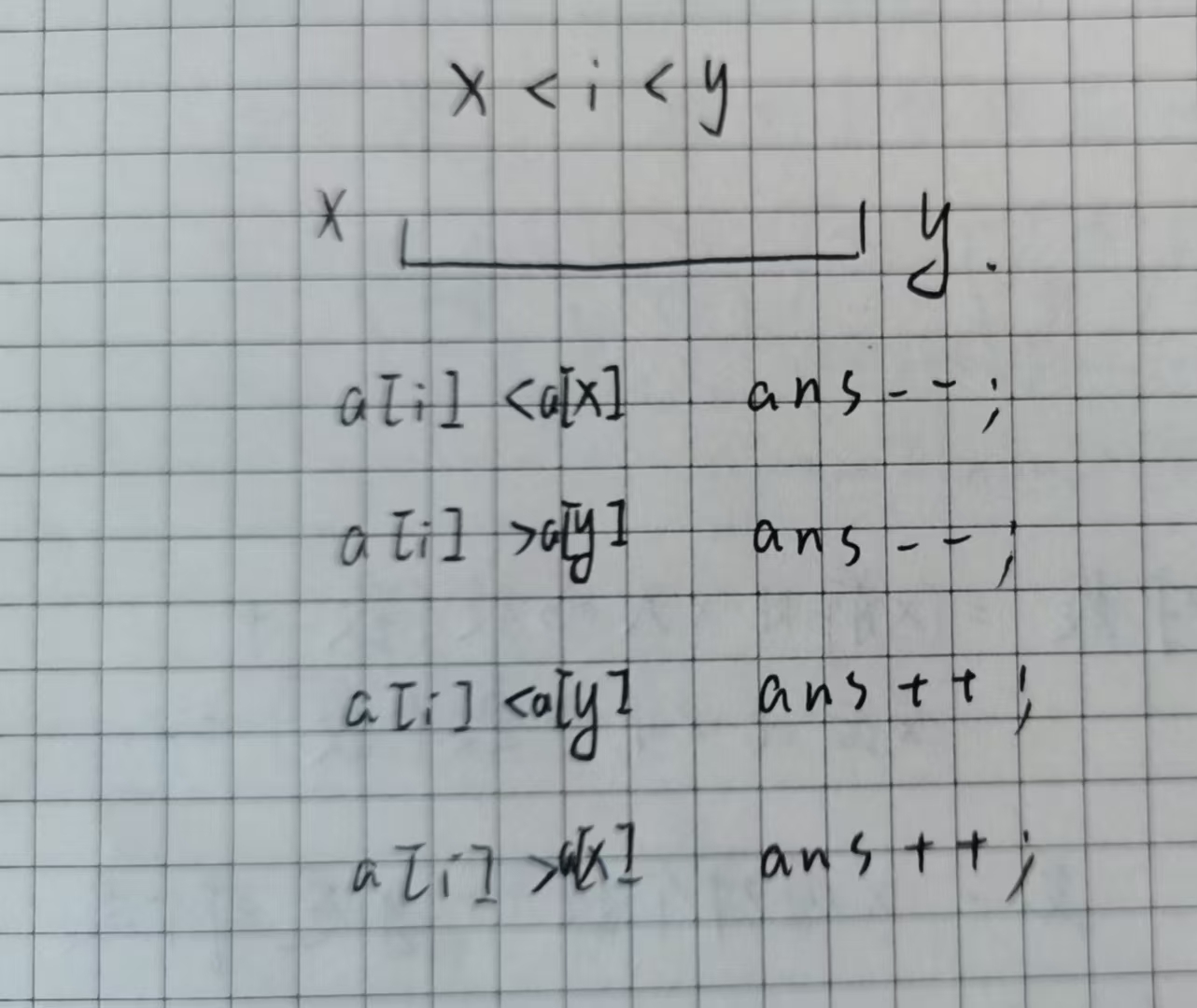
还要注意 \((x,y)\) 逆序对带来的影响，注：特判 \(a_x==a_y\)
还有就是注意要保证 \(x<y\)
浙公网安备 33010602011771号