tweedie损失函数

对于右偏长尾数据进行建模时，使用其他分布的损失函数（如对应高斯分布的MSE损失）效果可能不好。此时可考虑使用基于tweedie分布的损失函数进行建模。

 

tweedie分布

 tweedie分布式是一类特殊的指数衰减模型（exponential disperse model，EDM）。其方差和期望的关系如下，其中p是power参数，μ和Φ分别是期望和衰减参数。

tweedie分布的参数p决定了分布所属的子函数族，p=0为正态分布，p=1为泊松分布，p=2为伽马分布，p∈（1，2）时是泊松和伽马的混合分布。

 当分布式混合分布时，随机变量X ~ Tw(p, μ, ϕ)可表示为：

其pdf为：

 

其中 α(x, ϕ, p)是一个正则化项，保证分布是一个合法的pdf。

 

tweedie损失

对tweedie的pdf计算其负对数似然作为损失，那么

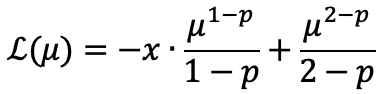
将μ作为估计量，那么

 

实现

import tensorflow as tf
def tweedie_loss_func(p):
    def tweedie_loglikelihood(y, y_hat):
        loss = - y * tf.pow(y_hat, 1 - p) / (1 - p) + \
               tf.pow(y_hat, 2 - p) / (2 - p)
        return tf.reduce_mean(loss)
return tweedie_loglikelihood

　　

参考链接

https://towardsdatascience.com/tweedie-loss-function-for-right-skewed-data-2c5ca470678f