LightGBM原理解析

摘要

本文对lgb的基本原理进行简要概括。

基于直方图的节点分裂

lgbm使用基于直方图的分裂点选择算法，分裂准则为最小化方差，也即最大化方差增益variance gain：

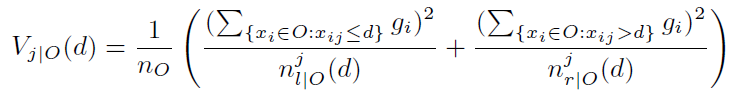
对比xgb的loss reduction：

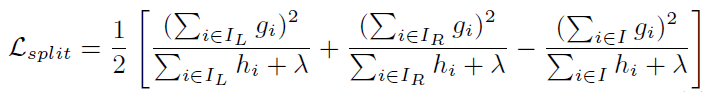
可以发现，两者是一致的，不同点在于，xgb的loss reduction包含了正则化因子λ，而lgbm未作正则化，因为lgbm的损失函数为均方误差，因此其二阶梯度hi=1，体现在loss reduction上，lgbm的分母为n（n=Σhi）。

因此，lgbm的均方误差实际是一种特例，其最优化方法仍然与xgb一致。仍然可以认为其对直方图统计了一阶和二阶梯度，其中，一阶梯度为，二阶梯度为。

方差增益的推导

我们考虑当前树中某个具体的结点，对于某个当前结点来说，定义当前结点上样本集合为 $O$ ，我们期望遍历所有候选特征以及候选分裂点，来找到一个特征j和对应的分裂点d，使得分裂当前结点以后左右子结点上的样本总体方差更小，转化为公式，就是使得 $\sum_{i\in O}(g_i-\bar{g})^2-\sum_{p\in L}(g_p-\bar{g}_L)^2-\sum_{q\in R}(g_q-\bar{g}_R)^2$ 最大，这个公式第一样式是指没分裂之前结点的均方误差，后面两项分别是分裂以后左右孩子结点的样本均方误差之和。

由于 $\sum_{i\in O}(g_i-\bar{g})^2$ 对于当前结点分裂增益的计算是个常量，上式即等同于最小化 $\sum_{p\in L}(g_p-\bar{g}_L)^2+\sum_{q\in R}(g_q-\bar{g}_R)^2$ 。

我们知道 $\sum_i(y_i-\bar{y})^2=\sum_iy^2_i-n\bar{y}^2$ ，那么上面式子进一步化简为 $\sum_{p\in L}g_p^2-n\bar{g_L}^2+\sum_{q\in R}g_q^2-m\bar{g_R}^2=\sum_{i\in O}g_i^2-(n\bar{g}_L^2+m\bar{g}_R^2)$ ，由于第一项又是一个常数项，因此我们的问题最终转化为最大化 $(n\bar{g}_L^2+m\bar{g}_R^2)$ ，进一步地再化简： $n\bar{g}_L^2+m\bar{g}_R^2=n(\frac{1}{n}\sum_{i\in L}g_i)^2+m(\frac{1}{m}\sum_{i\in R}g_i)^2=\frac{1}{n}(\sum_{i\in L}g_i)^2+\frac{1}{m}(\sum_{i\in R}g_i)^2$ ，这里结果就是Lightgbm中的variance gain，即最大化左右叶子结点样本负梯度和的平方。

第二种理解就是参考XGBoost的信息增益计算方式，这里我直接引用XGBoost里面的增益计算公式：

$\frac{(\sum_{i\in L} g_i)^2}{\sum_{i\in L}h_i+\lambda}+\frac{(\sum_{i\in R} g_i)^2}{\sum_{i\in R}h_i+\lambda}-\frac{(\sum_{i\in O} g_i)^2}{\sum_{i\in O}h_i+\lambda}$ ，同样地，第三项是个常数项，实际上就是在最大化前两项。对于GBDT使用平方误差作为损失函数来说，样本的二阶导数 $h_i$ 等于1（损失函数 $\frac{1}{2} \sum_i (\hat{y}_i-y_i)^2$ ），且忽略XGBoost中正则项系数 $\lambda$ ，就会得到和上述式子同样的结果。

基于梯度的单边采样（gradient-based one-side sampling, GOSS）

lgb采用基于梯度的单边采样（GOSS）减少样本数量。GOSS首先按照样本的梯度大小对数据进行降序排序，选取前a%的大梯度样本，然后从剩余的小梯度样本中采样b%，为保持样本分布不变，对小梯度样本加权(1-a)/b。

互斥特征绑定（exclusive feature bundling, EFB）

对于高维稀疏数据，很多特征之间都是互斥的，也就是对于同一个样本，不同特征通常不会同时取非零值。这样的性质给可以几乎无损失地减少特征数量提供了可能性。

EFB包括两个步骤：特征分簇和特征合并。

特征分簇：将每个特征视为一个节点，在非互斥节点之间添加边，将特征bundle问题转换为图着色问题，算法如下：

1、将特征作为节点，特征之间的冲突（两个特征同时非0的样本数量）作为边的权重，构建图；

2、按照节点度对特征进行降序排序；

3、按顺序遍历特征，将其加入已有bundle（若加入后bundle的冲突数小于阈值）或为其创建新的bundle；

算法3的时间复杂度是

特征合并：通过增加偏移量的方式，将多个互斥特征合并到同一个特征，例如特征A的取值范围为(0,10)，特征B的取值范围为(0,20)，那么可以为特征B增加偏移量10，合并后B的取值范围为(10,30)，新特征的取值范围为(0,30)。

具体如下：

离散特征处理

为解决one-hot编码处理类别特征的不足，lgb采用many vs many 的切分方式，实现类别特征的最优切分。

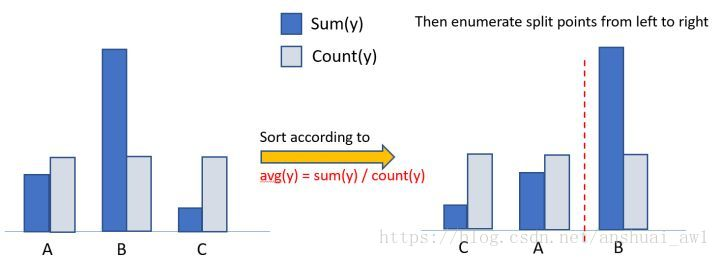
具体方式为：

1、离散特征建立直方图的过程：

统计该特征下每一种离散值出现的次数，并从高到低排序，并过滤掉出现次数较少的特征值, 然后为每一个特征值，建立一个bin容器, 对于在bin容器内出现次数较少的特征值直接过滤掉，不建立bin容器。

2、计算分裂阈值的过程：

2.1、先看该特征下划分出的bin容器的个数，如果bin容器的数量小于4，直接使用one vs other方式, 逐个扫描每一个bin容器，找出最佳分裂点;

2.2、对于bin容器较多的情况, 先进行过滤，只让子集合较大的bin容器参加划分阈值计算, 对每一个符合条件的bin容器进行公式计算(公式如下: 该bin容器下所有样本的一阶梯度之和 / 该bin容器下所有样本的二阶梯度之和 + 正则项(参数cat_smooth)，这里为什么不是label的均值呢？其实上例中只是为了便于理解，只针对了学习一棵树且是回归问题的情况，这时候一阶导数是Y, 二阶导数是1)，得到一个值，根据该值对bin容器从小到大进行排序，然后分从左到右、从右到左进行搜索，得到最优分裂阈值。但是有一点，没有搜索所有的bin容器，而是设定了一个搜索bin容器数量的上限值，程序中设定是32，即参数max_num_cat。

LightGBM中对离散特征实行的是many vs many 策略，这32个bin中最优划分的阈值的左边或者右边所有的bin容器就是一个many集合，而其他的bin容器就是另一个many集合。

2.3、对于连续特征，划分阈值只有一个，对于离散值可能会有多个划分阈值，每一个划分阈值对应着一个bin容器编号，当使用离散特征进行分裂时，只要数据样本对应的bin容器编号在这些阈值对应的bin集合之中，这条数据就加入分裂后的左子树，否则加入分裂后的右子树。

并行计算

lgbm的并行方式有三种，分别是特征并行、数据并行、投票并行（voting parallel）。

1、特征并行

传统的gbdt并行方法为：不同的worker存储不同的特征集，再找到全局的最佳分裂点后，具有该划分点的worker进行节点分裂，然后广播切分后的左右子树数据结果，其他worker收到结果后也进行广播；

而在lgbm中，每个worker保留了所有的特征集，在找到全局的最佳分割点后每个worker可自行进行划分，不再依赖广播，减少了网络通信，但存储代价变高；

2、数据并行

数据并行的目标是并行化整个决策过程。每个worker拥有部分数据，独立地构建局部直方图，合并后得到全局直方图，在全局直方图中寻找最优切分点。

3、投票并行

lgbm采用一种称为pv-tree的算法进行投票并行，本质上也是一种数据并行。pv-tree和普通的决策树差不多，只是在寻找最优切分点上有所不同。

每个worker拥有部分数据，独自构建数据并找到最优的k个划分特征，中心worker聚合得到最优的2k个划分特征，在想每个worker收集2k个直方图，进行合并得到最优化分，最后广播到每一个worker进行本地划分。

图着色代码

def matrix_graph(g, v_num):
    """生成二维矩阵"""
    return [[1 if col in g[row] else 0 for col in range(v_num)] for row in range(v_num)]
 
def nodes_inorder_des(m, v_num):
    """将结点按度数降序排好"""
    deg = {}
    for v in range(v_num):
        deg[v] = m[v].count(1)
    return sorted(deg, key=deg.get, reverse=True)
 
def graph_color(m, n, v_num):
    """将节点按照染色颜色划分"""
    painted = set()
    res = list()
    for v in n:
        if v not in painted:  # 每次找未着色的点
            group = list([v])  # 保存相同颜色的结点
            painted.add(v)
            for v_other in range(v_num):
                if m[v][v_other] == 0 and v_other not in painted:  # v与v_other不邻接 and 其邻接点没有被染色
                    if all(m[v_group][v_other] == 0 for v_group in  # v_other与同组节点不邻接
                           group[1:]):  # 拷贝group,保持不变性,并且从新加入节点开始比较
                        painted.add(v_other)
                        group.append(v_other)
            res.append(group)
 
            if len(painted) == total_v_num:
                break
    return res
 
if __name__ == '__main__':
    total_v_num = len(graph)
 
    matrix = matrix_graph(graph, total_v_num)
 
    nodes = nodes_inorder_des(matrix, total_v_num)
 
    res = graph_color(matrix, nodes, total_v_num)
 
    print('染色情况:', res)
    print('染色数:', len(res))

参考链接

https://www.microsoft.com/en-us/research/wp-content/uploads/2017/11/lightgbm.pdf

https://papers.nips.cc/paper/2017/hash/6449f44a102fde848669bdd9eb6b76fa-Abstract.html

https://blog.csdn.net/anshuai_aw1/article/details/83275299

https://www.zhihu.com/question/386159856/answer/1145984790

https://blog.csdn.net/qq_43658387/article/details/103129196

https://blog.csdn.net/csg3140100993/article/details/107813598

posted @ 2021-05-13 15:04 zcsh 阅读(1642) 评论(0) 编辑收藏举报

刷新页面返回顶部

LightGBM原理解析

公告