【转】风控中的特征评价指标(一)——IV和WOE
转自:https://zhuanlan.zhihu.com/p/78809853
1、IV值的用途
IV,即信息价值(Information Value),也称信息量。
目前还只是在对LR建模时用到过这两个关键指标,当我们使用决策树时可以通过限制树的深度间接筛选掉一些对于当前任务贡献比较小的变量, 而LR则是给多少变量就使用多少变量(L2正则下)。通常我们为了保证模型的有效性以及数据的全面性,在特征工程中会尽可能多的提供特征变量,包括衍生变量,这些衍生变量不会全部进入模型进行训练,否则模型会因为过多相关变量显得不稳定,也会增加运算的复杂性。那么应该如何选择什么变量可以进入模型呢?一般来说有主要根据5点:
1)变量的预测能力(贡献值)
2)变量的鲁棒性(稳定性)
3)变量的可解释性
4)变量的可行性
5)变量的相关性
IV值就是用来衡量变量预测能力的,IV值越大,表示该变量的预测能力越强。类似的指标还有信息增益、基尼系数等。
2、IV值的计算
为了介绍IV的计算方法,我们首先需要认识和理解另一个概念——WOE,因为IV的计算是以WOE为基础的。
2.1 WOE的概念及计算
WOE,即证据权重(Weight of Evidence),WOE 是对原始自变量的一种编码形式。要对一个变量进行 WOE 编码,需要首先把这个变量进行分组处理(也叫离散化、分箱),分组后,对于第i组,WOE的计算公式如下:
是该组中响应客户在该组中的比例;
是该组中未响应客户在该组中的比例;
是该组中响应客户数据量;
是该组中该组中未响应客户数据量;
是该组中响应客户总数据量;
是该组中未响应客户总数据量。响应客户指正样本,未响应客户指负样本。
以上公式表示,WOE实际上是“当前分组中响应客户占所有响应客户的比例”和“当前分组中没有响应的客户占所有没有响应的客户的比例”的差异。
对这个公式做一个简单变换,可以得到:
变换以后含义更明显,可以理解为当前组中正负样本的比值,与所有样本中正负样本比值的差异。这个差异是用这两个比值的比值,再取对数来表示的。差异越大,WOE越大,这个分组里的样本响应的可能性就越大,差异越小,WOE越小,这个分组里的样本响应的可能性就越小。WOE可能为负,但其绝对值越大,对于分类贡献越大。当分箱中正负的比例等于随机(大盘)正负样本的比值时,说明这个分箱没有预测能力,即WOE=0。
2.2 IV值的计算
对于一个分组后的变量,第i组的WOE已经介绍过,同样,对于分组i,也会有一个对应的IV值,计算公式如下:
IV值在WOE的基础上保证了结果非负。
根据变量在各分组上的IV值,得到整个变量的IV值为:
为变量分组个数
WOE可能为负值,IV值不可能为负,根据IV值选择变量后,用WOE替换变量各分组的值进入模型。
3、如何根据IV值评估变量预测能力
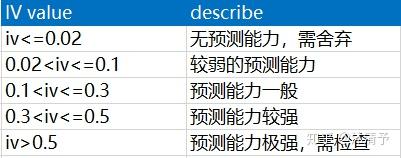
一般我们选择 IV值大于0.02的那些变量进入模型。 如果IV值大于 0.5 ,改变量就是属于过预测变量,通常被选座分群变量,将样本拆分成多个群体,针对不同的群体分别开发模型。
4、关于IV和WOE的进一步思考
4.1 为什么用IV而不是直接用WOE
从上面的内容来看,变量各分组的WOE和IV都隐含着这个分组对目标变量的预测能力这样的意义。那我们为什么不直接用WOE相加或者绝对值相加作为衡量一个变量整体预测能力的指标呢?
IV和WOE的差别在于IV在WOE基础上乘以的那个(pyi-pni),我们暂且用pyn来代表这个值。
第一个原因,当我们衡量一个变量的预测能力时,我们所使用的指标值不应该是负数。从这个角度讲,乘以pyn这个系数,保证了变量每个分组的结果都是非负数,可以验证一下,当一个分组的WOE是正数时,pyn也是正数,当一个分组的WOE是负数时,pyn也是负数,而当一个分组的WOE=0时,pyn也是0。当然,上面的原因不是最主要的,因为其实WOE的绝对值也可以完全避免负数的出现。
更主要的原因,也就是第二个原因是,乘以pyn后,体现出了变量当前分组中个体的数量占整体个体数量的比例,对变量预测能力的影响。即当各分组样本分布不均匀时对其预测能力的影响。
假设一个营销响应模型中,有变量A,其取值只有两个:0,1,数据如下:

从上表可以看出,当变量A取值1时,其响应比例达到了90%,非常的高,但是我们能否说变量A的预测能力非常强呢?不能。为什么呢?原因就在于,A取1时,响应比例虽然很高,但这个分组的客户数太少了,占的比例太低了。虽然,如果一个客户在A这个变量上取1,那他有90%的响应可能性,但是一个客户变量A取1的可能性本身就非常的低。所以,对于样本整体来说,变量的预测能力并没有那么强。我们分别看一下变量各分组和整体的WOE,IV。

从这个表我们可以看到,变量取1时,响应比达到90%,对应的WOE很高,但对应的IV却很低,原因就在于IV在WOE的前面乘以了一个系数,而这个系数很好的考虑了这个分组中样本占整体样本的比例,比例越低,这个分组对变量整体预测能力的贡献越低。相反,如果直接用WOE的绝对值加和,会得到一个很高的指标,这是不合理的。
4.2 IV的其他情况以及处理方式
1)如果IV很小不一定是变量的预测能力很差,如4.1所述,如果某个变量饱和度很低,或者分组区分明显的组别所占比例很小,那么 IV 也会响应较小
解决方法:尝试重新对变量分组后查看IV值
2)当样本中为0正例或0负例时,时 IV 值是+∞,这两个极端都是没有意义的,不能与正常 iV进行比较;
解决方法: 1.如果可能,直接把这个分组做成一个规则,作为模型的前置条件或补充条件;2.重新对变量进行离散化或分组,使每个分组的响应比例都不为0且不为100%,尤其是当一个分组个体数很小时(比如小于100个),强烈建议这样做,因为本身把一个分组个体数弄得很小就不是太合理。3.如果上面两种方法都无法使用,建议人工把该分组的响应数和非响应的数量进行一定的调整。如果响应数原本为0,可以人工调整响应数为1,如果非响应数原本为0,可以人工调整非响应数为1.
3)每个变量分组内响应和未响应的比例与样本整体的响应和未响应的比例差异越大,iV 值越大,当其相等时IV值为0;
4) 除非分组规则改变,组间的先后排序和目标变量的对调都不会影响IV 值;
5) WOE可以给变量的每个分组进行赋值,赋值过后的逻辑回归模型系数应该全部为正数,这是因为 WOE 值已经考虑了该组的正负贡献。
5、python代码
def bin_woe(tar, var, n=None, cat=None):
"""
连续自变量分箱,woe,iv变换
tar:target目标变量
var:进行woe,iv转换的自变量
n:分组数量
"""
total_bad = tar.sum()
total_good =tar.count()-total_bad
totalRate = total_good/total_bad
if cat == 's':
msheet = pd.DataFrame({tar.name:tar,var.name:var,'var_bins':pd.qcut(var, n, duplicates='drop')})
grouped = msheet.groupby(['var_bins'])
elif (cat == 'd') and (n is None):
msheet = pd.DataFrame({tar.name:tar,var.name:var})
grouped = msheet.groupby([var.name])
groupBad = grouped.sum()[tar.name]
groupTotal = grouped.count()[tar.name]
groupGood = groupTotal - groupBad
groupRate = groupGood/groupBad
groupBadRate = groupBad/groupTotal
groupGoodRate = groupGood/groupTotal
woe = np.log(groupRate/totalRate)
iv = np.sum((groupGood/total_good-groupBad/total_bad)*woe)
if cat == 's':
new_var, cut = pd.qcut(var, n, duplicates='drop',retbins=True, labels=woe.tolist())
elif cat == 'd':
dictmap = {}
for x in woe.index:
dictmap[x] 
