基于蒙特卡洛树搜索(MCTS)的多维可加性指标的异常根因定位
摘要:本文是我在从事AIOps研发工作中做的基于MCTS的多维可加性指标的异常根因定位方案,方案基于清华大学AIOPs实验室提出的Hotspot算法,在此基础上做了适当的修改。
1 概述
1.1 研究对象
拥有多维度属性(如省份、运营商、数据中心)的可加性KPI,如页面访问量。
1.2 要解决的问题
对KPI总量(如总页面访问量)进行监控,如果监测到异常,希望快速定位到导致该异常的是哪一个或那几个维度值组合(根因集合),如(北京,移动)或者(上海,联通)或者{(北京,移动),(上海,联通)}。
1.3 整体构成
由两部分组成:异常检测组件和根因定位组件。
2 异常检测组件
2.1 实现机制
异常检测组件主要分为3个部分:总KPI预测、异常检测和最细粒度KPI预测。
2.1.1 总KPI预测
利用历史数据对当前时间的总KPI值的上下边界进行预测。
输入:历史数据。
输出:总KPI上下边界的预测值。
2.1.2 异常检测
判断总KPI的真实值是否落在总KPI预测模块输出的上下边界范围之内,如果落在此范围内,认为正常,不进行下一步动作,检测结束;否则,认为发生了异常,进一步调用最细粒度KPI预测模块对每一个最细粒度的KPI进行预测,预测结果作为根因定位的输入,最细粒度KPI预测完成之后,触发根因定位。
输入:总KPI的上下边界预测值、历史数据。
输出:总KPI是否异常、异常点(如果异常)。
2.1.3 最细粒度KPI预测
根据历史数据对每一个最细粒度的KPI的值进行预测。
输入:历史数据。
输出:每一个最细粒度的KPI的预测值。
3 根因定位组件
如果异常检测组件检测到总KPI发生了异常,该组件立即对所有最细粒度KPI进行预测。然后触发根因定位组件对异常点进行定位,根因定位组件以Hotspot算法为基础。
3.1 Hotspot算法原理
3.1.1 几个重要的概念
元素:维度值的组合构成元素,如(北京)、(联通)、(北京,联通)。
后代元素:(北京,联通)是(北京)的后代元素,也是(联通)的后代元素。
Cuboid:从不同的维度观察数据所形成的数据立方体,例如数据共包括P、I、D三个维度,可以从单个维度观察数据如(P)、(I)、(D),也可以从多个维度观察数据,如(P,I)、(P,D)、(I,D)、(P,I,D)。不同的数据立方体对应不同粒度的元素。例如,(北京,联通)对应的cuboid是(P,I)。
父/子cuboid:例如(P)是(P,I)的父cuboid。父cuboid的数据可由子cuboid的数据聚合得到。
节点:指的是树的节点,主体是一个元素集合。主要包括以下几部分:
节点状态:该节点的元素集合,如(e1,e2)。
节点ps值:节点的ps值可近似看作该节点是根因节点的可能性。
节点Q值:节点的Q值指的是,以该节点为根节点的子树的所有节点中最大的ps值,它衡量的是,在树搜索的节点选择过程中,选择该节点的潜在价值。
节点访问次数N:树搜索过程中总共访问过某节点的次数。
父/子节点:向节点的元素集合中添加集合中没有的其他元素就构成该节点的子节点。例如,(e1,e2)是(e1)的子节点。
3.1.2 Potential score
3.1.2.1 Ripple effect
三个需要区分的概念:
真实值向量real:最细粒度元素的真实KPI值。
预测值向量forecast:通过历史数据预测得到的最细粒度的KPI值。
推导值向量deduced:在考察元素(集)为根因元素(集)的可能性时,将该元素(集)的变化值(真实值-预测值)通过ripple effect向下传导至所有它的最细粒度后代元素,其余最细粒度元素的推导值保持为预测值不变,以此构成最细粒度元素的推导值向量。
Ripple effect(连锁反应)描述了根因节点的KPI变化如何传播到其他元素。它的目的是,当我们假定一个元素发生了异常时,那么该元素的所有子元素都应该发生相应的变化,需要将该元素的变化量(真实值-预测值)按(预测值的)比例分配给它的所有最细粒度后代元素,计算其所有最细粒度后代元素的推导值。
例如,假设数据只有两个维度,地区和ISP。在考察beijing是根因元素的可能性时,需将beijing的变化量向下分配,如果:
real(beijing)=real(beijing,unicom)+real(beijing,mobile)=60+40=100
forecast(beijing)=forecast(beijing,unicom)+forecast(beijing,mobile)=100+100=200
那么,beijing的变化量为:
diff(beijing)=100-200=-100
(beijing,unicom)的推导值为:
deduced(beijing,unicom) = forecast(beijing,unicom) + diff(beijing) * forecast(beijing,unicom) / forecast(beijing) = 100-100*100/200 = 50
类似地,(beijing,mobile)的推导值为50。
而其余非(beijing)子元素的最细粒度子元素的推导值等于其预测值,例如:
deduced(shanghai,unicom) = forecast(shanghai,unicom)
3.1.2.2 Potential score
通过比较推导值向量和真实值向量的相似性(欧式距离)来确定被考察的元素集是根因的可能性,推导值和真实值之间的距离越小,代表被考察元素集越可能是根因集。
ps值就是一个衡量这种可能性的指标,ps值的定义为:
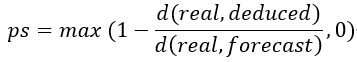
3.1.3 MCTS
根因定位的目标是将异常点定位到某个元素集合,并且这个元素集合只能来自同一个cuboid(是同一个cuboid元素集合的子集)。
以“用户体验监控异常影响人次”业务场景为例,共包括5个维度:I、E、C、P、L,五个维度的全组合可以分为五层,分别是:
第一层:I、E、C、P、L共5个组合;
第二层:(I,E)、(I,C)、(I,P)、(I,L)、(E,C)、……共10个组合;
第三层:(I,E,C)、(I,E,P)、(I,E,L)、(I,C,P)、(I,C,L)、……共10个组合;
第四层:(I,E,C,P)、(I,E,C,L)、……共5个组合;
第五层:(I、E、C、P、L)共1个组合。
仅考虑最下层的cuboid,其所有维度值的组合超过了220万元素。如果考虑这220万个元素的任意组合,共构成22200000-1种组合(不包括空集),要遍历这么多的组合,计算每一个组合是根因集的“可能性”是不可能的,因此希望通过蒙特卡罗树搜索的方法来启发性地搜索最可能的组合。
标准的MCTS过程分为4个步骤:selection、expansion、simulation和back propagation。
本算法将MCTS过程分为以下5个步骤:pruning、selection、expansion、evaluation和back propagation。
3.1.3.1 Pruning
为了缩小搜索空间和减少计算量,在标准MCTS的基础上增加剪枝操作。
所谓剪枝,就是对MCTree的cuboid所拥有的元素集合进行删减,例如,如果将某个cuboid的元素数量从100减少到50,那么搜索空间就从2^100-1缩小到2^50-1,并且也会节省一部分计算。
方法是根据上层MCTree的搜索结果,对下层MCTree的元素进行裁剪。上层MCTree搜索结束后,会为每个MCTree(cuboid)生成一个最佳元组集,所有cuboid的最佳元素集构成一个更大的该层最佳元素总集,如果下层某个cuboid的某个元素不是上层最佳元素总集中任何元素的后代元素,那么认为该元素不具有成为根因的潜力,将其从它的cuboid元素集中删除,搜索过程不再对其加以考虑。
例如,考虑由地区和ISP两个维度构成的数据,地区维度包括两个值:北京和西藏,ISP维度包括两个值:移动和联通。那么构成2层3个cuboid:
第一层:(地区)cuboid、(ISP)cuboid;
第二层:(地区,ISP)cuboid。
并且(地区)cuboid和(ISP)cuboid均为(地区,ISP)cuboid的父cuboid。
对于(地区,ISP)这个cuboid,它由4个元素构成,分别是:(北京,联通)、(北京,移动)、(西藏,联通)、(西藏,移动)。(地区,ISP)cuboid的父cuboid分别是(地区)cuboid和(ISP)cuboid。因为搜索分层进行,所以先对(地区)cuboid和(ISP)cuboid进行搜索,然后根据该层的搜索结果对下层的(地区,ISP)cuboid进行剪枝,假设:
(地区)cuboid的最佳元素集合是{北京};
(ISP)cuboid的最佳元组集合为{移动}。
现在对(地区,ISP)cuboid进行剪枝。因为元素(西藏,联通)既不是“北京”的后代元素,也不是“移动”后代元素,所以认为它不具有作为根因的潜力,将其从(地区,ISP)cuboid的元素集合中剔除,之后只对剩余3个元素执行搜索。这样就完成了对(地区、ISP)cuboid(也或者说是(地区、ISP)MCTree)的剪枝。这样,搜索空间就从2^4-1=15降低到了2^3-1=7。
因为第一层不存在上层搜索结果,所以第一层不剪枝。
3.1.3.2 UCB准则
UCB准则为树搜索过程中节点的选择提供了一种“探索-利用”(exploration-exploitation)的平衡策略。
在选择过程中,如果面临从父节点的一组子节点中进行选择时,需要综合考虑对已探索的高Q值节点的优先利用,同时又要兼顾对部分探索较少的节点进行更多探索,以发现更多可能性。
假设当前节点为n0,它的子节点集合为children(n0),那么如果要从当前节点的子节点中选择一个作为当前节点,应该选择使得以下分数最大的子节点:
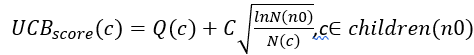
上式中, 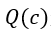 是子节点c的Q值,代表了exploitation因子,
是子节点c的Q值,代表了exploitation因子, 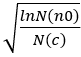 代表了exploration因子,C是exploration-exploitation的平衡因子,可以设置,论文建议值为
代表了exploration因子,C是exploration-exploitation的平衡因子,可以设置,论文建议值为  。
。
该式的含义是,随着父节点n0的访问次数的增加,访问次数较少的子节点c的exploration因子会变大,UCB算法将使得平衡向该子节点倾斜。
假如从当前节点n0的两个子节点c1、c2中选择一个节点,在初始时, 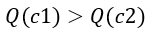 ,且
,且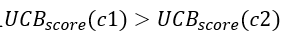 ,因此在一开始进行选择的时候,会不断选择出c1,但是随着N(n0)以及N(c1)的增长,两个子节点的UCB分数的差距会越来越小,最终导致
,因此在一开始进行选择的时候,会不断选择出c1,但是随着N(n0)以及N(c1)的增长,两个子节点的UCB分数的差距会越来越小,最终导致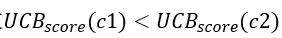 ,当再次选择时,就会选择出c2。
,当再次选择时,就会选择出c2。
3.1.3.3 Selection
Selection的目的是从当前已长成的树中选择一个已有的节点进行扩展,注意,选择出的节点必须是可扩展的,否则就无法再向其中添加新的元素构成子节点了。最初始的树由一个根节点构成,根节点是一个空集。
每次select均从根节点开始,从当前已长成的树中选择一个未完全扩展节点,在该节点上进行expand。
Select的原则是:1)如果当前节点的子节点已完全扩展,那么使用UCB准则选择一个子节点作为当前节点,并进一步迭代select过程,直到选择了一个叶节点;2)如果当前节点的子节点未完全扩展,此时不能直接使用UCB准则,那么依概率选择,①继续选择它的子节点,或者②返回当前节点。如果选择了①,那么和1)的情况一致,继续使用UCB准则,迭代select过程直至选择了一个叶节点,如果选择了②,那么返回该节点作为select的结果进行expand。
上述依概率选择的具体做法是:找到当前节点的所有子节点的Q值中的最大值Qmax,然后在(0,1)区间random一个随机数r,如果r<Qmax,选择①,反之,选择②。节点的Q值代表了该节点及其所有后代节点的ps值的最大值。
因为情况1)和情况2).①都需要继续迭代,只有情况2).②会返回当前节点作为select的结果,因此select过程最终都会落入2).②,除非树已经完全长成(如果树已经完全长成,则不再继续搜索)。
例如,假设某个cuboid只由两个元素e1、e2构成。针对以上几种情况的例子,选择以及扩展过程分别如下:
1)、假设树的当前状态如下:
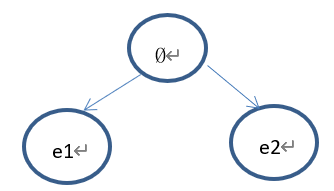
Select的过程如下:首先从根节点(Ø)开始,因为根节点已经完全扩展,所以使用UCB准则选择节点(e1)或者节点(e2),假设UCB(e1)>UCB(e2),那么选择节点(e1),因为节点(e1)没有子节点,那么依概率1选择返回该节点,因此select的结果为节点(e1)。
下一步拓展出来的节点为(e1,e2)。树的状态如下:
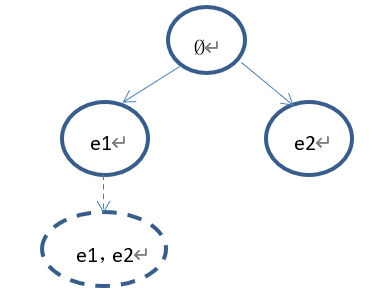
2)、假设当前树的状态如下:
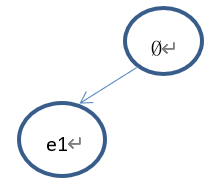
Select的过程如下:从根节点(Ø)开始,因为根节点的子节点还没有完全扩展(节点(e2)未扩展),因此依概率选择:①继续选择节点(e1);②返回根节点。
①如果选择了节点(e1),因为(e1)未完全扩展,且(e1)没有子节点,所以(依概率1)返回节点(e1)进行扩展。
下一步拓展出来的节点为(e1,e2)。树的状态如下:
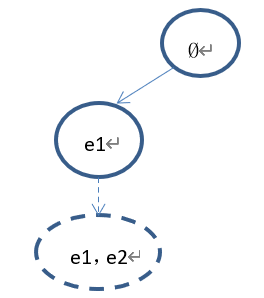
②如果返回根节点进行扩展。
下一步拓展出来的节点为(e2)。树的状态如下:
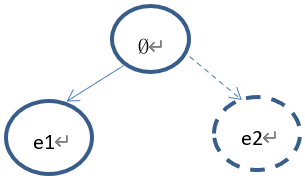
3.1.3.4 Expansion
对于已经选择出的节点,为其拓展新的子节点,新节点的元素集在继承其父节点的元素集的基础上,从剩余元素中选择ps值最大的元素加入。
例如,(地区)cuboid包含4个元素:北京、上海、广东、江苏。如果选择出了节点{(北京),(上海)},那么在拓展该节点时,比较(广东)和(江苏)的ps值,如果ps(广东)>ps(江苏),那么将(广东)加入新节点的元素集合,那么新节点为(北京,上海,广东)。
3.1.3.5 Evaluation
Evaluation对应于标准MCTS算法的simulation。用于计算新扩展节点的ps值,新节点的Q值等于其ps值。
3.1.3.6 Backup
在完成evaluation之后,需对新扩展节点所在路径上的所有节点的Q值和访问次数N进行更新。即对该路径上所有节点的访问次数+1;对每一个该路径上的节点node,如果Q(node)<Q(new_node),那么Q(node)=Q(new_node)。
Q值和ps值的区别是,ps值表征了一个节点是根因的可能性,Q值作为选择过程的依据,是当前节点及其所有子节点中最大的ps值,表征了选择该节点可能带来的最大回报。
3.2 实现机制
Hotspot算法的主要包括以下几个过程:维度值剪裁、构建cuboid集合、构建蒙特卡罗树集合、蒙特卡罗树并行搜索、根因选择。
3.2.1 维度值剪裁
如果在全量数据上直接执行Hotspot,会导致极大的计算压力。以目前使用的“用户体验监控异常影响人次”业务场景为例。
首先,所有维度值总共构成超过220万种组合,数量巨大,而Hotspot算法的计算又较为复杂,这会导致非常巨大的计算量;其次,当前场景的数据十分稀疏,在220万种场景组合里只有几千个组合是有数据的,其余的组合全部为0,这些数值为0的和数值非常小(相对于KPI总量)的数据几乎不会对总KPI的变化产生影响,因此我们认为它们不可能是总KPI异常的根因,将这一部分组合加入到计算的意义不大,反而会带来极大的计算压力,因此有必要在运用Hotspot算法实施根因定位之前,先对一部分的维度值进行剪裁。例如:
real(total)-forecast(total)=1e6
real(西藏)-forecast(西藏)=10
real(产品n)-forecast(产品n)=20
那么可以认为地区为“西藏”,以及产品为“产品n”的这部分变化量几乎不对总KPI变化量产生贡献,也就不可能是导致总KPI异常的根因。因此将“西藏”从“地区”维度移除,将“产品n”从“产品”维度移除。
通过这样的方式,可以在基本不对定位精度产生影响的前提下,大幅度地降低维度值的组合,减少计算量。
这实际上和Hotspot算法中的剪枝操作类似,只不过在大数据量的情况下,剪枝对计算量的压缩有限,维度值剪裁方法可以更大幅度地压缩计算量。
算法中采用的维度值裁剪的方法为:
1、设置维度裁剪的阈值thresh,例如0. 1。
2、计算总KPI的变化量的绝对值:
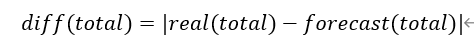
3、对于每一个维度dim,计算该维度的每一个维度值dim_value之下的最细粒度KPI变化量的绝对值之和。
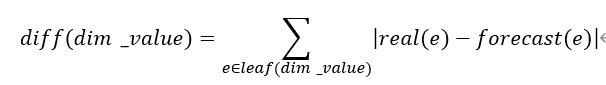
使用绝对值之和可以让维度值裁剪更加保守。
4、对于每一个维度dim,对于每一个该维度的维度值dim_value,如果:
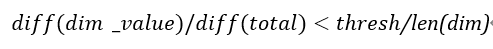
那么,将dim_value从dim中移除。
例如:以“地区”和“ISP”构成的二维数据为例。对“地区”维度, “北京”的最细粒度KPI的变化量的绝对值之和的计算如下:
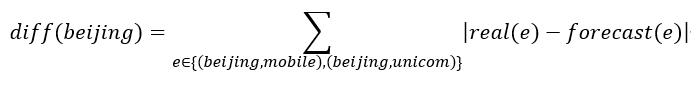
输入:当前时刻的最细粒度KPI真实值、预测值。
输出:经过剪裁后的各个维度的维度取值。
3.2.2 构建cuboid集合
Hotspot算法在每一个cuboid中进行搜索,因此定义了cuboid类,并实例化一个cuboid集合。
以“用户体验监控异常影响人次”业务场景为例,共包括5个维度:I、E、C、P、L,五个维度的全组合可以分为五层,分别是:
第一层:I、E、C、P、L共5个组合;
第二层:(I,E)、(I,C)、(I,P)、(I,L)、(E,C)、……共10个组合;
第三层:(I,E,C)、(I,E,P)、(I,E,L)、(I,C,P)、(I,C,L)、……共10个组合;
第四层:(I,E,C,P)、(I,E,C,L)、……共5个组合;
第五层:(I、E、C、P、L)共1个组合。
以上每一个组合对应一个cuboid实例,因此共有5层31个cuboid实例。蒙特卡罗树搜索在每一个cuboid实例内部进行。对于每一个cuboid实例,对最细粒度KPI真实值(dataframe)和预测值(dataframe)使用groupby().sum()聚合,得到该cuboid所包含的所有元素的真实值(dataframe)和预测值(dataframe)。
有了当前粒度的所有元素,就可以对这些元素使用MCTS找出最佳的元素组合了。
输入:经过剪裁后的各个维度的取值、最细粒度KPI真实值和预测值。
输出:cuboid实例集合。
3.2.3 构建蒙特卡罗树集合
定义了MCTree类。在MCTree类中实现了MCTS的几个步骤:prune、select、expand、evaluate、backup。
使用上一步创建的每一个cuboid实例,初始化一个蒙特卡罗树实例,cuboid作为MCTree的一个属性。所有的蒙特卡罗树实例构成一个和cuboid集合的结构完全一致的集合,分为5层,共31个实例。MCTree实例是MCTS的操作对象。
输入:cuboid集合。
输出:初始蒙特卡罗树集合。
3.2.4 并行蒙特卡罗树搜索(MCTS)
MCTS的目的是:从当前搜索的cuboid的元素全集中选择一个子集作为该cuboid的最佳集合。例如,对于(地区)cuboid,其元素全集为{北京,上海、新疆、西藏},经过MCTS后选择了子集{北京,上海}作为(地区)cuboid的最佳集合。
逐层对以上构建的蒙特卡罗树进行搜索,由于剪枝的需要,搜索过程层间串行、层内多进程并行,因此,对于“用户体验监控异常影响人次”业务场景,最多会同时对10棵树进行并行搜索。
输入:初始蒙特卡罗树集合。
输出:搜索后的蒙特卡罗树集合。
3.2.5 根因选择
比较每一棵树的最佳节点的ps值,选择ps值最大的的节点作为根因节点。
输入:搜索后的蒙特卡罗树集合。
输出:根因元素集合。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号