基于概率建模的多维时间序列的异常检测
摘要:亚马逊提出的deepar算法基于seq2seq模型对单维时间序列进行建模、预测,基于预测结果对时间序列中的异常点进行识别,但这种方法不适用于多维度的时间序列建模。在利用IoT+AI对现实世界中的物理设备进行异常检测的过程中,一个设备的运转/健康状态往往是由一系列指标共同决定的,指标之间并非相互独立的关系。本文吸收deepar算法的概率建模思想,以电机设备为例,提出一个对多维度指标进行异常检测的神经网络算法。
主要原理:
1、使用编码器将多维度时间序列编码为一个语义向量,编码器可以是一个LSTM网络或者卷积网络;
2、解码器(一个MLP)对该向量进行解码,将其映射为两个参数,分别是:当前时刻多维指标的均值向量和协方差矩阵,这两个参数表征了一个多维高斯分布;
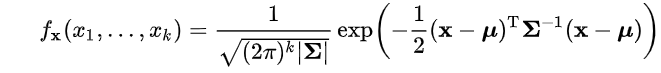
3、概率层摄取高斯分布的参数,计算当前时刻设备状态的概率密度的负对数,通常认为异常状态所对应的概率密度值应远小于正常状态,因此通过为该输出设置阈值,即可用于异常检测;
4、训练过程,只需最小化模型输出即可;
通过输出多维高斯分布的均值向量和协方差矩阵对设备状态的概率密度进行刻画,面临的一个数学问题是,协方差矩阵必须为对称正定矩阵,如果直接通过MLP将语义向量映射为一个方阵,则无法满足对称正定约束,也无法训练。
解决这个问题的方法为cholesky分解,对称正定矩阵总是可以分解为一个对角线元素全为正的上/下三角矩阵及其转置的乘积,反之也成立。
![]()
因此,我们在解码器层,不直接输出协方差矩阵,而是输出precision矩阵(协方差矩阵的逆)的cholesky分解,并保证cholesky分解的对角线元素大于0即可(softplus),进一步可计算得到precision矩阵。
我们仍然使用一个MLP(cov_net)将输入映射为一个方阵,但是只用其上三角部分,并对对角线部分作softplus转换,保证其非负性,作为precision矩阵的cholesky分解。

在概率层,协方差矩阵行列式的计算,可直接使用cholesky分解的对角线乘积的平方即可。

然后,在概率层计算真实数据的负对数似然。

最后模型的优化,只需最小化模型输出即可,通过自定义以下损失函数,训练时将truth设置为0即可达到优化的目的。

与deepar算法的比较:
1、deepar针对单维度时间序列进行建模,本算法针对多维序列进行建模;
2、deepar是一个seq2seq模型,本算法也是encoder-decoder架构,但是只对单点进行建模;
3、deepar输出时间序列的预测值,本算法输出的是数据的负对数似然,即本算法将deepar中概率计算过程从loss拿到了概率层;
4、异常检测方式:deepar使用ancestral sampling重复多次采样,通过计算采样值的上下百分位数作为异常检测的边界,这样的方法存在两个问题:误差累积和计算量大;针对多维数据,无法采用这样的方式,因为多维空间要比一维空间稀疏得多,要想用一系列采样值来表征一个多维分布,样本量必须充分大,这在计算上是不可行的,因此本算法采用单步预测方式,避免了采样带来的问题。
5、deepar向前预测时间序列的未来值,本算法在给定序列值的前提下计算其“合理性”;
6、deepar要求序列未来时刻的协变量是必须是可预知的,本算法无此要求。
以下为将本算法应用于实时电机异常检测的整体过程。
总体流程:
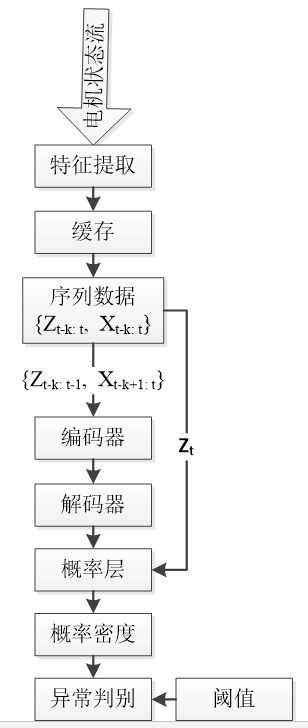
详细过程:
|
原理: 本文提出一种基于编码器、解码器、概率层的三层神经网络结构,对电机的状态进行条件概率建模:
其中,Z代表要建模的目标变量,X代表协变量,下标代表时刻。 主要步骤如下:
原理框图如下,其中各个变量的含义为: X:协变量 Z:目标变量,也即要进行概率建模的变量 t:当前时刻 k:序列长度 Encoded:对序列的编码 miu:高斯分布的均值向量 covariance:高斯分布的协方差矩阵 Gaussian:高斯分布表示的概率层 P:目标变量概率密度的负对数 |
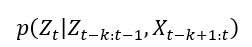


 浙公网安备 33010602011771号
浙公网安备 33010602011771号