NOI 系列赛事

NOI

NOI Online 2020 Round 1

记录+题解

NOI Online 2020 Round 2

记录+题解

NOI 2013

• 向量内积

给定一个 \(n\) 个 \(m\) 维向量，求出一组不同的向量 \(p,q\) 使其内积（点乘）在模 \(k\) 意义下为 \(0\)。

\(k=2,1\le n\le 2\times 10^4, 1\le m\le 100\) 或 \(k=3,1\le n\le 10^5, 1\le m\le 30.\)

*哈希，矩阵，模

神奇套路题。主要思想：随机化哈希判断相等。原理：哈希值相同是真的相同的必要条件。

把向量想象成一个 \(n\times m\) 的矩阵 \(A\)，题目等价于 \(AA^T\) 在非对角线上存在 \(0\) 值。先考虑 \(k=2\) 的情况，只需判断是不是全是 \(1\) 即可。直接做是 \(n^2m\) 的，考虑再乘上一个 \(n\times 1\) 的列向量，可以优化到 \(O(nm)\)。这时只需判断最后的结果是否相同，随几次可以认为是对的。

\(k=3\) 时我们发现 \(1^2\equiv 2^2\equiv 3\pmod 3\)。于是我们把答案的矩阵每个数平方，对应到原来的矩阵即把向量 \(a_1,a_2,...,a_m\to a_1a_1,a_1a_2,...a_1a_m,a_2a_1,a_2a_2,...,a_2a_m,...a_ma_1,a_ma_2,...a_ma_m\)。所以可以 \(O(nm^2)\)。

code

• 矩阵游戏

*数列，费马小定理

先把单独一行拿出来看，设 \(f_1\) 是这一行的第一个元素，有 \(f_i=f_{i-1}*a+b\)。所以 \(f_m=f_1a^{m-1}+\frac{a^{i-1}-1}{a-1}b\)。如果不会的可以再去补一下高中数学。

然后设 \(g_i\) 是第 \(i\) 行的 \(f_m\)，有 \(g_i=(g_{i-1}c+d)a^{m-1}+\frac{a^{i-1}-1}{a-1}b\)，然后换个元又变成上面的式子，搞一搞就出来了。

但是 \(n,m\) 太大怎么搞？我们有一个费马小定理，\(a^{p-1}=1\pmod p,a<p\)。然后就可以降到 \(p\) 以下了。

坑点：注意 \(a=1\) 时等比数列求和公式不存在，需要特判，而次时又需要模 \(p\) 的 \(n,m\)，所以 \(n,m\) 两个都要模。

• 树的计数

*概率期望，树的遍历

首先我们发现我们要求的就是树的期望高度，然后根据期望的线性性我们可以把它分成几层。

观察到这个树的编号是无所谓的，我们可以给bfs序重新编号成 \(1\) 到 \(n\)，同时改变dfs序，这样不会有影响。

又发现bfs是按层来搞的，所以我们下一步就是分层，也就是把bfs划分成几个区间，每个区间在一层。

显然这不可能是随便分层，有一些限制。我们用一个数组来表示 \(i\) 和 \(i+1\) 直接有没有分割，如果为 \(0\) 即为不确定。

1，\(1\) 和 \(2\) 之间一定有分隔。这很显然。

2，假设 \(d_i\) 是 \(i\) 在dfs序中的位置。若 \(d_i>d_{i+1}\) 说明dfs的过程中先遍历到 \(i+1\) 再遍历到 \(i\)，而如果他们在同一层中则不可能（因为是按顺序排的），所以它们一定不在同一层中，答案加一。

3，还有这第三个限制，也是比较难想到的。假设 \(dfn_i\) 是dfs序，若 \(dfn_i+1<dfn_{i+1}\)，说明 \(dfn_{i+1}\) 的 深度最多比 \(dfn{i}\) 多1，所以 \(dfn_{i}\) 与 \(dfn_{i+1}\) 之间最多放一个分隔线，而枚举几种情况发现期间必有一条分隔线，所以这一段不得再有其他分隔线。

最后，如果还是可填可不填的答案就加0.5。

• 快餐店

*基环树，dp

这是一道类似于基环树直径的题。显然答案为直径除以2。

考虑暴力的做法，每次断一条环上边，然后找一下当前的直径，再取一个最小值即可。

优化也很简答，维护四个数组 \(h1,h2,g1,g2\) 分别代表到左端点（环上第一个点）前缀最大值，到右端点（也是环上第一个点（嘿嘿想不到吧，只不过饶了一圈））后缀最大值，以及前缀最大答案和后缀最大答案，不动的看一下图就懂了。

然后我们枚举断边\(i \rightarrow i+1\)，然后拿\(max(h1[i]+h2[i+1],max(g1[i],g2[i+1]))\)来更新答案，别忘了再和不在环上的链取最大。

• 书法家

*dp

从右往左，\(11\) 个 dp。注意细节就好。

NOI 2014

• 购票

数据结构维护区间凸包

应该有一个非常裸的dp：记 \(f_u\) 代表节点 \(u\) 的答案，有 \(f_u=\min_{v\in anc(u),dep_u-dep_v\le l_u}f_v+ (dep_u-dep_v)\times p_u+q_u\) 其中 \(dep_u\) 代表 \(u\) 到根的距离。

然后我们发现如果没有 \(l_u\) 的限制这就是是一个非常套路的斜率优化式，直接套树上斜率优化的板子即可。但是这里有这么一个条件，可是我们发现这个条件其实也是满足一个单调性的，直接二分找到第一个满足这个条件的决策点然后以这个点为决策二分的左端点即可。然后你就可以获得 50 分的好成绩（配合上暴力估计 70 分）。

问题是有可能出现满足条件的点但是不在凸包上，在凸包上的点不满足条件，而这个不在凸包上的点还是最优决策点。

比如说下面这张图：

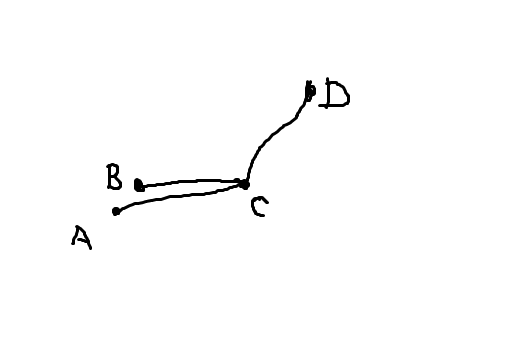
这里 A 不满足条件，但是 B 满足条件且为最优决策点。我们不难发现对于一个决策的可行决策点必然是一段区间，那么我们可以用线段树来维护（线段树上的下标是深度，而线段树所维护的其实是一条从当前点到根的链）。对于线段树上的每一个节点维护这个区间内的决策点所形成的凸壳。因为每个决策点只会在 \(\log{n}\) 的节点内所以总空间复杂度为 \(O(n\log{n})\)，然后对于查询在每个节点上二分找到当前节点的最优再在全部里选一个最优即可，时间复杂度 \(O(\log^2{n})\)，对于插入，每个决策点在 \(\log{n}\) 个线段树上的节点只会插入删除各一次，所以之间复杂度均摊是 \(O(\log{n})\) 的。

不难发现每个查询都是后缀，所以直接树状数组也可（还是线段树写得舒服）。每个节点维护凸壳的方法和树上斜率优化一样，要一个可撤销栈。

点分治

假设当前树的根是 \(x\)，重心是 \(y\)，那么我们考虑用 \(x\rightarrow y\) 这条链上的点用斜率优化更新 \(y\) 的子树内的点。考虑条件 \(dep_{v}-dep_{u}\le l_{v}\)，即 \(dep_{v}-l_{v}\le dep_{u}\)，那么我们把子树内的点按 \(dep_{v}-l_{v}\)，然后链上的点按 \(dep\) 从大到小排序。按顺序加入凸包（尺取）。这时我们就要保证 \(x\rightarrow y\) 的点都算出了其的答案，我们可以先递归处理除了 \(y\) 的子树的部分，这样就得到了实现。

思路很简单写起来恶心得很（注意凸包维护的方向）。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const double inf = 1e18;
const int MAXN = 200005;
int n;
int fa[MAXN];
ll dep[MAXN], lim[MAXN], val[MAXN], p[MAXN], q[MAXN];
vector<int> vec[MAXN];
int stk[MAXN], top;
ll f[MAXN];
ll mini;
int rt;
int sz[MAXN];
bool vis[MAXN]; 
void get_root(int x, int tot_size) {
	sz[x] = 1;
	ll maxi = -inf;
	for (auto y : vec[x]) {
		if (vis[y]) continue;
		get_root(y, tot_size);
		sz[x] += sz[y];
		maxi = max(maxi, (ll)sz[y]);
	}
	maxi = max(maxi, (ll)(tot_size - sz[x]));
	if ((mini > maxi) || (mini == maxi && dep[rt] > dep[x])) {
		mini = maxi;
		rt = x;
	}
}
double X(int i) {
	return dep[i];
}
double Y(int i) {
	return f[i];
}
double slope(int i, int j) {
	if (X(i) == X(j)) return Y(j) >= Y(i) ? inf : -inf;
	return (Y(j) - Y(i)) / (X(j) - X(i));
}
void dfs1(int x) {
	for (auto y : vec[x]) {
		dep[y] = dep[x] + val[y];
		dfs1(y);
	}
}
struct Pair{
	ll val, id;
	friend bool operator < (Pair a, Pair b) {
		return a.val > b.val;
	}
}P[MAXN];
int num;
void dfs(int x) {
	P[++num] = Pair{dep[x] - lim[x], x};
	for (auto y : vec[x]) {
		if (vis[y]) continue;
		dfs(y);
	}
}
void solve(int x, int size) {//处理根为 x，大小为 size 的子树 
	if (size == 1) return;//如果只有一个点直接返回就好了  
	mini = inf;
	get_root(x, size);//找到重心 rt 
	if (mini >= inf) return;
	int RT = rt;//因为 root 有可能更改所以存一下 
	for (auto y : vec[RT]) vis[y] = 1;//把 rt 的子树都打上标记，不让其下到 rt 的子树内 
	solve(x, size - sz[RT] + 1);//处理除了 rt 子树的其他部分 
	//此时从 x 到 rt 的链上的点的 dp 值已经处理出来了 
	num = 0;
	for (auto y : vec[RT]) dfs(y);
	sort(P + 1, P + 1 + num);//从大到小排序 
	int j = RT;
	top = 0;
	for (int i = 1; i <= num; i++) {
		while (j != fa[x] && dep[j] >= P[i].val) {//决策点 j 是满足条件的，将决策点 j 加入凸包 
			while (top > 1 && slope(stk[top], stk[top - 1]) <= slope(j, stk[top])) top--;
			stk[++top] = j;
			j = fa[j];
		}
		//对 i 进行决策 
		if (top > 0) {
			int l = 2, r = top, pos = 1;
			while (l <= r) 
			{
				int mid = (l + r) >> 1;
				if (slope(stk[mid], stk[mid - 1]) >= p[P[i].id]) pos = mid, l = mid + 1;
				else r = mid - 1;
			}
			pos = stk[pos];
			f[P[i].id] = min(f[P[i].id], f[pos] + (dep[P[i].id] - dep[pos]) * p[P[i].id] + q[P[i].id]);
		}
	}
	for (auto y : vec[RT]) solve(y, sz[y]);
}
int main() {
	memset(f, 0x3f, sizeof(f));
	f[1] = 0;
	int T;
	scanf("%d%d", &n, &T);
	for (int i = 2; i <= n; i++) {
		scanf("%d%lld%lld%lld%lld", fa + i, val + i, p + i, q + i, lim + i);
		vec[fa[i]].push_back(i);
	}
	dfs1(1);
	solve(1, n);
	for (int i = 2; i <= n; i++) {
		printf("%lld\n", f[i]);
	}
	return 0;
}

NOI 2018

• 归程

NOI的模板题？貌似2018已经有两道模板了啊？

我们现在想要找到一个点集，使得从起点到点集中的每个点一定存在一条路径使得这条路径上的最小边大于水位线。

这就要使得我们从起点找到一条到每个点的路径使得路径上的最小边尽量打。这不就是kruskal重构树能干的事吗？不会的点我.

我们在重构树上倍增，找到一个深度最浅的节点使得其权值大于水位线，则其子树内的叶节点都是可以到的。

剩下的交给步行，我们发现终点是固定的所以步行的最短路是固定的，直接spfa搞出一个最短路再树形dp统计一下就行。

时间复杂度是\(n\log{n}\)级别的。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
const int N = 400010;
const int M = 400010;
template <typename T> void read(T &x) {
	T ff = 1;
	char cch = getchar();
	for (; '0' > cch || cch > '9'; cch = getchar()) if (cch == '-') ff = -1;
	for (x = 0; '0' <= cch && cch <= '9'; cch = getchar()) x = x * 10 + cch - '0';
	x *= ff;
}
struct node{
	int pre, to, val;
}edge[N << 1];
struct EDGE{
	int u, v, l, w;
	friend bool operator < (EDGE x, EDGE y) {
		return x.w > y.w;
	}
}ed[M];
int head[N], tot;
int fa[N], val[N];
int ch[N][2], dp[N], dis[N];
bool vis[N];
int f[N][21];
int T;
int n, m, cnt;
int Q, k, s;
int ans;
priority_queue<pair<int, int> > q;
void add(int u, int v, int l) {
	edge[++tot] = node{head[u], v, l};
	head[u] = tot;
}
void init() {
	tot = 0;
	for (int i = 1; i <= n; i++) head[i] = 0;
}
void dfs(int x) {
	dp[x] = 0x3f3f3f3f;
	if (val[x] >= 0x3f3f3f3f) dp[x] = dis[x];
	for (int i = 1; i <= 20; i++) {
		f[x][i] = f[f[x][i - 1]][i - 1];
	}
	if (ch[x][0]) {
		f[ch[x][0]][0] = x;
		dfs(ch[x][0]);
		dp[x] = min(dp[x], dp[ch[x][0]]);
	}
	if (ch[x][1]) {
		f[ch[x][1]][0] = x;
		dfs(ch[x][1]);
		dp[x] = min(dp[x], dp[ch[x][1]]);
	}
}
int find(int x) {
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int main() {
	read(T);
	while (T--) {
		read(n); read(m);
		init();
		for (int i = 1; i <= m; i++) {
			read(ed[i].u); read(ed[i].v); read(ed[i].l); read(ed[i].w);
			add(ed[i].u, ed[i].v, ed[i].l);
			add(ed[i].v, ed[i].u, ed[i].l);
		}
		for (int i = 1; i <= n; i++) dis[i] = 0x3f3f3f3f, vis[i] = 0;
		dis[1] = 0;
		q.push(make_pair(-dis[1], 1));
		while (!q.empty()) {
			int x = q.top().second;
			q.pop();
			if (vis[x]) continue;
			vis[x] = 1;
			for (int i = head[x]; i; i = edge[i].pre) {
				int y = edge[i].to;
				if (dis[y] > dis[x] + edge[i].val) {
					dis[y] = dis[x] + edge[i].val;
					q.push(make_pair(-dis[y], y));
				}
			}
		}
		int limit = (n << 1) - 1;
		cnt = n;
		for (int i = 1; i <= limit; i++) fa[i] = i;
		sort(ed + 1, ed + 1 + m);
		for (int i = 1; i <= n; i++) val[i] = 0x3f3f3f3f, ch[i][0] = ch[i][1] = 0;
		for (int i = 1; i <= m; i++) {
			int x = ed[i].u, y = ed[i].v;
			int fx = find(x), fy = find(y);
			if (fx != fy) {
				cnt++;
				val[cnt] = ed[i].w;
				fa[fx] = cnt;
				fa[fy] = cnt;
				ch[cnt][0] = fx;
				ch[cnt][1] = fy;
				if (cnt >= limit) break;
			}
		}
		f[cnt][0] = 0;
		dfs(cnt);
		read(Q); read(k); read(s);
		ans = 0;
		for (int t = 1; t <= Q; t++) {
			int v, p;
			read(v); read(p);
			v = (v + k * ans - 1) % n + 1;
			p = (p + k * ans) % (s + 1);
			for (int i = 20; i >= 0; i--) {
				if (val[f[v][i]] > p) v = f[v][i];
			}
			printf("%d\n", ans = dp[v]);
		}
	}
	return 0;
}

• 屠龙勇士

这道题可谓是大毒瘤了，还要根据数据类型不同测试点不同的方法。

链接

我刚开始看这道题时以为一把剑杀不死龙还可以再换一把继续杀，于是怎么也做不出，后来看看题解发现并不是这样。

是我自己没看清楚题，题目说：“每次面对巨龙时，玩家只能选择一把剑”。

然后思路就很清晰了，先预处理出杀死每一条龙要用的剑的攻击力，设其为 \(ATK\)，设第 \(i\) 条龙的生命值为 \(h_i\)。

题目的要求即为\(h_i \equiv ATKx(\mod p_i)\)的最小正整数 \(x\)。

然而我们会发现一些问题：

如果\(h_i \le p_i\)那这么写没问题，而如果\(h_i > p_i\)则有可能减不到负数就满足要求了。

而我们观察数据可得这种情况（即没有特殊性质1）时都是\(p=1\)，所以特判一下即可。

接着直接套excrt。

Q 如何转换为中国剩余定理的标准形式：\(x \equiv a (\mod b)\)

A 通过exgcd解同余方程。

设当前同余方程为\(ax\equiv b(\mod m)\)，要变成标准形式。

先得到通解（如果得不到则无解）：\(x=x0+k\frac{m}{gcd(a,m)}, k \in Z\)。

两遍同时mod\(\frac{m}{gcd(a,m)}\)得\(x \equiv x0 (\mod \frac{m}{gcd(a,m)})\)

然后就可以愉快地套excrt了。

需要注意的一些东西：

1. 如何求出每次用哪把剑——用一个multiset维护，每次找upperbound（注意这里剑的攻击力是可重的）。

2. 如果\(p_i | ATK\)，则需满足\(p_i | h_i\)否则方程无解。而如果满足则这个方程算是一个废的方程，丢掉即可。

附上我调了一个下午的代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
namespace IO{
	template <typename T> void read(T &x) {
		T f = 1;
		char ch = getchar();
		for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
		for (x = 0; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
		x *= f;
	}
	template <typename T> void write(T x) {
		if (x > 9) write(x / 10);
		putchar(x % 10 + '0');
	}
	template <typename T> void print(T x) {
		if (x < 0) x = -x, putchar('-');
		write(x);
		putchar('\n');
	}
} using namespace IO;
int T;//测试组数 
int n, m;//龙的数量、开始时剑的数量 
ll h[N], p[N], a[N], b[N];//龙的血量、龙每次回复的血量、每次打完龙得到的剑的攻击力、开始m把剑的攻击力 
ll ATK[N];//杀第i条龙用的剑的攻击力 
multiset<ll> s;
ll nn, A[N], B[N];//excrt时方程的数量、值、模数 
void init() {
	s.clear();
	for (int i = 1; i <= m; i++) s.insert(b[i]);//将剑放入set中 
	for (int i = 1; i <= n; i++) {
		set<ll>::iterator it = s.upper_bound(h[i]);
		if (it == s.begin()) ATK[i] = *it;
		else ATK[i] = *--it;
		s.erase(it);//注意这里是迭代器，否则会把所有值为ATK的都删掉 
		s.insert(a[i]);
	}
}
void solve1() {
	//如果全部p为1，则只需取 max{ceil(h[i]/ATK[i])} 即可 
	ll ans = 0;
	for (int i = 1; i <= n; i++) {
		ans = max(ans, (ll)ceil(1.0 * h[i] / ATK[i]));
	}
	print(ans);
}
ll exgcd(ll u, ll v, ll &x, ll &y) {
	if (v == 0) {
		x = 1, y = 0;
		return u;
	}
	ll g = exgcd(v, u % v, y, x);
	y = y - u / v * x;
	return g;
}
ll Mul(ll x, ll y, ll P) {
	return (__int128)x * y % P;
}
bool init2() {
	nn = 0;
	for (int i = 1; i <= n; i++) {
		if (ATK[i] % p[i] == 0 && h[i] % p[i] == 0) continue;
		else if (ATK[i] % p[i] == 0 && h[i] % p[i] != 0) return false;
		else {
			ATK[i] %= p[i];
			ll tmp, tmp2;
			ll g = exgcd(ATK[i], p[i], tmp, tmp2);
			if (h[i] % g) return false;
			nn++;
			B[nn] = (p[i] / g);
			A[nn] = Mul(tmp, (h[i] / g), B[nn]);
			A[nn] = (A[nn] % B[nn] + B[nn]) % B[nn];
		}
	}
	return true;
}

ll solve2() {
	//第二种情况，套excrt 
	if (!init2()) return -1;
	ll X = A[1], M = B[1];
	for (int i = 2; i <= nn; i++) {
		ll z = (A[i] - X);
		z = (z % B[i] + B[i]) % B[i];
		ll t0, tmp;
		ll g = exgcd(M, B[i], t0, tmp);
		if (z % g) return -1;
		t0 = Mul(t0, z / g, B[i] / g);
		t0 = (t0 % (B[i] / g) + B[i] / g) % (B[i] / g);
		X = X + M * t0;
		M = M * (B[i] / g);
	}
	X = (X % M + M) % M;
	return X; 
}
int main() {
//	freopen("dragon.in", "r", stdin);
//	freopen("dragon.out", "w", stdout);
	read(T);
	while (T--) {
		read(n); read(m);
		for (int i = 1; i <= n; i++) read(h[i]);
		for (int i = 1; i <= n; i++) read(p[i]);
		for (int i = 1; i <= n; i++) read(a[i]);
		for (int i = 1; i <= m; i++) read(b[i]);
		init();
		bool flag = 1;
		for (int i = 1; i <= n; i++) if (p[i] != 1) {flag = 0; break;}//特判性质1，稍微压了压行 
		if (flag) {
			solve1();
		} else {
			print(solve2());
		}
	}
	return 0;
}

NOI 2020

• 美食家

老经典题了，先写出一个 dp，\(f[i,j]\) 代表第 \(i\) 天在 \(j\) 号点的最大权值。转移显然，由于 \(w\le 5\) 所以只需保留前 \(5\) 天的值。于是可以构造一个 \(5n\times 5n\) 的矩阵。显然转移这是一个广义矩阵乘法。倍增预处理然后向量\(\times\)矩阵。复杂度 \(O((5n)^3\log T+(5n)^2k\log T)\)。

• 制作菜品

结论就是，如果 \(m\ge n\) 一定有解，否则分成一个森林，使得每个树都满足 \(\sum\limits_{i\in S}d_i =(|S|-1)k\)。

这个结论其实归纳很好瞪，下面来尝试证明（摘抄）：

对于 \(m=n-1\) 的情况，不妨设 \(d_1\le d_2\le \dots\le d_k\)。这时一定有 \(d_1<k\)，且 \(d_1+d_n\ge k\)。那么归纳去把 \(1,n\) 凑一组即可使 \(n=n-1\)。

接下来考虑 \(m\ge n\) 的情况，显然有 \(d_n>k\)，于是用 \(n\) 来做菜就可以使得 \(m=m-1\) 了。

森林的结论就更容易归纳证明了。

至于这道题，我们显然可以 \(O(n^2k)\) 的背包，可以bitset优化。

NOI 2021

• T1 edge

转换题意，操作 1 相当于给每个点染一个新颜色，然后操作 2 相当于数有多少个点与其父亲的颜色相同。于是 \(ans=dis(a,b)-num+1\)，\(num\) 是相同的颜色段数。然后树剖+线段树维护即可。

code

• T2 xpath

看到这个要求的东西换一下元可以发现就是逆序对数，然后偶加奇减这不就是行列式吗？

于是 A 性质就做完了。我们仔细考虑一下这个能不能扩展，其实可以的。我们直接把所有矩阵乘起来然后再求行列式就行了。

这玩意具体有个名字叫 LGV 引理。

code

• T3 celebration

根据题目的性质这玩意缩点之后一定是一颗外向树，于是我们只需要把那 \(k\) 对点拿出来建虚树即可。

草了还是写具体一点吧。

这2k个点中的一个点 u，如果s可以到u或u可以到t，我们把这样的u拿出来，还有s，t。再对于另一个点x，如果有一个那样的点可以到x，x还可以到那样的点，那么x显然就是满足条件的点。

code

• T1

抽屉原理，把串分成 16 段，必有一段完全相同，我们只需找这一段完全相同的即可。

• T2

容易发现最后输出的东西其实是个序列递推，所以我们用平衡树维护矩阵即可。

• T3

不会

NOI 2022

• D1T1 众数

这个定义就很提示在线段树上二分。于是直接线段树维护每个值出现了几次，合并时使用线段树合并。查询的时候分成两个区间，如果某个区间出现次数和大于一半就递归进去，否则一定无解。复杂度 \(O(n\log n)\)。序列合并的时候可以使用链表。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+5;
template<typename T>
void read(T &x){
	T sgn=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar())if(ch=='-')sgn=-1;
	for(x=0;isdigit(ch);ch=getchar())x=x*10+ch-'0';
	x*=sgn;
}
struct node{
	int ls,rs,sum;
}tr[maxn*60];
int n,q,rt[maxn];
int hd[maxn],tl[maxn];
int tot,val[maxn],pre[maxn];
int now[maxn];
int zz;
void modify(int &p,int l,int r,int pos,int v){
	if(!p)p=++zz;
	if(l==r)return tr[p].sum+=v,void();
	int mid=(l+r)>>1;
	if(pos<=mid)modify(tr[p].ls,l,mid,pos,v);
	else modify(tr[p].rs,mid+1,r,pos,v);
	tr[p].sum=tr[tr[p].ls].sum+tr[tr[p].rs].sum;
}
int merge(int x,int y){
	if(!x||!y)return x|y;
	tr[x].sum+=tr[y].sum;
	tr[x].ls=merge(tr[x].ls,tr[y].ls);
	tr[x].rs=merge(tr[x].rs,tr[y].rs);
	return x;
}
int main(){
	read(n);read(q);
	for(int i=1,l;i<=n;i++){
		read(l);
		for(int j=1;j<=l;j++){
			tot++;
			read(val[tot]);
			pre[tot]=tl[i];
			tl[i]=tot;
			if(!hd[i])hd[i]=tot;
			modify(rt[i],1,n+q,val[tot],1);
		}
	}
	for(int t=1;t<=q;t++){
		int op,x,y,z;
		read(op);
		if(op==1){
			read(x);
			tot++;
			read(val[tot]);
			pre[tot]=tl[x];
			tl[x]=tot;
			if(!hd[x])hd[x]=tot;
			modify(rt[x],1,n+q,val[tot],1);
		}else if(op==2){
			read(x);
			modify(rt[x],1,n+q,val[tl[x]],-1);
			tl[x]=pre[tl[x]];
			if(!tl[x])hd[x]=0;
		}else if(op==3){
			read(x);
			ll num=0;
			for(int i=1;i<=x;i++){
				read(y);
				now[i]=rt[y];
				num+=tr[now[i]].sum;
			}
			num>>=1;
			int l=1,r=n+q;
			bool flg=true;
			while(l<r){
				int mid=(l+r)>>1;
				ll curl=0,curr=0;
				for(int i=1;i<=x;i++){
					curl+=tr[tr[now[i]].ls].sum;
					curr+=tr[tr[now[i]].rs].sum;
				}
				if(curl>num){
					for(int i=1;i<=x;i++){
						now[i]=tr[now[i]].ls;
					}
					r=mid;
				}else if(curr>num){
					for(int i=1;i<=x;i++){
						now[i]=tr[now[i]].rs;
					}
					l=mid+1;
				}else{
					flg=false;
					break;
				}
			}
			ll cur=0;
			for(int i=1;i<=x;i++){
				cur+=tr[now[i]].sum;
			}
			if(cur<=num)flg=false;
			if(!flg)puts("-1");
			else printf("%d\n",l);
		}else{
			read(x);read(y);read(z);
			if(!hd[x])hd[z]=hd[y],tl[z]=tl[y];
			else if(!hd[y])hd[z]=hd[x],tl[z]=tl[x];
			else hd[z]=hd[x],tl[z]=tl[y],pre[hd[y]]=tl[x];
			rt[z]=merge(rt[x],rt[y]);
		}
	}
	return 0;
}

• D2T1 挑战 NPC Ⅱ

首先题目最后都提示你需要用到树哈希，那么先默认我们有一个可以O(1)判断树同构的工具。

注意到k很小只有5，所以被删的叶子很少。有一个很显然的贪心是：把两个根的所有儿子树取出来，把哈希值相同的匹配掉。剩下的就是需要删除的。如果这个数很大那么显然不可能。否则直接枚举排列去匹配，多的部分直接整个删掉。毛估估一下这个复杂度不超过O(nk!)。

最后是如何树哈希。反正我来之前是完全忘了这么个玩意的，考场上瞎胡了一个：考虑给所有儿子的哈希值排序然后字符串哈希，最后再随便怼上去一个和深度有关的数。字符串哈希的时候base根据深度随机。

各省省选

十二省联考 2019

联合省选的前身吗？感觉质量还不错，适合当省选，可能不适合训练？

• 异或粽子

有点像一道 JOISC 的题，二分第 \(k\) 大的值是什么，转成了判定+计数问题。从左往右扫描线，维护一棵 01 trie 即可计数。复杂度 \(O(n\log^2 V)\)。

应该还有另一种做法，考虑贪心每次把最大的点对取出来。用一个堆维护，重新求每个右端点最大的匹配左端点，这个可以用可持久化 01 trie 求。复杂度 \(O((n+k)\log V)\)。

傻逼了，可以不可持久化的，变成全局查询即可，纯脑瘫。

注意这两个做法时间复杂度上的区别，两者并无准确的优劣。

• 皮配

先思考 \(k=0\) 时的做法。注意到此时派系和阵营之间没有干扰，所以两个部分可以分别计算。直接背包就可以求出 \(f_i,g_i\) 分别代表蓝阵营人数为 \(i\) 的方案，以及鸭派系人数为 \(i\) 的方案。

结合暴力可以获得 70 pts 的分数。如果暴力只做有限制的部分，即可通过。

GZOI/GSOI 2019

• 与或和

tags：位运算，单调栈；

给定一个 \(N\times N\) 的矩阵，求所有子矩阵的 \(\operatorname{and}\) 和 \(\operatorname{or}\) 的和模 \(10^9+7\)。所有元素 \(\in [0,2^{31}-1]\)，\(1\le N\le 10^3\)。

位运算有一个好处就是可以按位分开考虑，所以我们不妨设每个位置都是 \(0\) 或 \(1\)。

\(\text{and}\) 和：

等价于数有多少个子矩形全是 \(1\)。枚举矩形的底边然后单调栈，反正是个经典问题。复杂度 \(O(N^2)\)。

\(\text{or}\) 和：

统计有多少个矩形包含了至少一个 \(1\)，反面考虑有多少个矩形没有包含 \(1\)，减去即可。使用同样的方法。

总复杂度 \(O(N^2\log V)\)。

code

• GZOI/GSOI2019 逼死强迫症

tags：计数 dp，递推，生成函数，ODE，矩阵快速幂；

用 \(n-1\) 块 \(1\times 2\) 的瓷砖和两块 \(1\times 1\) 的瓷砖铺满 \(2\times n\) 的地板要求两块 \(1\times 1\) 的瓷砖不相邻求方案数。对 \(10^9+7\) 取模。瓷砖可以翻转。\(2\le N\le 2\times 10^9\)。

设 \(f_n\) 代表答案。考虑新增一列，摆 \(1\times 2\) 的瓷砖有两种情况，要不摆一列，要不摆两行两列，贡献为 \(f_{n-1}+f_{n-2}\)。考虑摆 \(1\times 1\) 的瓷砖，发现会多出 \(2\times \sum_{i=1}^{n-2}g_{i-1}\)。也就是枚举另一个 \(1\times 1\) 的瓷砖放在哪？这里又需要求一个 \(g_n\) 代表 \(2\times n\) 的地板用 \(n\) 块 \(1\times 2\) 的瓷砖铺满的方案数。显然有转移 \(g_{n}=g_{n-1}+g_{n-2}\)。容易发现这个 \(g\) 就是斐波那契数列且 \(g_{0}=0,g_{1}=1\)。

然后用 ODE 稍微推一推即可推出通项公式。\(G(x)=\frac{x+1}{1-x-x^2}\)，设 \(h_n=\sum_{i=0}^{n}g_i\)，显然有 \(H(x)=\frac{x+1}{x^3-2x+1}\)。有 \(f_{n}=f_{n-1}+f_{n-2}+2h_{n-3},f_{0}=f_{1}=f_{2}=0\)。于是有

\[F(x)=xF(x)+x^2F(x)+2x^3H(x)\\ F(x)=\dfrac{2x^3H(x)}{1-x-x^2}\\ F(x)=\dfrac{2x^4+2x^3}{(1-x-x^2)(x^3-2x+1)} \]

推出通项貌似有点困难（建议左转oeis.org直接贺），但是不难得出递推式然后矩阵快速幂。

\[F(x)(-x^5-x^4+3x^3+x^2+x+1)=2x^4\\ F(x)=x^5F(x)+x^4F(x)-3x^3F(x)-x^2F(x)+3xF(x)+2x^4+2x^3\\ f_n=3f_{n-1}-f_{n-2}-3f_{n-3}+f_{n-4}+f_{n-5}\\ \]

code

• GZOI/GSOI2019 旅行者

给定一个带权有向图和图上 \(k\) 个点，求两两之间最短路的最小值。

多源最短路。考虑将 \(k\) 个点分成两个部分跑多源最短路，为了使得任意两个点都有机会匹配上可以按二进制下每一位是 \(0\) 还是 \(1\) 来分组。复杂度 \(O(Tm\log^2n)\)。

code

• GZOI/GSOI2019 旧词

先考虑 \(k=1\) 的情况其实就是 LNOI 那道 【LCA】。做法就是扫描线然后把 \(1\to i\) 的路径上的边全部加一，最后统计 \(1\to z\) 的路径上的权值和。考虑这个 \(+1\) 是哪里来的。其实是 \(dep_{u}^1-(dep_{u}-1)^1\)，这题把这个 \(1\) 换成 \(k\) 即可。然后我们也不关心具体的式子把这个值直接算出来即可。然后继续树剖线段树维护即可。时间复杂度 \(O(n\log^2)\)。

子串统计

基本子串结构》

https://www.luogu.com.cn/problem/P8351

给定 \(n\) 个点的树的形态以及点的权值范围 \(k\)，对于任意 \(i\in[1,kn]\)，求有多少种权值分配方案，使得树的最大权独立集大小为 \(i\)。

\(1\le n\le 1000,1\le k\le 5\).

无处存储

虽然说题出的有点唐，但是非要 edu 的话还是不错的。

换一种说法：除了权值和父亲节点两个 \(O(n)\) 数组以外，不能再开 \(O(n)\) 的数组了。考虑分块，理论上随即撒点树分块或者王室联邦分块都可以做这个题。诶好像做完了？怎么这么抽象。具体细节看代码吧。

多边形

算法 1

回忆一下最经典的三角剖分计数是怎么样的？切成两个部分然后递归！也就是说，可以区间 dp。当然这是一个环形的也无所谓，因为可以在结尾再多加一个点，转移的时候枚举中间的断点，但是不能在同一条线上。同时回忆一下普通三角剖分的答案即为卡特兰数。

算法 2

NOIp/CSP

CSP-S 2019

D2T3 树的重心

当年我做这道题时还太嫩了，只能想到暴力。其实如果会了更高的科技这道题只要稍微对暴力优化一下就能 AC（我也不会含泪拼满暴力了）。

废话不说了，暴力的思路就是枚举每一条边然后求两个子树的重心。

直接求重心的复杂度是 \(O(n)\) 的，我们考虑优化到 \(O(\log{n})\)。

我们想要求以 \(x\) 为根的子树的重心，首先有个引理：这个重心一定在以 \(x\) 开头的这条重链上（这里就是轻重链剖分中的重链）。

这其实蛮好理解的，如果 \(x\) 不是重心，则只有其重儿子才有可能是重心，同理只有其重儿子的重儿子才有可能是重心，所以重心一定在重链上。

重心一定有且最多有两个，所以我们在重链上找一个最深的点 \(y\) 使得 \(n-sz[y] \le \frac{n}{2}\)，这个点有可能成为重心。

重心的另一个性质是如果两点是重心则其一定相连。这样我们只需判断 \(y\) 和 \(father[y]\) 是不是中心即可。

怎么找到 \(y\)？我们发现在重链上倍增就行，类似倍增求 lca。

怎么维护众多数组？换根就行。

CSP-S 2022

• 假期计划（holiday）

给定 \(n\) 个点 \(m\) 条边的无向图，点有点权。求出 \(4\) 个不同的点，\(A,B,C,D\)，使得 \(1\to A,A\to B,B\to C,C\to D,D\to 1\) 的最短路均不大于给定的数 \(k\)。求 \(A,B,C,D\) 最大点权和。\(1\le n\le 2500\)。

难度大概在 \(2100\sim 2200\)？先进行 \(n\) 次 bfs，求出任意两点最短路，现在称最短路不大于 \(k\) 的点对有连边。显然路径可以拆成两条 \(1\to x\to y\)，枚举 \(B,C\) 是一个较为明智的选择。将所有 \(1\) 周围的点染色，现在就是要找到两个不同的染色点，且与 \(B,C\) 也不相同，并且和尽量大。对于 \(B,C\) 分别找三个最大的点，这样显然至少有一组满足条件。复杂度 \(O(n^2)\)。

• 策略游戏（game）

给定两个序列 \(a_1,a_2\dots a_n,b_1,b_2,\dots b_m\)，多组询问，每次给定 \(l_1,r_1,l_2,r_2\)，Alice 先选择一个 \(x\in [l_1,r_1]\)，然后 Bob 选择一个 \(y\in [l_2,r_2]\)，最后的得分是 \(a_x\times b_y\)。Alice 要最大化得分，Bob 要最小化得分，求两人足够聪明的情况下最终的得分。\(1\le n,m,q\le 10^5,|a_i|,|b_i|\le 10^{9}\)。

假设 A 选好了 \(x\)，B 会根据 \(a_x\) 的奇偶性选择 \(y\)，如果 \(a_x\ge 0\)，\(B\) 会选择最小的 \(b_y\)，否则会选择最大的。B 的决策固定了，A 自然就有应对方法。具体来说，如果最小的 \(b_y<0\)，那么 A 就不能选一个很大的 \(a\)，他会选择尽量小 \(a_x\ge 0\)。如果 \(b_y\ge 0\)，那么 A 就能选择一个相对较大的数。对于另一个部分同理。使用 \(O(n)-O(1)\) rmq，可以做到线性。

• 星战（Galaxy）

给定 \(n\) 个点 \(m\) 条边的有向图，每条边都有激活和失活两种状态，初始时均为激活状态。四种操作：

1. 失活某条边。
2. 失活以某个点为终点的所有边。
3. 激活某条边。
4. 激活以某个点为终点的所有边。

询问：如果只考虑激活的边，是否满足：所有的点出度均为 \(1\)。

考场上想了巨久怎么根号分治，写了个假的，不会。

考虑一些乱搞。当总边数为 \(n\) 的时候，所有点出度为 \(1\) 等价于所有点出度均为奇数。奇偶性考虑异或（异或偶数次等于 \(0\)）。一个比较理想的情况，第 \(i\) 个点有一个权值 \(2^i\)，然后每有一条 \(i\) 连出去的边，都异或一遍它的权值。对于每个修改都容易 \(O(n)\) 维护。使用 bitset 可以做到 \(O(\frac{n^2}{w})\)。不妨给每个点随机一个权值，错误概率我也不会分析。

还有另一种哈希，是一种求和的，本质类似这里不再赘述。

• 数据传输（transmit）

直接 dp 然后倍增矩阵优化。