数论与代数

前几天在b站上看到一本书 CINTA（a Concrete Introduction to Number Theory and Algebra），感觉内容着实不错，几乎把同余这一块的内容讲完了，本文将会参考这本书，可以当作这本书的一个阅读笔记。

Github

其实这一块的内容并不常考，需要用到的时候通常没有很强的技巧，所以记好模板是很重要的一步。本文并不局限于这一本书，将有更多OI结合的应用。

写于2023年1月30日，深圳罗湖家中。

---

在原书的内容上添加了一部分东西

2.4 类欧几里德算法

2.5 万能欧几里德算法

4.4 扩展欧拉定理

10.2 扩展中国剩余定理

11.5 Cipolla 算法

15.5 Index Calculus 算法

17 连分数

18 二次域

---

1 整数和二进制#

只用 $01$ 来表示所有数值的系统，二进制是计算机的基础。

$b$ 可以用 $2$ 的次幂唯一表达：$b=\sum\limits_{i=0}^{n}b_i2^{i}$。

加法与乘法，这里必须采用位运算。

view code

a+b=(a^b)+(b&a)

定义 带余除法

对于给定的任意整数 $a,b$ 其中 $b>0$，存在唯一的整数对 $q,r$ 使得 $a=bq+r$ 且 $r\in [0,b-1]$。

证明用到良序原则（自然数的非空子集必然存在一个最小元素）。

先考虑存在性的证明。构造集合 $S=\{a-bk|k\in \Z,a-bk\ge 0\}$，那么必然存在一个最小元 $r$，满足 $a-qb=r,a=qb+r$。接下来证明 $r<b$，这很显然，因为如果 $r\ge b$ 则存在 $r'=r-b\ge 0$，也在集合 $S$ 中，矛盾。接下来证明唯一性。由于 $r\ge 0$，所以只存在唯一的 $r$ 满足 $0\le r<b$，那么也就只有唯一 $q$。

定义 整除

若 $a=bq$ 则称 $b$ 整除 $a$，记作 $b\mid a$。称 $b$ 是 $a$ 的约数。整除具有传递性。

定义 最大公约数

对于两个数$a,b$，如果 $d\mid a$ 且 $d\mid b$ 则称其为公约数，其中最大的称为最大公约数记作 $\gcd(a,b)$。

定义 素数 只有 $1$ 和其本身两个约数的数是素数，除了 $1$ 和其本身还有其他的约数的数是合数，$1$ 和 $0$ 既不是素数也不是合数。

定理 唯一分解定理

任意正整数 $n=\prod\limits_{i=1}^{m}p_{i}^{c_i}$，其中 $p_i$ 是质数。

习题#

1.6 任意整数的平方都形如 $3k$ 或者 $3k+1$，$k\in \Z$。

• $n=3q$ 时，$n^2=9q^2$ 满足。
• $n=3q+1$ 时，$n^2=9q^2+6q+1$ 满足。
• $n=3q-1$ 时，$n^2=9q^2-6q+1$ 满足。

1.8 证明 $2^{n}-1,n>2$ 不是完全平方数。

由于 $2^n$ 一定是偶数，所以 $x$ 一定是奇数 $x=2k+1$，所以 $x^2=4(k^2+k)+1$，显然没有解。

2 欧几里德算法及相关定理#

2.1 欧几里德算法#

定理 欧几里德算法

$\gcd(a,b)=\gcd(b,a\bmod b)$。其中 $a\bmod b$ 代表 $a$ 带余除法 $b$ 所得的余数 $r$。

证明之前先证一个引理，$\gcd(a,b)=\gcd(b,a-b)$。假设 $\gcd(a,b)=d$，设 $a=ud,b=vd,\gcd(u,v)=1$，那么 $a-b=d(u-v)$。所以 $\gcd(b,a-b)=d\gcd(v,u-v)=d$。这里用反证法，如果 $\gcd(v,u-v)=k>1$，那么设 $v=kx,(u-v)=ky$ 则 $u=k(x+y)$，那么 $\gcd(u,v)$ 至少是 $k$。这和 $\gcd(u,v)=1$ 矛盾。

有了这个引理之后，根据带余除法的定义，就可以证明该定理了。

view code

int gcd(a,b) { return b == 0 ? a : gcd(b, a % b); }

命题 对任意两个正整数 $a$ 和 $b$，有 $\gcd(2^{a−1},2^{b−1})=2^{\gcd(a,b)}−1$。

扩展一下，变成 $\gcd(x^{a}-1,x^{b}-1)=x^{\gcd(a,b)}−1$。

不妨设 $a\ge b$，那么 $x^{a}-1-(x^{b}-1)=x^{b}(x^{a-b}-1)=k(x^{r}-1)$。故 $\gcd(x^{a}-1,x^{b}-1)=\gcd(x^{b}-1,x^b(x^{a-b}-1))$。又因为相邻两个数互质，所以 $\gcd(x^b-1,x^b(x^{a-b}-1))=\gcd(x^b-1,x^{a-b}-1)$。所以有了 $\gcd(x^a-1,x^b-1)=\gcd(x^b-1,x^{a\bmod b}-1)$。

终止的条件即为 $b\mid a$，这时即为 $x^{\gcd(a,b)-1}$。

定理 欧几里德算法的时间复杂度是 $O(\log \max(a,b))$。

只需证明，$a\ge b,a\bmod b<\frac{a}{2}$。分类讨论即可。

2.2 Stein 算法#

又称作二进制欧几里德算法。

• 如果 $2\mid a,2\mid b$，则 $\gcd(a,b)=2\gcd(a/2,b/2)$。
• 如果 $2\mid a,2\nmid b$，则 $\gcd(a,b)=\gcd(a/2,b)$。
• 如果 $2\nmid a,2\mid b$，则 $\gcd(a,b)=\gcd(a,b/2)$。
• 如果 $2\nmid a,2\nmid b$，则 $\gcd(a,b)=\gcd(a-b,b)$。

这个算法中没有乘法和除法以及取模运算，只用到了位运算，效率得到了提升。

然而实现表明这个算法是最慢的，因为它的理论常数会是最大的。即欧几里得算法准确复杂度应该是 $\Theta(\log (\frac{\max(a,b)}{\gcd(a,b)}))$

2.3 扩展欧几里德算法#

定理 裴蜀定理 方程 $ax+by=\gcd(a,b)$ 存在整数解 $x=s,y=t$。

纯数学证明可以构造集合并继续应用良序定理，这里给出扩展欧几里德算法的直接构造。

设 $\gcd(a,b)=d$，欧几里得算法的最后一步会得到两个数 $d, 0$，然后令$s=1,t=0$，就得到了一组解$d+0=d$。假设当前我们要求一组解满足 $ax+by=d$，且我们已经得到了一组解满足 $bs+(a\bmod b)t=d$。拆开来得到 $at+b(s-\lfloor\frac{a}{b}\rfloor t)=d$，所以我们可以令$s'=t, t'=s-\lfloor\frac{a}{b}\rfloor b t$ 而得到一组解$s',t'$。一直这么推下去就可以得到最后的答案。

其实这是一个高斯消元的过程。

同样我们有二进制版本的扩展欧几里得算法。区别在于 $a$ 是偶数的时候用 $x'=x\frac{b+1}{2}$ 而不是直接 $x'=x/2$。

Luogu5656 【模板】二元一次不定方程 (exgcd)

求解二元一次不定方程 $ax+by=c$。

题解

2.4 类欧几里德算法#

看这里

2.5 万能欧几里德算法#

习题#

更多命题的证明在习题

2.5 将裴蜀定理扩展到 $n$ 元。

首先证明 $\gcd(a_1,a_2,\dots,a_n)=\gcd(\gcd(a_1,a_2,\dots,a_{n-1}),a_{n})$。这个好像比较显然，那么就可以归纳证明了。

2.6 假设 $g^a \equiv 1\pmod m$ 且 $g^b\equiv 1\pmod m$，请证明 $g^{\gcd(a,b)}\equiv 1\pmod m$。

用之前的证明的命题，$g^{\gcd(a,b)}-1=\gcd(g^{a}-1,g^{b}-1)$，由于 $m\mid g^{a}-1,m\mid g^{b}-1$，所以 $m\mid \gcd(g^{a}-1,g^{b}-1)=g^{\gcd(a,b)-1}$。

2.7 对任意不同的正整数 $m$ 和 $n$，$F_m$ 与 $F_n$ 互素。其中 $F$ 是费马数。

不妨设 $m\ge n$，$F_{m}=2^{2^{m}}-1+2$，$2^{2^n}+1\mid 2^{2^{n+1}}-1\mid 2^{2^{m}}$。于是有 $F_m\equiv 2\pmod F_n$，又 $2\nmid F_n$，所以 $\gcd(F_m,F_n)=1$。

2.12 证明：对任意整数 $a,b,d$，$\gcd(a^d,b^d)=\gcd(a,b)^d$。

设 $k=\gcd(a,b),a=ku,b=kv$，则 $\gcd(k^du^d,k^dv^d)=k^d\gcd(u^d,v^d)=k^d$。

2.14 证明：对任意整数 $n,2n+1,9n+4$ 互素。

构造裴蜀定理 $(-2)n+2n+1=1$。同理 $9(2n+1)-2(9n+4)=1$。

2.16 对非零整数 $a$ 和 $b$，如果整数 $m$ 满足：$a\mid m$ 且 $b\mid m$，则称 $m$ 为 $a$ 和 $b$ 的公倍数，称最小的 $m$ 为最小公倍数，记作 $\mathrm{lcm}(a,b)$。证明 $\mathrm{lcm}(a,b)=\frac{ab}{\gcd(a,b)}$。

设 $d=\gcd(a,b)$，则 $a=dm,b=dn$，则最小公倍数得是 $m,n,d$ 的倍数又 $(m,n)=1$ 所以$\mathrm{lcm}(a,b)=dmn$。

最大公约数和最小公倍数的唯一分解定理

若 $a=\prod p_i^{c_i},b=\prod p_i^{d_i}$，则 $\gcd(a,b)=\prod p_i^{\min(a,b)},\mathrm{lcm}(a,b)=\prod p_i^{\max(a,b)}$。

CF510D Fox And Jumping

根据裴蜀定理，$ax+by$ 能表示出所有数当且仅当 $(a,b)=1$。所以这变成了一个背包问题，设 $dp_i$ 代表选出的数的最大公约数为 $i$ 的最小价值。最后的答案为 $dp_1$。

我们可以通过 $dp_j$ 来更新 $dp_{\gcd(j,c[i])}$。但 $\gcd$ 可能很大，不能直接枚举。所以我们可以用平衡树把所有已经可能出现的 $\gcd$ 存下来，然后用其来更新。

3 同余与模运算#

3.1 同余与模算术运算#

定义 同余

如果整数 $a,b$ 和 $m$ 满足 $m\mid (a-b)$，则称 $a,b$ 模 $m$ 同余。记作 $a\equiv b\pmod m$。

命题 如果 $a_1\equiv b_1\pmod m$ 而且 $a_2\equiv b_2\pmod m$，则 $a_1\pm a_2\equiv b1\pm b2 \pmod m$ 且 $a_1a_2\equiv b_1b_2 \pmod m$。

定理 消去律

设 $a,b,c\in \Z$，$m$ 是一个正整数。如果 $\gcd(c,m)=1$，且 $ac\equiv bc \pmod m$，则 $a\equiv b \pmod m$。

$m\mid (ac-bc)=c(a-b)$，由于 $\gcd(c,m)=1$ 所以 $m\mid a-b$。

定义 乘法逆元

$a^{-1}$ 满足 $aa^{-1}\equiv 1\pmod m$。显然乘法逆元不一定存在。

NOIP2012 同余方程

求关于 $x$ 的同余方程 $ax\equiv 1\pmod b$ 的最小正整数解。

也就是 $ax+by=1$ 的最小正整数解，运用扩展欧几里德算法即可。

求 $1,2\cdots,n$ 模 $p$ 的逆元。

设 $p=ki+j, 0 \le j < i$。

$$ki+j \equiv 0 \pmod p\\ (ki+j)i^{-1}j^{-1} \equiv 0 \pmod p\\ kj^{-1}+i^{-1} \equiv 0 \pmod p\\ i^{-1} \equiv -kj^{-1} \pmod p\\ i^{-1} \equiv (p-[p/i]) \times (p \mod i)^{-1} \pmod p\\ $$

定义 等价类

显然，同余关系是一种等价关系。如果有一种等价关系定义在集合 $S$ 上，则该等价关系会把集合 $S$ 划分为不相交的子
集，这些子集我们称为等价类。

定义 同余类

考虑整数集合 $\Z$，设 $m$ 为正整数，则模 $m$ 的同余关系把 $\Z$ 划分为 $m$ 个等价类。任意整数 $a$ 所落在的等价类记为 $[a]_m$，即所有模 $m$ 同余的整数形成的集合。

模 $m$ 同余类的集合记为 $\Z/m\Z$，该集合恰好有 $m$ 个元素，即：$\Z/m\Z={[0]_m,[1]_m,\dots,[m − 1]_m}$。

定义 最小剩余系

$\Z/m\Z$ 的所有最小非负代表元的集合 $\{0,1,2,\dots,m-1\}$。

3.2 二进制补码#

考虑 $1\le x\le 2^{n-1}-1$，那么对于负数 $-x$，我们找到他其实就相当于找到一个 $x+x'\equiv 0\pmod 2^{n}$，而这个值就应该是 $2^{n}-x$。取反加一的操作，其实就相当于变成了 $2^{n}-x$。

3.3 模指数运算#

定理 快速幂

$a^b\equiv a^{\sum_{i=0}^{n}b_i2^{i}}\pmod m$，于是就可以在 $O(\log b)$ 的时间求出 $a^{2^{i}}$ 和 $a^{b}$。

Luogu1593 因子和

我们知道对于一个整数 $n$，可以分解成 $p1^{c1} \times p2^{c2} \times \cdots \times pm^{cm}$。其因子和应为 $\Pi_{i=1}^{m}\sum_{j=0}^{c_i}p^{j}$。

答案为 $\Pi_{i=1}^{m}\sum_{j=0}^{{c_i}^{b}}p^{j}$。我们发现 $\sum$ 里面即为等比数列求和。直接套公式为$s=\frac{p^{{c_i}^b+1}-1}{p-1}$。

习题#

3.4 给定整数 $p$ 和 $N$，且 $p\mid N$。证明：对任意整数 $x$，$(x \bmod N) \mod p=x \bmod p$。

使用剩余系即可证明。

3.11 证明 $ac\equiv bc\pmod m$，$\gcd(c,m)=d$，则 $a\equiv b\pmod{\frac{m}{d}}$。

用 3.4 的结论即可说明。

4 费马小定理和欧拉定理#

4.1 费马小定理#

引理 $a\times i\bmod p,1\le a<i$ 是 $1,2,\dots,p-1$ 的一个置换。

反证法，若存在 $ai\equiv aj\pmod p$，则 $i\equiv j\pmod p$ 矛盾。

定理 费马小定理

$a^{p-1}\equiv 1\pmod p$。

$$\prod_{i=1}^{p-1}i\equiv \prod_{i=1}^{p-1}ai=a^{p-1}\prod{i=1}^{p-1}i\pmod p$$

所以显然有 $a^{p-1}\equiv 1\pmod p$。

4.2 欧拉函数#

记 $1,2,\dots, n$ 中与 $n$ 互质的数的个数为 $\varphi(n)$，即为欧拉函数。

命题 若 $p$ 是素数，$\varphi(p)=p-1,\varphi(p^c)=p^{c-1}(p-1)$。

显然 $p$ 的剩余系里都与 $p$ 互质，那么每 $p$ 个数里会有 $p-1$ 个互质，于是 $\varphi(p^c)=p^c\frac{p-1}{p}$。

定理 欧拉函数是积性函数，即 $\gcd(a,b)=1\Rightarrow \varphi(ab)=\varphi(a)\varphi(b)$。

这其实可以用剩余系得思想来推，即证明 $\Z/a\Z\times \Z/b\Z$ 双射 $\Z/ab\Z$。当然还可以用容斥的角度，类似上面的证明。还有一个比较巧妙的用了狄利克雷卷积，这里就不过论述。

命题 $\sum\limits_{d|n} \varphi(d) = n$

$\{1,2,\dots,n\}=\cup_{d\mid n}\{x\in [1,n]\cap \Z\|\gcd(x,n)=d\}$，而后者刚好就是 $\varphi(\frac{n}{d})$。

欧拉函数的应用

4.3 欧拉定理#

定理 欧拉定理

$a^{\varphi(m)}\equiv 1\pmod m,\gcd(a,m)=1$。

定义 简化剩余系

所有和 $m$ 互质的数构成的剩余类的集合。

证明欧拉定理等价于证明简化剩余系 $\times a$ 是简化剩余系的置换，其实和上面的反证法一模一样。

4.4 扩展欧拉定理#

定理 扩展欧拉定理

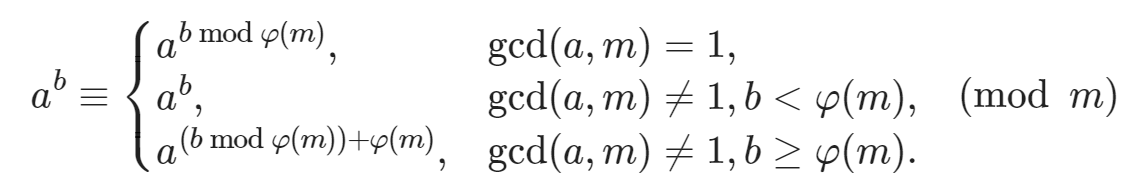
好复杂，但是可以根据欧拉定理记忆，先丢一个证明。

习题#

六省联考2017 相逢是问候

给定 $n,m,p,c$ 区间操作将每个数变成 $c^{a_i}$，区间求和 $\bmod p$。

CF906D Power Tower

给定一个数列 $w$ 和模数 $p$,每次询问一个区间 $[l,r]$,求 $w_{l}^{w_{l+1}^{w_{l+2}^{...}}} \bmod p$ 的值。

这两个题的思路是类似的，就是运用 $p=\varphi(p)$ 这个迭代过程是 $O(\log p)$ 次的这个结论，进行暴力迭代。

5 素数与素性测试#

5.1 素数#

本章重点介绍素数的性质。

定理 素数的整除性

设 $a,b\in \Z$，$p$ 为素数。如果 $p\mid ab$，则 $p\mid a$ 或 $p\mid b$。

推论，$n>0,n\mid ab,\gcd(n,a)=1\Rightarrow n\mid b$。

定理 欧几里得定理

素数有无穷多。

使用反证法。设素数有穷，$p_1,p_2,\dots p_{n}$，构造 $N=1+\prod\limits_{i=1}^{n}p_i$，这个数显然不能被任意一个素数整除，那么也就不能被任意一个数整除，所以它也是一个素数。

定理 狄利克雷定理

存在无穷多的素数满足 $p\equiv a\pmod m$，其中 $\gcd(a,m)=1$。

定理 素数定理

记 $\pi(x)$ 为素数个数，则 $\lim\limits_{x\to \infty}\frac{\pi(x)}{x/\ln x}=1$

威尔逊定理

$p$ 是素数的充要条件是 $(p-1)! \equiv -1 \pmod p$

$p=1$ 时显然不行。

先证充分性，对于$2\le a<b\le p-2$ 有 $a^{-1}\ne b^{-1}$，我们只需将$a\in[2,p-2]$ 与 $a^{-1}$ 配对即可，充分性得证。

必要性显然，若 $p$ 为合数则取一个质因子即可。

5.2 素性测试#

本节讨论素性测试问题，即如何判断一个大的奇整数 n 是否素数。

5.2.1 试除法#

枚举 $2\sim n-1$，看看能不能整除 $n$。这是最暴力的方法，时间复杂度$O(n)$

对上述算法优化，约数是成对出现的所以枚举到 $\sqrt{n}$ 即可，时间复杂度 $O(\sqrt{n})$。

5.2.2 Miller-Rabin 素性测试#

费马小定理的逆定理虽然不成立，但是可以勉强用来判断。而满足费马小定理的合数称作卡麦尔数。

定理 二次探测定理

如果 $p$ 为质数，则 $x^2 \equiv 1 \mod p$ 且 $x \in [1, p-1]$ 的解为 $x=1,p-1$。

我们可以在费马小定理后以此判断 $a^{(p-1)/2},a^{(p-1)/4}$ 是不是 $1/-1$。

已经证明若随机选择 $k$ 个底数则这样做出现伪素数的概率不大于 $\frac{1}{4^k}$。

code

习题#

6 群与子群#

定义 群

对于一个集合 $S$ 和一个二元运算 $*$，如果其满足：

• 封闭性：$\forall a,b\in S, a*b\in S$。
• 结合律：$a*(b*c)=(a*b)*c$。
• 存在单位元 $e$，使得 $\forall a\in S,a*e=e*a=a$。
• 存在逆元，使得 $\forall a\in S, \exist b\in S,a*b=e$。、

定义 阿贝尔群

如果群 $G$ 满足 $\forall a,b\in G,a*b=b*a$ 则称 $G$ 是交换群或阿贝尔群。

6.1 显然乘法逆元在 $\mathbb{Z}$ 不封闭，而在 $\mathbb{Q,R}$ 内封闭。

6.2 没啥好解释的。

6.3 $0$ 不存在乘法逆元。

6.4 根据费马小定理的证明可知。

6.5 根据欧拉定理的证明可知。

6.6 显然矩阵乘法不满足交换律

6.7 $n$ 阶置换群，单位元是 $(1,2,\dots,n)$。

6.8 即对于 $a^2+b^2=1,c^2+d^2=1,(ac-bd)^2+(ad+bc)^2=1$，这是显然的。

6.2 群的基本性质#

命题 6.1 群的单位元唯一

如果存在两个不同的单位元 $e,e'\in\mathbb G$，则有 $ee'=e=e'$，矛盾。

命题 6.2 逆元唯一

若存在 $m,n$，使得 $gm=gn=e$，则 $n=ne=ngm=em=m$。

命题 6.3 设 $\mathbb G$ 为群，任取 $a,b\in\mathbb G$，则 $(ab)^{-1}=b^{-1}a^{−1}$。

由逆元唯一和 $b^{-1}a^{−1}$ 满足逆元定义可得。

命题 6.4 设 $\mathbb G$ 是一个群，对所有群元 $g\in\mathbb G,(g^{−1})^{−1}=g$。

将 $g^{-1}$ 带入 $gg^{-1}=e$ 得 $g^{-1}(g^{-1})^{-1}=e$，$(g^{-1})^{-1}=e(g^{-1})^{-1}=gg^{-1}(g^{-1})^{-1}=ge=g$ 所以命题成立。

对于群来说消去律一定存在。

定义 单射、满射和双射

给定映射 $\phi : A \mapsto B$，如果对任意 $\phi(x_1)=\phi (x_2)$，则有 $x_1=x_2$，则称映射 $\phi$ 为单射（Injection），也称为一一映射。如果对任意 $y\in B$，都存在 $x\in A$，使得 $\phi(x)=y$，则称映射 $\phi$ 为满射（Surjection）。如果映射 $\phi$ 同时满足单射性和满射性，则称映射 $\phi$ 为双射（Bijection）。

定义 置换群

定义映射 $\lambda_a : g\mapsto ag$，显然映射后还是群 $G$。容易发现这种映射是双射。所有映射组成一个群 $\mathbb{G'}$ 称为置换群。

设 $\mathbb{G}$ 是一个群且 $g\in \mathbb{G}$，则 $g^{n}$ 代表进行 $n$ 次群运算后的结果。

由于群的计算是有结合律的所以 $g^mg^n=g^{m+n}$，$(g^{m})^{n}=g^{mn}$，$(gh)^n=(h^{-1}g^{-1})^{-n}$。

定义 阶（order）

有限群的阶定义为群的大小，无限群的阶定义为无穷大。对于群内的一个元素 $g\in \mathbb{G}$，有 $g^m=e$，则称最小的 $m$ 为 $g$ 的阶写作 $\mathrm {ord(}g)$，假设不存在则该群是无限群。

6.3 子群#

若 $\mathbb G$ 为群，$\mathbb H\subseteq \mathbb G$ 且 $\mathbb H$ 在群 $\mathbb G$ 的操作上也满足群公理，则称 $\mathbb H$ 是 $\mathbb G$ 的子群，记作 $\mathbb H\le\mathbb G$。

子群判定定理

群 $\mathbb G$ 的非空子集 $\mathbb H$ 是 $\mathbb G$ 的子群，当且仅当 $\mathbb H$ 同时满足以下条件：

• 若 $a,b\in \mathbb H$，则 $ab\in \mathbb H$；
• 若 $a\in \mathbb H$，则 $a^{−1}\in \mathbb H$。

已知 $a,a^{-1}$ 均在群内，则 $aa^{-1}=e$ 在群内，证毕。

群 $\mathbb G$ 的非空子集 $\mathbb H$ 是 $\mathbb G$ 的子群，当且仅当对任意 $a,b\in \mathbb H，ab^{−1}\in \mathbb H$。

$aa^{-1}=e\in \mathbb H$。

有限群 $\mathbb G$ 的非空子集 $\mathbb H$ 是 $\mathbb G$ 的子群，当且仅当 $\mathbb H$ 中的元素在群 $\mathbb G$ 的操作下满足封闭性。

在之前的引理下只用证明 $a\in \mathbb H\Rightarrow a^{-1}\in \mathbb H$。

由于 $H$ 封闭且有限，所以构造序列 $a,a^2,a^3,\dots$ 一定存在两个数 $a^i=a^j$，则 $a^{i-j}=e,a^{i-j-1}=a^{-1}$。

中心化子

对于任意群元素 $a\in \mathbb G$，定义 $C(a)=\{g\in \mathbb G:ag=ga\}$。集合 $C(a)$ 被称为 $a$ 的中心化子。

中心

$\mathbb Z(\mathbb G)=\{g\in \mathbb G,\forall x\in \mathbb G, gx=xg\}$。

显然 $\mathbb Z(G)=\cap_{a\in \mathbb G}C(a)$

习题#

6.5 证明对任意偶数阶群 $\mathbb G$，都存在 $g\in \mathbb G$，$g\ne e$ 且 $g^2=e$。

显然存在 $g'\in \mathbb G,g'^{|\mathbb G|}=e$，则存在 $g=g'^{\frac{|G|}{2}}$ 满足条件。

6.8 证明：任意群 \mathbb G 的两个子群的交集也是群 $\mathbb G$ 的子群。

对于群 $\mathbb G$ 的两个子群 $\mathbb H_1,\mathbb H_2$，其满足 $a,b\in \mathbb H_1\cap \mathbb H_2$ 都有 $ab\in \mathbb H_1\And ab\in \mathbb H_2\Rightarrow ab\in \mathbb H_1\cap\mathbb H_2$。

6.9 证明或证伪：任意群 $\mathbb G$ 的两个子群的并集也是群 $\mathbb G$ 的子群。

随便举例一个，$2\mathbb{Z}\le \mathbb{Z},3\mathbb{Z}\le \mathbb{Z},2+3=5\notin 2\mathbb{Z}\cup 3\mathbb{Z}$。

6.10 $G$ 是阿贝尔群，$H$ 和 $K$ 是 $G$ 的子群。请证明 $HK=\{hk:h\in H,k\in K\}$ 是群 $G$ 的子群。如果 $G$ 不是阿贝尔群，结论是否依然成立？

6.11 设 $G$ 是阿贝尔群，$m$ 是任意整数，记 $G^m=\{g^m:g\in G\}$。请证明 $G^m$ 是 $G$ 的一个子群。

$g^{m},g^{-m}$ 均在群 $G^m$ 里，

6.12 设 $G$ 是阿贝尔群，$m$ 是任意整数，记 $G[m]=\{g\in G:g^m=e\}$。请证明 $G[m]$ 是 $G$ 的一个子群。

6.13 证明：阿贝尔群 $G$ 中的有限阶元素形成子群。该子群有一个特殊的名字，称为挠子群（Torsion Subgroup）。

6.14 给定一个正整数 $n$（可以是素数也可以是合数），将 $\mathbb{Z}_n^{*}$ 中所有元素相加并模 $n$ 会等于什么？请证明。

会等于 $0$，$s=\sum_{d}d[\gcd(d,n)=1]=\frac{n\varphi(n)}{2}$。在 $n=2$ 时显然成立，在 $n>2$ 时 $\varphi(n)$ 会是偶数。

7 循环群#

7.1 循环群#

设 $\mathbb{G}$ 是群，$\forall g\in \mathbb{G}$，集合 $\langle g\rangle =\{g^x:x\in \mathbb{Z}\}$ 是 $\mathbb{G}$ 的子群。称 $\langle g\rangle$ 为 $g$ 的生成循环群，且这是最小的包含 $g$ 的子群。

循环群的生成元就是阶等于群的阶的元素。

命题 所有的循环群都是阿贝尔群。

设 $\mathbb{G}=\langle g\rangle$ 是循环群，生成元是 $g$，则所有元素 $a,b$ 可表示成 $g^{r},g^s$ 则显然 $ab=g^{r+s}=g^{s+r}=ba$。

命题 循环群 $\mathbb{G}=\langle g\rangle$ 的每一个子群都是循环群。

7.2 原根#

对于群 $\mathbb{Z}_n^{*}$ 是循环群，则称其生成元是 $n$ 的原根。即满足阶是 $\varphi(n)$ 的元素 $g$。

满足 $n=2,4,p^a,2p^a$ 的群 $\mathbb{Z}_n^{*}$ 都是循环群。

7.3 循环群的属性#

设群 $\mathbb{G}=\langle g\rangle$ 是阶为 $n$ 的循环群。如果 $h=g^k$，则 $h$ 的阶为 $\frac{n}{d}$，其中 $d=\gcd(k,n)$。

设 $h$ 的阶是 $m$，则 $g^{km}=e$ 于是 $n\mid km\Rightarrow \frac{n}{d}\mid \frac{k}{d}m\Rightarrow \frac{n}{d}\mid m$，所以被 $\frac{n}{d}$ 整除的最小的数就是 $\frac{n}{d}$。

设群 $\mathbb{G}=\langle g\rangle$ 是阶为 $n$ 的循环群，则群 $\mathbb{G}$ 中恰有 $\varphi(n)$ 个生成元。

据此我们可以推出模 $n$ 乘法循环群有 $\varphi(\varphi(n))$ 个生成元。

7.4 找原根#

原根判定定理

$g$ 是原根，当且仅当 $\forall i,g^{\frac{\varphi(n)}{p_i}}\not\equiv 1\pmod {n},\varphi(n)=\prod p_i^{c_i}$。

最小原根的数量级是 $n^{0.25}$ 的。

习题#

7.4 如果 $p$ 是素数，则 $\mathbb{Z}_p$ 没有非平凡子群。

所有非单位元的元素的阶都是 $p$。

7.5 设 $n$ 为任意正整数，群 $\mathbb{Z}_n$ 的生成元 $r$ 满足以下条件 $\gcd(r,n)=1$。

设某个元素 $g$ 的阶为 $m$，则 $n\mid gm$，设 $\gcd(g,n)=d$ 则 $\frac{d}{n}\mid \frac{g}{d}m$ 即 $\frac{n}{d}\mid m$，这时 $d\ne 1$ 时 $m$ 一定小于 $n$。又群 $\mathbb{Z}_n$ 的阶是 $n$ 所以一定只有 $d=1$ 的元素才是生成元。

7.6 证明：如果群 $\mathbb{G}$ 没有非平凡子群，则群 $\mathbb{G}$ 是循环群。

任取 $g\in \mathbb{G},g\ne e$，则 $\langle g\rangle$ 是循环群，又 $\mathbb{G}$ 没有非平凡子群所以 $\langle g\rangle=\mathbb{G}$ 所以 $\mathbb{G}$ 是循环群。

7.8 证明：设 $\mathbb{G}$ 为任意群，且 $g\in G$。如果存在 $m,n\in \mathbb{Z}$ 使得 $g^m=1$ 且 $g^n=1$，则 $g^{\gcd(n,m)}=1$。

$g^{n-m}=1$。

8 陪集和拉格朗日定理#

8.1 陪集#

设 $\mathbb G$ 是群，$\mathbb H$ 是群 $\mathbb G$ 的子群。定义 $\mathbb H$ 的左陪集为 $g\mathbb H=\{gh:h\in\mathbb H\}$，其中，元素 $g\in\mathbb G$ 被称为代表元（Representative）。右陪集的定义类似：$\mathbb Hg=\{hg:h \in\mathbb H\}$。

证明费马小定理和欧拉定理。

$\mathbb{Z}_p^*$ 是 $\mathbb{Z}$ 的子群，那么 $a\mathbb{Z}_p^*$ 是一个陪集，而 $a\in \mathbb{Z}_p^*$，这时 $ah$ 会被吸收掉，于是 $a\mathbb{Z}_p^{*}=\mathbb{Z}_p^{*}$。

命题 8.1

设 $\mathbb G$ 是群，$\mathbb H$ 是 $\mathbb G$ 的子群。任取 $g_1,g_2\in \mathbb G$，则 $g_1\mathbb H=g_2\mathbb H$ 当且仅当 $g_2\in g_1\mathbb H$。

$$g_1h=g_2h'\\ g_2=g_1hh'^{-1}\in g_1\mathbb H\\ $$

命题 8.2 设 $\mathbb G$ 是群，$\mathbb H$ 是 $\mathbb G$ 的子群。对任意的 $g\in \mathbb G$，群 $\mathbb H$ 的阶与集合 $g\mathbb H$ 的阶相同。

$$h_1\ne h_2\\ gh_1\ne gh_2$$

命题 8.3 设 $\mathbb G$ 为群，$\mathbb H$ 是 $\mathbb G$ 的子群。任取不同的两个群元素 $g_1,g_2\in G$，则 $g_1\mathbb H=g_2\mathbb H$ 或 $g_1\mathbb H\cap g_2\mathbb H=\emptyset$。

$$\exist g_1h_1=g_2h_2\Rightarrow g_2=g_1h_1h_2^{-1}\\ g_2h_3=g_1h_1h_2^{-1}h_3\\ g_2\mathbb H=g_1\mathbb H\\ $$

命题 8.4 设 $\mathbb G$ 是群，$\mathbb H$ 是群 $\mathbb G$ 的子群。则子群 $\mathbb H$ 的所有左陪集将划分群 $\mathbb G$。

显然所有左陪集覆盖整个群 $\mathbb G$。

定义 指标

设 $\mathbb G$ 是群，$\mathbb H$ 是群 $\mathbb G$ 的子群。$\mathbb H$ 在群 $\mathbb G$ 上的指标（Index）定义为 $\mathbb H$ 在 $\mathbb G$ 上不相同的左陪集的个数，并记为 $[\mathbb G:\mathbb H]$。

8.2 拉格朗日定理#

设 $\mathbb G$ 是有限群，$\mathbb H$ 是 $\mathbb G$ 的子群，则 $\frac{|\mathbb G|}{|\mathbb H|}=[\mathbb G:\mathbb H]$。

证明由命题8.4显然得到。

推论 8.1 任意元素的阶 $\mathrm{ord}(g)\mid |\mathbb G|.$

推论 8.2 素数阶群任意元素均为生成元。

由推论 8.1 可得。

推论 8.3 设 $\mathbb H$ 和 $\mathbb K$ 是有限群 $\mathbb G$ 的子群，并且 $\mathbb K<\mathbb H<\mathbb G$，则 $[\mathbb G:\mathbb K]=[\mathbb G:\mathbb H][\mathbb H:\mathbb K]$。

$$[\mathbb G:\mathbb K]=\frac{|\mathbb G|}{|\mathbb H|}\frac{|\mathbb H|}{|\mathbb K|}=[\mathbb G:\mathbb H][\mathbb H:\mathbb K]$$

由拉格朗日定理可得，任意有限群 $\mathbb G$ 及其中元素 $g\in\mathbb G$，有 $g^{|\mathbb G|}=e$。这样即可证明费马小定理和欧拉定理。

9 同构，同态与商群*#

9.1 同构#

给定群 $(\mathbb G,\cdot )$ 和群 $(\mathbb H,*)$，如果存在一种双射 $\phi:\mathbb G \mapsto \mathbb H$，使得群操作得以保持，即：任取 $a,b\in G$，$\phi(a\cdot b)=\phi(a)*\phi(b)$。称群 $\mathbb G$ 与群 $\mathbb H$ 同构，并记为 $\mathbb G\cong \mathbb H$。映射 $\phi$ 被称为一种同构映射。

同构是等价关系，将所有群分成若干等价类。

定理 9.1 凯莱定理

每一个群都同构于一个置换群。

10 中国剩余定理#

10.1 数论角度下的中国剩余定理#

物不知数问题：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？
化解为线性方程组来表示即为：

$\begin{cases} x \equiv 2 \pmod 3\\ x \equiv 3 \pmod 5\\ x \equiv 2 \pmod 7\\ \end{cases}$

对于这个方程组我们可以对于每个方程构造一个数使得其模其它模数为0，模自己的模数为答案。

即对于上面的方程可以构造：

$\begin{cases} a_1=35\\ a_2=63\\ a_3=30\\ \end{cases}$

全部加起来即可得到一组特解 $x_0=128$。然后得到通解 $x=x_0+Mt, t \in \mathbb{Z}$。$M$ 是模数的最小公倍数。

可以得到最小正整数解：$x=23$。

通过这个例子我们可以得到下面的结论：

如果模数两两互素，设 $M=\Pi_{i=1}^{n}m_i, M_i=\frac{M}{m_i}$。根据古人的智慧我们可以构造出一个特解：$x_0=\sum\limits_{i=1}^{n}b_iM_i{M_i}{-1}$。

容易证明这个特解是对的，然后我们就可以得到通解：$x=x0+M$。

多数情况下模数不是质数，所以要用exgcd求逆元。

10.2 扩展中国剩余定理#

这个时候，我们就要每个方程轮流按顺序求解。

假设我们已经求出一个解$x=x_0+Mt, t \in \mathbb{Z}$。这个解满足前$i-1$个方程。现在我们将其和第$i$个方程合并。

具体操作就是将其代入第$i$个方程来解出得到未知数$t$的一个通解。

设第$i$个方程是形如$x \equiv a \pmod b$的。

解方程的过程：

$x_0+Mt \equiv a \pmod b$

$Mt \equiv a - x_0 \pmod b$

如果这个方程无解则整个方程组无解。

设 $g=\gcd(M,b)$

解得：$t=t_0+\frac{b}{g}t', t' \in \mathbb{Z}$。

带回 $x$ 的解，得：$x=x_0+M(t_0+\frac{b}{g}t')=x_0+Mt_0+lcm(M,b)t',t' \in \mathbb{Z}$。

将 $x_0$ 更新为 $x_0+Mt_0$，$M$更新为 $lcm(M,b)$ 即可。

第一个方程显然可以得到一组解$x=a+bt, t \in \mathbb{Z}$

10.3 群论角度下的中国剩余定理#

$n=pq$ 且 $p,q$ 是质数。

$$\mathbb Z_n\cong \mathbb Z_p\times \mathbb Z_q\\ \mathbb Z_n^*\cong \mathbb Z_p^*\times \mathbb Z_q^*\\ $$

11 二次剩余#

11.1 定义#

设 $p$ 是奇素数，$a$ 是与 $p$ 互质的整数，询问是否存在 $x$ 使得 $x^2\equiv a\pmod p$。

11.2 勒让德符号和欧拉准则#

定义 $a\bmod p$ 的勒让德符号为：

$$\left(\frac{a}{p}\right) = \begin{cases} 1(exist)\\ -1(not)\\ 0(p\mid a)\\ \end{cases}$$

欧拉准则：

$$\left(\frac{a}{p}\right)\equiv a^{\frac{p-1}{2}}\pmod p$$

当 $\left(\frac{a}{p}\right)=1$ 时，$\exist x,x^2\equiv a,(x^2)^{(p-1)/2}\equiv 1\Rightarrow a^{\frac{p-1}{2}}\equiv 1$。

否则，$a^{(p-1)/2}-1\not\equiv 0$，又 $0\equiv a^{p-1}-1=(a^{(p-1)/2}-1)(a^{(p-1)/2}+1)\Rightarrow a^{(p-1)/2}+1\equiv 0$。

推论

设 $p$ 是奇素数，则

$$\left(\frac{-1}{p}\right)= \begin{cases} -1&(p\bmod 4=-1)\\ 1&(p\bmod 4=1)\\ \end{cases}$$

二次互反律

$$\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)=(-1)^{\frac{(p-1)(q-1)}{4}}$$

11.3 Cipolla算法#

我们随机一个 $n$，令 $\omega=\sqrt{n^2-a}$。将数系扩充成 $\mathbb{F_\omega}$，相当于复数里面的 $i$。我们反复随机 $n$，直到 $n^2-a$ 不是一个二次剩余。然后大概可以证明这样的 $n$ 的大概有一半，所以期望随机二次既可以随机出一个，然后答案就是 $(n+\omega)^{\frac{p+1}{2}}$。

证明先考虑两个引理：

$$\omega^p=-\omega\\ a^p+b^p\equiv (a+b)^p\pmod p$$

第一个考虑拆成 $(\omega^2)^{\frac{p-1}{2}}\times \omega$，第二个考虑二项式定理展开。

然后这个证明就很显然了，直接暴力平方展开然后替换，最后是一个平方差的形式，相信大家都会。

显然 $x,-x$ 都是二次剩余。

提交记录

12 环和域#

12.1 环#

定义

环 $R$ 是一种包含两种运算的代数结构，分别称为加法和乘法。则加法是一个交换群，乘法满足交换律且存在单位元。乘法满足加法分配律。如果乘法也满足交换律，则称环 $R$ 是交换环。

如果乘法逆元存在且满足交换律，则称其为域 $F$。

13 有限域#

咕咕咕了

14 大数分解算法#

质因数分解
唯一分解定理
所有的合数都可以分解成下面的形式：

$p_1^{c_1} \times p_2^{c_2} \times \cdots \times p_m^{c_m}$，一般$p_1 < p_2 < \cdots <p_m$

试除法
枚举所有质数，然后判断是不是其因数，如果是再一直除下去求有多少个这个质因数。

注意枚举的因数只用到根号n，因为不可能有两个大于根号n的素因子。除到最后如果n不是1就说明n存在一个大于根号n的质因子，加到n的质因子序列中即可。

所以筛质数一般也只用筛到根号n。

Pollard-Rho
一个随机化算法，比较迷。

具体就是找到n的一个约数d，然后分治去求d的质因数分解和n/d的质因数分解。再用MR判断一下当前n是不是质数，如果是直接加到质因数序列即可。

至于怎么找到这个d，这就是随机化的思想了。

先搞出来一个x，y在[1,n-1]的范围内随机找，然后每次令x=f(x)，y=f(f(y))，直到1<gcd(|x-y|,n)<n就退出循环gcd(|x-y|,n)就是n的一个约数。

f(x)=(x+d)%n, d=random[1,n-1]。

这样做的时间复杂度大约是O(n^{\frac{1}{4}})

15 离散对数#