《浅谈 Splay 与 Treap 的性质及其应用》学习笔记
屎一样的一年还有两天就过去了呢。
听说要期末考,日了狗了。
感觉都阳了一周了还是没有回复到正常状态,真的挺讨厌的。今天随便找了篇论文假学习了一会儿。
由于懒,所以大量内容属摘抄。
《浅谈Splay与Treap的性质及其应用》学习笔记
1 Splay
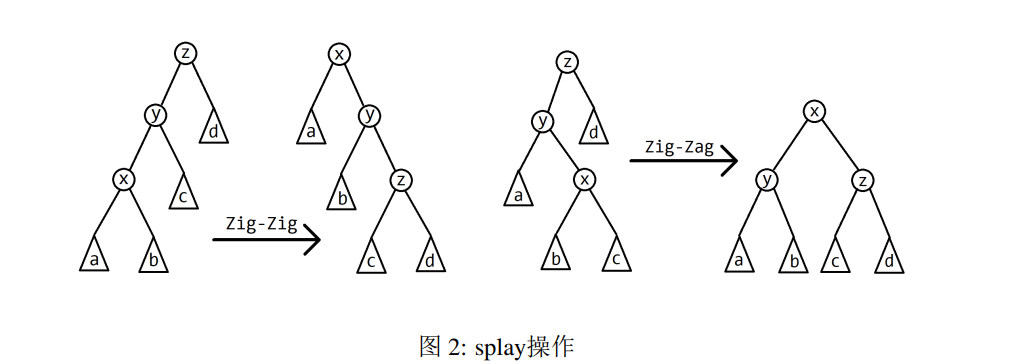
2 Treap
2.1 节点深度
考虑每个节点 \(i\) 在什么情况下会成为节点 \(x\) 的祖先。当 \(i\) 为 \(x\) 的祖先时,说明在 \(i\) 到 \(x\) 之间的节点的优先级都小于 \(i\) 。因此节点 \(x\) 的期望深度为
3 Finger Search
finger search 指的就是在数据结构中从某些特定的节点(也就是“finger”)开始查找
其他元素。
记 \(d(x,y)\) 表示两个元素 \(x,y\) 在集合中的排名之差。
下说明 \(\mathbf{finger search}\) 的复杂度为 \(polyd(x,y)\)。
3.1 Splay 上的 Finger Search
定理 3.1 (Dynamic Finger Theorem). 在一棵 \(n\) 个节点上的 Splay 上进行 \(m\) 次的插入、删除或
者查找操作的总时间为 \(O(n+m+\sum_{i=1}^{m}\log(d_i+1)\)。其中 \(d_i\) 表示第 \(i\) 次操作的元素与第 \(i−1\) 次操作的元素在该操作时的排名之差。第 \(0\) 次操作的元素可以视为初始的根节点。
论文原作者说他也不会证明。。。
3.2 Treap 上的 Finger Search
定理 3.2. 两个元素 \(x,y\) 在 Treap 上的路径长度是期望 \(O(\log(d(x,y)+1))\) 的。
证明和 2.1 的证明很像。

丢一个截图,明天再看。

3.3 应用
3.3.1 启发式合并
对于Splay,只需要把较小的一棵Splay中的元素按升序/降序的顺序中插入到另一棵Splay中。
对于Treap,同样把较小的一棵Treap中的元素按升序/降序的顺序插入到另一棵Treap中,每次插入时从上一个插入的位置开始进行一次 \(\mathbf{finger}\) \(\mathbf{search}\),找到新元素应插入的位置。具体实现时可以自顶向下地实现,这样就不需要记录每个节点的父指针。(ps 这里没太搞懂怎么不记父亲)
假设合并的两棵平衡树大小分别为 \(n,m(n\ge m)\)。那么这样合并时,除了第一次插入的耗时为 \(O(\log n)\) 外,其余插入的总耗时为 \(O(\sum_{i=2}^{m}\log (d_i+1))\)。
由于 \(\log\) 是凸函数,最坏情况为所有 \(d_i\) 相等,即 \(d_i=\dfrac{n}{m}\)。因此一次合并的复杂度就是 \(O(m\log \dfrac{n}{m})\)。
那对于一个元素,假设其在合并过程中的集合大小是 \(s_1,s_2,\dots,d_k\),那么合并其的复杂度也就是 \(O(\sum_{i=2}^{k}\log \dfrac{s_{i}}{s_{i-1}})=O(\log n)\)。
总的复杂度也就是 \(O(n\log n)\)。
ps:实际实现不用 finger search 毫无差异,但是比 set.insert() 要快多了。
3.3.2 维护答辩序列
我可能还是没太看懂treap快速分裂合并那个部分。
4 带权二叉树
额...不懂这一部分是干什么的?这个带权的意义不大啊。
4.4 多层嵌套问题
没太看懂嵌套了什么地方?树剖不就是树剖吗?
等我做会了这道题再来看看。
4.5 LCT
狗都不学。


