Intro to Blocks
Intro to Blocks
新瓶新酒,把之前所有遇到的分块的零零散散的内容都总结一下。
我也是不是啥数据结构大师,所以这篇 Tutorial 可能也没有啥深层次的理解。
可能有一些不属于分块的东西。本文芝士可能没有太明确的学习顺序,所以是可以乱序学的。
分块思想
其实也没有什么牛逼的东西,分块这个算法其实是一个思想,不是什么一定是 \(O(n\sqrt{n})\) 的什么算法。分块其实就是平衡思想,有的时候我们把信息分成若干个组,在组与零散的点中找平衡,这就是分块的基本思想。
那么需要解决的问题题就是组内信息的处理,组与组之间,组和零散信息之间如何合并。
自然根号
一些不需要特殊构造就存在根号结构。
数论分块
不想讲太多,结论就是 \(\lfloor\frac{n}{i}\rfloor\) 只有 \(O(\sqrt{n})\) 种不同的取值,且相同取值的数连续。\([l,\lfloor\frac{n}{\lfloor\frac{n}{l}\rfloor}\rfloor]\) 这一段的值都是 \(lfloor\frac{n}{l}\rfloor\)。
关于具体的证明可以看这里:https://oi-wiki.org/math/number-theory/sqrt-decomposition/
例 CQOI2007 余数求和
先来道简单一点的练练手
例 洛谷P6583 回首过去
https://www.cnblogs.com/zcr-blog/p/13157072.html
数论分块常用于莫比乌斯反演等数论题里,这里不过多解释。
和中不同数
设有 \(n\) 个数 \(a_1,a_2,\dots a_n\),他们的和是 \(m\),那么 \(n\) 个数最多有 \(O(\sqrt{m})\) 种不同的数。
启发式思想
https://www.luogu.com.cn/problem/P5576
结合字符串问题
https://www.luogu.com.cn/blog/command-block/str-ji-lu-cf204e-little-elephant-and-strings
https://www.luogu.com.cn/blog/command-block/str-ji-lu-loj6681-yww-yu-shu-shang-di-hui-wen-chuan
根号分治
暴力思想
假设一个问题有两种不同的方法,可以得到两种不同的复杂度,这个时候将数据分成两类,每类用适当的做法,以做到平衡总的复杂度的方法,就是根号分治。
为什么叫做暴力思想,因为通常有一种做法是暴力,另一种做法是另一种暴力/xyx
例 CF103D Time to Raid Cowavans
假设 \(n,q\) 同阶。两种暴力,一种是直接往后跳,复杂度 \(O(\frac{n}{k})\) 还有一种是枚举 \(k\),然后从后往前扫一遍 dp,复杂度 \(O(nk)\),于是平衡一下,取 \(k=\sqrt{n}\),小于的部分做第二种暴力,大于的部分做第一种暴力,复杂度为 \(O(n\sqrt{n})\)。注意这题的空间限制,所以不能开桶,要离线。有一点卡常。
例 CF1580C Train Maintenance
赛时没做出来真的可惜,当时还是太菜了。设定阈值 \(B=\sqrt{n}\),如果 \(x+y>B\) 就暴力跳然后差分。否则对于每个 \(x+y\) 维护一个数组,代表一个 \(x+y\) 周期每天维修的车的数量,然后在查询的时候枚举所有 \(\le B\) 的 \(x+y\),算出这个位置在周期里是第几个即可。
例 CF1039D You Are Given a Tree
这大概就是根号分治的暴力思想,接下来我们来看一些具体的应用场景(套路)。
对次数分治
例 CF444D DZY Loves Strings
https://www.luogu.com.cn/problem/P8330
对度数分治
对长度分治
https://www.luogu.com.cn/problem/CF587F
习题
IOI2009 regions
由于所有地区出现次数和是 \(n\),所以直接对出现次数分治,对于 \(r_1\) 出现次数大于 \(\sqrt{n}\) 的,暴力在树上扫一遍,就可以对于每个点求出有多少个祖先是 \(r_1\) 了。否则我们可以直接枚举每个 \(r_1\),然后记录他有多少个后代是 \(r_2\)。这可以离线枚举每个 \(r_2\),那这样就是有 \(O(n)\) 次修改,\(O(n\sqrt{n})\) 次询问,值域分块平衡复杂度,不会值域分块的可以先看后面值域分块的部分。
看到这种与 \(p\) 的大小有直接关系的题可以想想根号分治。思想其实很简单,就是设定一个阈值 \(k\),把大于其的和小于其的分开来讨论。对于这道题我们很容易想到一个暴力建边跑最短路的方法:从 \(b_i \rightarrow b_i + s \times p_i\) 连一条长度为 \(|s|\) 的边,我们将阈值设为 \(\sqrt{n}\),那么对于大于其的 \(p_i\) 最多会连 \(\sqrt{n}\) 条边。剩下的不是很好办,我们发现剩下的最多有 \(\sqrt{n}\) 个,我们考虑每 \(p_i\) 个点直接连一条边,不过这是错的,因为这个边是有向的。接下来就很妙了,建一个分层图,每个 \(p_i \le \sqrt{n}\) 都建一个,每层之间按上述方法连边,建一个第 \(0\) 层代表原来的图,如果有一只doge的 \(p_i \le \sqrt{n}\),那么就从第 \(0\) 层的 \(b_i\) 连向 \(p_i\) 层的 \(b_i\),代表其可以随意跳 \(p_i\),再从每一层的 \(b_i\) 连向第 \(0\) 层的 \(b_i\) 以方便换一只doge跳。
https://www.luogu.com.cn/problem/P5397
莫队
莫队的本质是路径规划,可以证明 \(k\) 维路径规划可以做到 \(O(n^{\frac{2k-1}{k}})\)
普通莫队
给你个一个长度为 \(n\) 的序列和 \(q\) 次询问,每次询问给你一个 \(l,r\),问在原序列区间 \([l,r]\) 内有多少个不同的数。可以离线。\(1 \le n,q \le 10^5\)。
算法1
在线做,每次遍历 \(l \rightarrow r\),统计每个数出现的次数,如果一个数的出现次数从 \(0 \rightarrow 1\) 的话答案就加一,如果从 \(1 \rightarrow 0\) 的话,答案就减一。这个算法的时间复杂度是:\(O(len \times q)\),\(len\) 是单次查询的区间长度,如果出题人用py造数据的话最优是可以单次 \(O(1)\)做的。
算法2
假设我们知道区间 \([1,5]\) 的答案,我们现在需要求出 \([2,6]\),那只需把 \(1\) 减掉,把 \(6\) 加上就可以在 \(O(1)\) 的时间内解决了。可是很遗憾这也是错的。只需搞一个 \([1,2], [9999,10000], [1,2], [9999,10000] \cdots\) 就可以卡死这个算法。
算法3
在算法2的提示下我们发现如果把询问离线,然后再排序就可以减少很多不必要的计算。如何来设计这个排序方法来达到最优的复杂度呢?这就是莫队做的事。
把原数列分块,块长为 \(\sqrt{n}\),最后一个块不够没关系。对询问排序时先按左端点所在块从小到大排序,对于同一块内的按右端点从小到大排序。
这样子如果我们可以在很短的时间内(通常是 \(O(1)\) 或者 \(O(\log{n}\)))从区间 \([l,r]\) 扩展到区间 \([l \pm 1,r \pm 1]\),对于一个块内左端点的扩展为 \(O(n)\)(从左到右再从右到左这样一直做),共有 \(\sqrt{n}\) 个块,所以左端点扩展的时间复杂度为 \(O(n\sqrt{n})\),因为右端点是有序的,所以每个块内右端点扩展最多是 \(O(n)\),所以右端点扩展的时间复杂度也为 \(O(n\sqrt{n})\),总的时间复杂度也就是 \(O(n\sqrt{n})\)了。
如果按上述排序方法可能不够快,原因是我们的右端点每次都是从最小到最大。如果我们可以让其从最小到最大再从最大到最小这样子可以省去很多冗余计算。即排序时相同块如果是奇数编号从小到大,偶数编号从大到小。
从这个例子我们可以看出普通的普通的莫队算法可以解决的问题:
只有询问且相互独立,可以快速从区间 \([l,r]\) 扩展到区间 \([l \pm 1,r \pm 1]\),允许离线。
关于块长和复杂度
之前的块长讲错了qaq,设快长为 \(t\),询问为 \(m\),序列长为 \(n\),则时间复杂度应为 \(O(mt + \frac{n^2}{t})\),由均值不等式可得当 \(mt=\frac{n^2}{t}\) 即 \(t=\frac{n\sqrt{m}}{m}\) 时有最小值 \(O(n\sqrt{m})\)。此时如果取块长为 \(\sqrt{n}\) 的话时间复杂度是 \(O((n+m)\sqrt{n})\) 的,\(m\) 比 \(n\) 大很多时有明显的优势。
练习
回滚莫队
首先我们要理解回滚的意思。
回滚指的是程序或数据处理错误,将程序或数据恢复到上一次正确状态的行为(以上摘自百度百科
简单来说就是撤销操作。回滚莫队是用来解决扩展容易删除难或删除容易扩展难的问题(如果都难就别用莫队了。
第一种情况:扩展易,删除难。
例题:歴史の研究
因为接口问题这题再luogu上可能无法提交,但也不妨碍我们做题。
考虑莫队怎么扩展,我们发现想从\(l \rightarrow l-1\)或\(r \rightarrow r+1\)只用算出取值和之前的最大值比较就行。可是删除操作就不太好做了,你有可能删掉的就是之前的最大值。当然,估计可以用维护次大值的方法,但这样太麻烦了,我们考虑稍微暴力一点的做法。
首先排序的时候先按l的块排,同一块内的按r从小到大,这样r就不会减少了。对于l的部分,我们先重置答案为r跑的答案,然后我们每次都从当前询问的l跑到当前块的最后来增加,这样子也就只有增加操作。然后就是回滚的部分了,把l增加的值删掉就行了。
每到一个不同的块r可能会变小,这时要重置r的答案然后所有r的值也用删掉。时间复杂度还是\(O(n\sqrt{n})\)
第二种情况:扩展难,删除易
这题我没写,思路纯属口胡。
此题删除一个数,看它剩余的个数是不是0,如果是则和当前最小值比较一下就行。
然后类似情况1。对于每一块我们按r从大到小排序,然后再从当前块最左端加到序列末尾,求一遍最小值(\(O(n)\))。之后r就从n开始删,l每次从左端点删到当前询问的l,然后再复原即可。
回滚莫队可以看成l和r分开来做的一种莫队,使得r单调,l每次暴力且范围较小。
带修莫队
例题:[国家集训队]数颜色
其实懂了最基础的莫队其他版本都是在其基础上稍微修改。
因为有了修改操作,我们不妨在每个询问再加上一维“已经修改了几次”,即时间维。
于是变成了三维莫队
类比普通莫队,我们先按l所在块排序,再按r所在块排序,最后按t从小到大排。
对于普通的l和r的扩展就和以前一样。
对于t的扩展如果修改在当前区间内则改掉然后重新把这个点加进去,所以我们就要记录每个修改是从什么改成什么,撤销就把它改回去就行。
时间复杂度的分析:
当块长为\(n^{\frac{2}{3}}\)次方时最优,为\(O(n^{\frac{5}{3}})\)。
至于例题的扩展部分因为太模板了就不讲了。
例题的代码(很良心了)
树上莫队
欧拉序实现路径统计
欧拉序有两种,另外一种可以用来求lca,千万别搞混了。
这种欧拉序我们在进入这棵子树时添加,出子树时再加进去得到,比如下图。
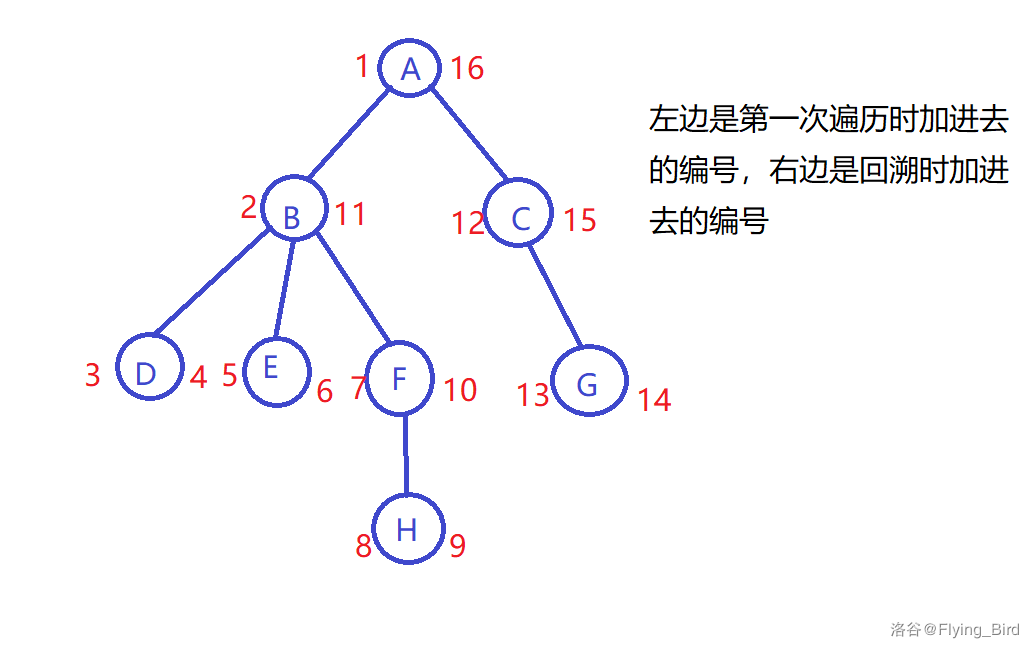
容易发现这是个2n的序列。我们得到的序列是:ABDDEEFHHFBCGGCA
然后我们便把树变成了一个序列,可以转换成序列上的查询问题。
对于每个点我们记录它第一次遍历的序号记为\(L_i\),第二次回溯的编号记为\(R_i\)。然后我们发现对于每个询问\(u,v\),若\(u\)是\(v\)的祖先,即其最近公共祖先为\(u\),那么区间\([L_u, L_v]\)中出现一次的点均为路径上的点(注意这里是出现一次的点)。为了不出现v是u的祖先这种情况,我们可以强制u的L更小,即交换了u,v。如果不是的话,我们发现路径上的点即为区间\([R_u,L_v]\)中只出现一次的点并上它们的lca。
至于怎么实现,我们可以维护一个数组来维护某个点有没有被改过,如果被改过就把改的删掉,如果没有就改。
先序实现子树统计
子树一定是一段连续的区间,然后就没了。
一个简单的询问的树上加强版,树上的子树可以分为是当前根的祖先和其它,第二种不用变,第一种与树上儿子取个补集就行。
树上带修莫队
套在一起就行了。
一些处理技巧
主要是扩展不易想到
考虑扩展的性质(这也是最难的),降低时间复杂度。实在不行就回滚(或者莫队二离
先把所有的信息统计出来,再求答案。这时可以对值域分块然后在\(O(\sqrt{n})\)的复杂度内求解。
多个区间的询问,考虑容斥拆区间拆成\([1,x],[1,y]\)的形式,本质上只有一个区间\([x,y]\)。
用bitset来帮助处理,[Ynoi2016]掉进兔子洞
一些例题
看起来可以莫队做,关键是如何扩展删除。
删除可以看做减去扩展的,所以我们只考虑扩展的。
因为左边扩展是和右边一样的所以我们只考虑右边。
我们记录每个数 \(a_i\) 前面第一个小于它的数 \(a_j\),显然 \((j,i]\) 这一部分都是 \(a_i\)。我们跳到 \(j\) 继续做刚刚的事。这是一个朴素的想法,显然一个单调上升的序列就可以把我们卡成 \(n^2\)。
我们发现这其实形成了一个树形结构。那么显然我们可以在树上做前缀和,然后倍增找到第一个。单次扩展时间复杂度稳定 \(O(\log{n})\)。可是这样子过不去这题,实测 \(0\) 分。
我们发现这个最浅节点一定是最小的节点,于是可以rmq \(O(1)\) 做,然后这题就做完了。
扫描线莫队(莫队二次离线)
前言
咕了很久想学,今天终于有时间来看了。
解决的问题
对于一般的莫队,我们一般要求单次扩展需要 \(O(1)\) 的复杂度,但是通过二次离线莫队(扫描线莫队),我们可以在 \(O(nk)\) 的时间复杂度,\(O(n)\) 的空间复杂度内预处理所有扩展,其中 \(O(k)\) 是向外扩展一次的复杂度。当然二次离线莫队还有一些别的要求,我会在之后的部分提到。
思想
考虑莫队向右扩展(其他类似)的过程,将 \((l,r)\to (l,r+1)\)。会有 \(r+1\) 对区间 \([l,r]\) 产生贡献,
Template & Practice
关于跑莫队的部分,我们把所有询问存到一个 vector 里面,分别代表(对第一种做解释) \(F(q[i].l,r)\) 到 \(F(l-1,r)\),系数是 \(1/-1\),然后对第 \(i\) 个询问做贡献。\(p\) 数组是 \(F(x,x-1)\),注意到大部分时候 \(F(x,x)=F(x,x-1)\) 所以只需预处理一种。
for(int i=1,l=1,r=0;i<=m;i++){
if(l>q[i].l)vec[r].pb(q[i].l,l-1,1,i);
while(l>q[i].l)q[i].ans-=p[--l];
if(r<q[i].r)vec[l-1].pb(r+1,q[i].r,-1,i);
while(r<q[i].r)q[i].ans+=p[++r];
if(l<q[i].l)vec[r].pb(l,q[i].l-1,-1,i);
while(l<q[i].l)q[i].ans+=p[l++];
if(r>q[i].r)vec[l-1].pb(q[i].r+1,r,1,i);
while(r>q[i].r)q[i].ans-=p[r--];
}
例 \(1\) LG4887
给定长为 \(n\) 的序列 \(a\) 和 \(m\) 组询问,查询区间 \([l,r]\) 中有多少 \(popcount(a_i\bigoplus a_j)=k\)
没有强制在线,\(1\le n,m\le 10^5,0\le a_i< 16384\)。
考虑预处理出所有 \(popcount(i)=k\) 的数 \(b\),注意到 \(a\bigoplus b=c\Leftrightarrow a=b\bigoplus c\),于是就很好处理了。
注意如果 \(F(x,y)\) 的 \(x\le y\) 且 \(k=0\) 那么 \(x\) 不能对自己做贡献,要减去 \(1\)。
例2 LG5047
给定长为 \(n\) 序列 \(a\) 和 \(m\) 次询问,每次询问一个区间的逆序对数
\(1\le n,m\le 10^5,1\le a_i\le 10^9\)
首先可以离散化,然后容易发现每次扩展只需知道一个区间里有几个数比它大(小),这显然可以拆成两部分,所以可以莫队二次离线。扫描线的时候使用根号分治,可以做到 \(O(1)\) 询问。
操作分块
操作分块主要应用在一类修改不好做的数据结构问题中。具体来讲,我们每 \(B\) 个操作分成一个组,做完这个组后进行对整体的重构。修改对询问的贡献分成两个部分,第一部分是之前的块对询问的贡献,由于已经重构,所以这个贡献是静态的。第二个部分是块内的贡献,这一部分不会超过块大小,所以可以直接暴力处理。
有些时候块内暴力也不是很容易,这个时候需要用回滚莫队的思想。
直接讲起来很抽象,不妨看几道题。
例 CF1588F Jumping Through the Array
问题很显然可以被看成是在置换环上做。但是这个置换环会变化,但每次变换的其实很少,所以考虑对操作进行分块。对于块里面的修改,我们把这些点看成关键点,而所有跟在关键点后面的点在这个块的修改里面都会和关键点同步修改查询,所以这些点其实可以缩成一个点,这样就只有 \(O(B)\) 个点了,直接暴力操作。
由于修改的最多只有 \(O(B)\) 个环,所以直接询问的时候直接枚举每个缩起来的点,查询这个点和询问区间的交集大小。code
例 APIO2019 桥梁
首先对操作分块,对于不用修改的边,建立kruscal重构树。然后每次询问的时候找到可以到的被修改的边,这个时候就扩展了可以到的点。然后继续找下去,复杂度 \(O(B\log n)\),那么总的复杂度就是 \(O(\frac{n^2\log n}{B}+nB\log n)\),取 \(B=\sqrt{n}\),得到复杂度 \(O(n\sqrt{n}\log n)\)。
我这个方法有点麻烦,其实不用显性地建出克鲁斯卡尔重构,排序之后按顺序加入并查集,再配合一个可撤销并查集即可。code
例 Ynoi2019 魔法少女网站
序列分块
数列分块入门
数列分块入门1
过于基础,直接上代码。
数列分块入门2
如果一个块是有序的那么我们显然可以二分查找,而如果一整个块同时加上某个数是不会改变相对顺序的。所以我们每次只在修改不完整的块时从新sort那个区间。查询时对于完整每个块二分,每个不完整直接暴力,如果块长为 \(\sqrt{N}\) 的话时间复杂度是:\(O(n\sqrt{N}\log{\sqrt{N}})\)。
数列分块入门3
类似数列分块2,二分找到一个最大就行。
数列分块入门4
这题恐怕是分块最最基础的操作了。
对于分块萌新我还是讲一下吧。
类似线段树的操作(希望你学过线段树),我们把区间分成很多个块,线段树是\(\log{n}\)个,我们分块就更暴力一点,直接在原数组上分\(\sqrt{n}\)个块。每个块都可以直接操作,而多余的边角料不会超过\(\sqrt{n}\)直接暴力就好。时间复杂度为\(O(n\sqrt{n})\)
数列分块入门5
开方操作不会有很多次,如果一个块内的数都是0或1这个块就不用执行开方操作,否则暴力开方。可以证明最多不超过6次。
数列分块入门6
这题我觉得块状链表可做。
块状链表就是一个链表,每个指向一个长度为\(\sqrt{n}\)级别的数组,具体结构如下图所示。
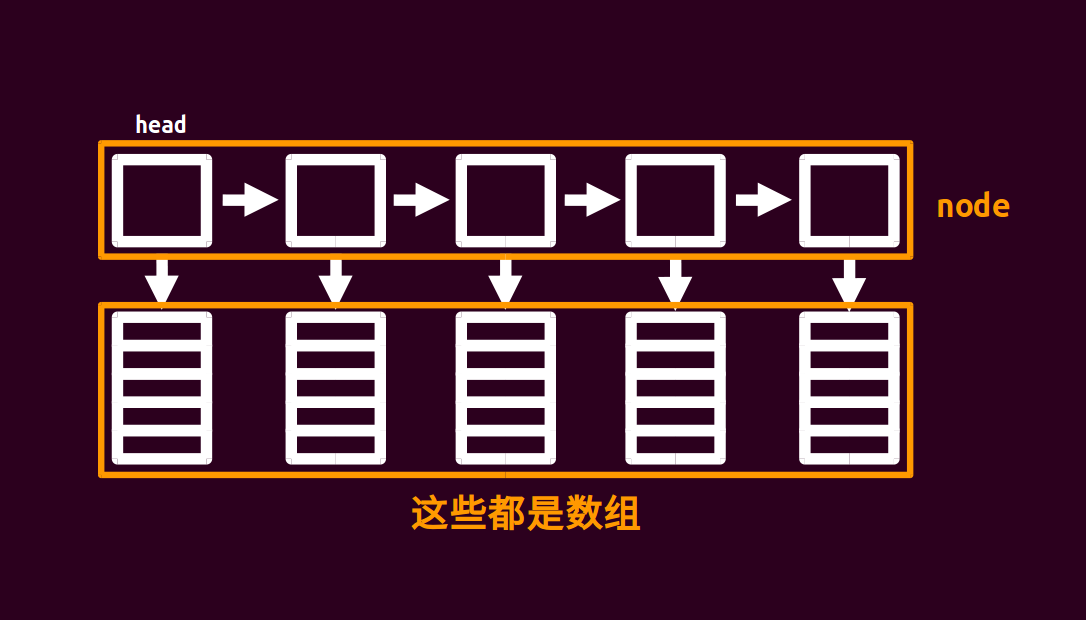
具体操作我们每个数组开\(2 \times \sqrt{n}\),要支持分裂操作,其实就是当前大小大于等于 \(2 \times \sqrt{n}\) 就新建一个node,把后面的放进去。
插入就暴力找到改在哪个位置插入,这是\(O(\sqrt{n})\)的,查询也就是暴力就行,块状链表所有操作都是\(O(\sqrt{n})\)。
此题还可用平衡树维护区间来做,用fhq-treap可以很简单地维护。
数列分块入门7
线段树经典题,看看我们能不能用类似的方法用分块做。
其实是一样的,乘法操作就一起乘就好了。
数列分块入门8
好像和第5题一样,不太会证复杂度
数列分块入门9
只会回滚莫队,哭了。
值域分块
块状链表
树分块
二维分块
杂题
References
这篇总结的实在太全了 分块指北 Dr.Zhou
还有 cmd 大佬的总结 分块相关杂谈

