拉格朗日乘数法
前言
正文
拉格朗日乘数法
求多元函数 \(F\) 的极值。满足 \(\varphi=0\)。再引入一个变量 \(\lambda\)然后令 \(F'=F+\lambda\varphi\)。然后对它的每个元素求偏导,并令其为 \(0\)。解出来的值即为极值。
但是这并不能求最小和最大,还要讨论一下。
正确性:对 \(\lambda\) 求偏导就可以得到约束条件,然后 \(\lambda\) 的值不会影响函数值。
证明什么的就百度一下吧。
- 一个具体的例子
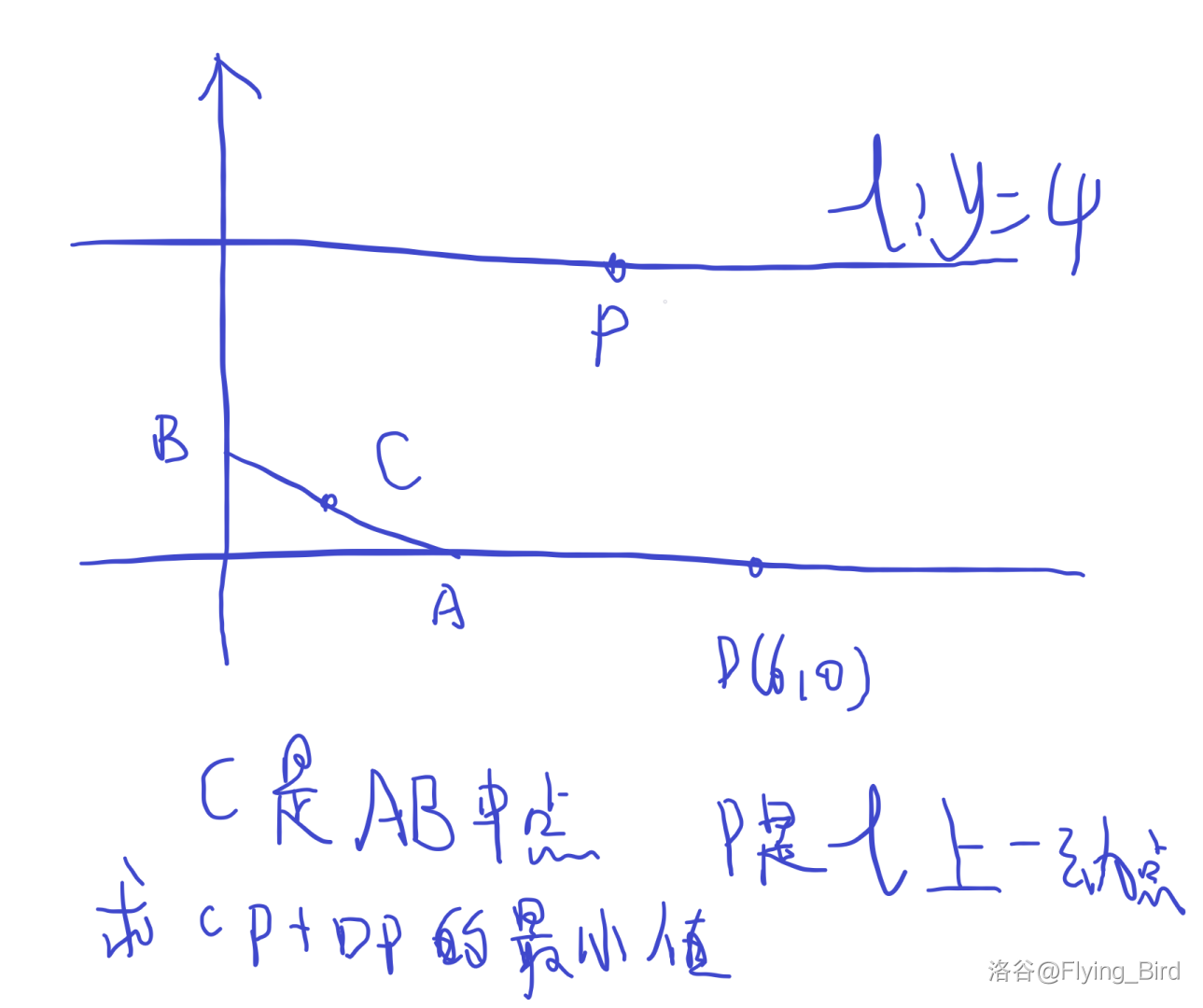
\(\text{AB}=2\)。
这是我的一道思博数学作业,显然 \(C\) 在以原点为中心,半径为 \(2\) 的圆上。然后就做完了。
我们考虑用代数去解决它:
设 \(A(x,0),B(0,y),C(\frac{x}{2},\frac{y}{2})\)。
\[\begin{aligned}
F(x, y)=(6-\frac{x}{2})^2+(8-\frac{y}{2})^2\\
\varphi(x,y)=x^2+y^2-4\\
ans=\sqrt {F(x,y)}\\
F(x,y,\lambda)=(6-\frac{x}{2})^2+(8-\frac{y}{2})^2+\lambda(x^2+y^2-4)
\end{aligned}
\]
然后你对其每一项求偏导,并令其为 \(0\)。
\[\begin{cases}
\frac{x}{2}+\lambda x=6\\
\frac{y}{2}+\lambda y=8\\
x^2+y^2=4\\
\end{cases}
\]
然后解就好了,最后答案是 \(9\)。
OI 一点的应用
【LG2179】

