亿些原古博客汇总 II
之前那个太满了编辑一下卡一年所以就新开一个。
[USACO12FEB]Nearby Cows G [2]
一句话题意:给你一棵 \(n\) 个点的树,点带权,对于每个节点求出距离它不超过 \(k\) 的所有节点权值和 \(m_i\) 。
\(1 \le n \le 10^5\)
定睛一看这就是今年省选B卷D1T2的60pts数据嘛。
k的范围很小,可以用\(O(nk)\)的算法水过去。其实就是换根dp。
令\(dp[u][k]\)代表u到其子树内距离为k的点的权值和,有\(dp[u][k]+=dp[v][k-1]\)。
然后考虑怎么从父亲扩展到儿子,其实就是一步容斥:\(f[v][k]=dp[v][k]+f[u][k-1]-dp[v][k-2]\)。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 100010;
const int K = 22;
const int inf = 0x3f3f3f3f;
template <typename T> void read(T &x) {
T w = 1;
char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') w = -1;
for (x = 0; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
x *= w;
}
struct node{
int pre, to;
}edge[N << 1];
int head[N], tot;
int n, k;
int dp[N][K], f[N][K];
void add(int u, int v) {
edge[++tot] = node{head[u], v};
head[u] = tot;
}
void dfs1(int x, int fa) {
for (int i = head[x]; i; i = edge[i].pre) {
int y = edge[i].to;
if (y == fa) continue;
dfs1(y, x);
for (int j = 1; j <= k; j++) {
dp[x][j] += dp[y][j - 1];
}
}
}
void dfs2(int x, int fa) {
f[x][0] = dp[x][0];
for (int i = head[x]; i; i = edge[i].pre) {
int y = edge[i].to;
if (y == fa) continue;
for (int j = 1; j <= k; j++) {
if (j > 1) f[y][j] = dp[y][j] + (f[x][j - 1] - dp[y][j - 2]);
else f[y][j] = dp[y][j] + (f[x][j - 1]);
}
dfs2(y, x);
}
}
int main() {
read(n); read(k);
for (int i = 1, u, v; i < n; i++) {
read(u); read(v);
add(u, v);
add(v, u);
}
for (int i = 1; i <= n; i++) read(dp[i][0]);
dfs1(1, 0);
for (int i = 1; i <= k; i++) f[1][i] = dp[1][i];
dfs2(1, 0);
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= k; j++) {
f[i][j] += f[i][j - 1];
}
printf("%d\n", f[i][k]);
}
return 0;
}
[USACO10MAR]Great Cow Gathering G [2]
换根dp模板题。
同时记录\(sz[u]\)代表\(u\)的子树内有多少奶牛,那转移时即为\(dp[u]=dp[v]+sz[v] \times val(u,v)\)。
注意开long long。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
const ll inf = 0x7f7f7f7f7f7f7f7f;
template <typename T> void read(T &x) {
T f = 1;
char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
for (x = 0; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
x *= f;
}
template <typename T> void cmin(T &x, T y) {if (y < x) x = y;}
struct node{
int pre, to;
ll val;
}edge[N << 1];
int head[N], tot;
int n;
int c[N];
ll dp[N], sz[N];
ll ans = inf;
void add(int u, int v, int l) {
edge[++tot] = node{head[u], v, l};
head[u] = tot;
}
void dfs1(int x, int fa) {
sz[x] = c[x];
for (int i = head[x]; i; i = edge[i].pre) {
int y = edge[i].to;
if (y == fa) continue;
dfs1(y, x);
sz[x] += sz[y];
dp[x] += dp[y] + sz[y] * edge[i].val;
}
}
void cut(int x, int y, int val) {
dp[x] -= dp[y] + sz[y] * val;
sz[x] -= sz[y];
}
void link(int x, int y, int val) {
dp[x] += dp[y] + sz[y] * val;
sz[x] += sz[y];
}
void change_root(int x, int y, int val) {
cut(x, y, val);
link(y, x, val);
}
void dfs2(int x, int fa) {
cmin(ans, dp[x]);
for (int i = head[x]; i; i = edge[i].pre) {
int y = edge[i].to;
if (y == fa) continue;
change_root(x, y, edge[i].val);
dfs2(y, x);
change_root(y, x, edge[i].val);
}
}
int main() {
read(n);
for (int i = 1; i <= n; i++) read(c[i]);
for (int i = 1, a, b, v; i < n; i++) {
read(a); read(b); read(v);
add(a, b, v);
add(b, a, v);
}
dfs1(1, 0);
dfs2(1, 0);
printf("%lld", ans);
return 0;
}
Censoring「USACO 2015 Feb」[2]
题目描述
有一个S串和一个T串,长度均小于1,000,000,设当前串为U串,然后从前往后枚举S串一个字符一个字符往U串里添加,若U串后缀为T,则去掉这个后缀继续流程。
输入格式
包含两行,第一行为S串,第二行为T串
输出格式
输出题目要求的字符串序列
样例
输入样例
whatthemomooofun
moo
输出样例
whatthefun
讲一下题意:
拿样例模拟一下,u往后添加一直到"whatthemomoo"时把末尾的"moo"删掉->"whattemo",之后又添加一个“o”,注意是这whatthemomoo(o)fun个“o”。变成"whatthemoo",再把moo删掉变成"whatthe"。最后加上fun,所以输出是"whattefun"。
这道题其实就是一道模拟+kmp(默认你们都会kmp)。用一个数组f纪录主串每个位置i它的后缀和模式串的前缀的最大匹配长度。删除就是回到i-m(模式串长度),然后j(匹配长度)回到fi-m即可。
代码也很好写。
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n, m, nxt[1000100], f[1000100], l;
char u[1000100], s[1000100], t[1000100];
int main() {
scanf("%s%s", s + 1, t + 1);
n = strlen(s + 1), m = strlen(t + 1);
for (int i = 2, j = 0; i <= m; i++) {
while (j && t[i] != t[j + 1]) j = nxt[j];
if (t[i] == t[j + 1]) j++;
nxt[i] = j;
}
for (int i = 1, j = 0; i <= n; i++) {
u[++l] = s[i];
while (j && u[l] != t[j + 1]) j = nxt[j];
if (u[l] == t[j + 1]) j++;
f[l] = j;
if (j == m) l -= m, j = f[l];//删除操作
}
for (int i = 1; i <= l; i++) cout << u[i];
return 0;
}
题目描述
串是有限个小写字符的序列,特别的,一个空序列也可以是一个串。一个串 P 是串 A 的前缀,当且仅当存在串 B,使得 A = PB。如果 P != A 并且 P 不是一个空串,那么我们说 P 是 A 的一个 proper 前缀。
定义 Q 是 AA 的周期,当且仅当 Q 是 A 的一个 proper 前缀并且 A 是 Q+Q 的前缀(不一定要是 proper 前缀)。比如串 abab 和 ababab 都是串 abababa 的周期。串 A 的最大周期就是它最长的一个周期或者是一个空串(当 A 没有周期的时候),比如说,ababab 的最大周期是 abab。串 abc 的最大周期是空串。
给出一个串,求出它所有前缀的最大周期长度之和。
输入格式
第一行一个整数 kk,表示串的长度。
接下来一行表示给出的串。
输出格式
输出一个整数表示它所有前缀的最大周期长度之和。
样例
样例输入
8
babababa
样例输出
24
数据范围与提示
对于全部数据,1 < k < 10^6
OKR-Periods of Words「POI 2006」[4]
解释一下题意:
跑一遍样例,babababa的前缀对应的最大周期长度分别是是00224466
如果你还没有看懂就只好自己yy一下了。
拿bababa来说,它的最大周期是baba不能为自己也不能为空串。
那我们很容易发现一个奇妙的性质那就是一个串的最大周期长度=len-最小前缀==后缀(非空)长度。
证明;
设一个串为a1,a2,a3……am,它的最小非空前缀等于后缀的长度为n
则显然可以取a1a(m-n)作为周期。因为a(m-n+1)a(m)=a1an(定义),所以a1am是a1an+a1an的前缀。
并且这个周期显然最大(n最小,m-n最大)。
这样这道题就很简单了,不过注意有可能会超时。这里要用dp的思想。dp[i]表示以i为结尾的前缀最小前缀==后缀长度,显然dp[i] = dpnxt[i].
这样就珂做了。
#include <iostream>
using namespace std;
long long k, l;
long long f[1000100];
long long nxt[1000100], ans;
char s[1000100];
int main() {
//freopen("test.in", "r", stdin);
cin >> k;
scanf("%s", s + 1);
for (long long i = 2, j = 0; i <= k; i++) {
while (j && s[j + 1] != s[i]) j = nxt[j];
if (s[i] == s[j + 1]) j++;
nxt[i] = j;
}
for (long long i = 2; i <= k; i++) {
f[i] = f[nxt[i]];
if (f[i] == 0 && nxt[i] != 0) {
long long l = nxt[i];
if (l == 0) continue;
while (nxt[l]) {
l = nxt[l];
}
f[i] = l;
} else if (f[i] == 0) {
continue;
}
ans += i - f[i];
}
cout << ans;
return 0;
}
跳蚤[BZOJ4310] [5]
看到让最大的最小我们就想到二分答案,二分答案在原字符串的所有不同子串中的排名。知道了排名,我们用后缀数组就很好求出答案串是什么(记录其在原串中的起始位置和结束位置),具体方法见代码。
这里还有一点要考虑的是二分的上界也就是子串的个数。其实这很好求就是∑n-sa[i]+1-height[i[。毕竟所有的子串都是一个后缀的前缀,对于一个后缀sa[i],他有n-sa[i]+1个前缀,但是有height[i]个前缀与前面的重复,已经算过了,就得减掉。
然后我们来考虑如何判定。这里我默认大家都会求LCP(LCP(i, j)=min{height[k]}(rank[i]<k<=rank[j]),然后用ST表nlogn预处理,O(1)时间内求出LCP)。记录一个cut=i代表你上次在i-1和i之间切了一刀,令cut的初值为n+1。再记录一个cnt代表切了多少次,如果cnt>=k则不成立(这里注意切了cnt到右cnt+1个块,所以是>=)。每次判定先求出当且串的起始和结束位置记为L, R,然后再从后往前枚举后缀i,求出i和L的LCP。若LCP==0,则判断s[L]和s[i]的大小关系,若s[i]>s[L]则返回false(根据题目要求s[L…R]应是一个快内最大的)。求min{LCP, cut - i, R - L + 1}。若cut-i最小,则说明上次剪的地方到现在这一段都是相同的(<LCP)或者比当前串还短(<R-L+1),此时这个位置一定不需要剪,直接continue。若R-L+1最小或者LCP最小且s[L+LCP]<s[i+LCP]时我们就需要分块。令cut = i + 1,cnt++,然后再判断cnt与k的关系即可。
上代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 100010;
ll k;
ll n, m;
ll sa[N], rnk[N], v1[N], v2[N], sum[N], height[N];
ll st[N][21];
char s[N];
bool cmp(ll *t, ll a, ll b, ll l) {
return t[a] == t[b] && t[a + l] == t[b + l];
}
void da() {
ll i, j, p = 0;
for (i = 1; i <= m; i++) sum[i] = 0;
for (i = 1; i <= n; i++) sum[rnk[i] = s[i]]++;
for (i = 2; i <= m; i++) sum[i] += sum[i - 1];
for (i = n; i >= 1; i--) sa[sum[rnk[i]]--] = i;
for (j = 1; j <= n; j *= 2, m = p) {
for (p = 0, i = n - j + 1; i <= n; i++) v2[++p] = i;
for (i = 1; i <= n; i++) if (sa[i] > j) v2[++p] = sa[i] - j;
for (i = 1; i <= n; i++) v1[i] = rnk[v2[i]];
for (i = 1; i <= m; i++) sum[i] = 0;
for (i = 1; i <= n; i++) sum[v1[i]]++;
for (i = 2; i <= m; i++) sum[i] += sum[i - 1];
for (i = n; i >= 1; i--) sa[sum[v1[i]]--] = v2[i];
for (swap(rnk, v2), rnk[sa[1]] = 1, p = 2, i = 2; i <= n; i++) {
rnk[sa[i]] = cmp(v2, sa[i - 1], sa[i], j) ? p - 1 : p++;
}
}
}
void calheight() {
ll i, j, p = 0;
for (i = 1; i <= n; i++) {
if (p) p--;
j = sa[rnk[i] - 1];
while (s[i + p] == s[j + p]) p++;
height[rnk[i]] = p;
}
}
void st_pre() {
for (ll i = 1; i <= n; i++) st[i][0] = height[i];
for (ll j = 1; j <= 20; j++) {
for (ll i = 1; i <= n; i++) {
if (i + (1 << (j - 1)) > n) break;
st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
}
ll LCP(ll l, ll r) {
if (l == r) return n - sa[l] + 1;
if (l > r) swap(l, r);
l++;
ll kk = log(r - l + 1) / log(2);
return min(st[l][kk], st[r - (1 << kk) + 1][kk]);
}
ll pos_l, pos_r, ans_l, ans_r;
void get_string(ll mid) {
for (ll i = 1; i <= n; i++) {
ll tmp = n - sa[i] - height[i] + 1;
if (mid > tmp) {
mid -= tmp;
} else {
pos_l = sa[i];
pos_r = sa[i] + height[i] - 1 + mid;
return;
}
}
}
bool check() {
for (ll i = n, cut = n + 1, cnt = 0; i >= 1; i--) {
ll lcp = LCP(rnk[pos_l], rnk[i]);
if (lcp == 0 && s[i] > s[pos_l]) return false;
lcp = min(lcp, min(pos_r - pos_l + 1, cut - i));
if (lcp == cut - i) continue;
if (lcp == pos_r - pos_l + 1 || s[i + lcp] > s[pos_l + lcp]) {
cnt++;
cut = i + 1;
if (cnt > k) return false;
}
} return true;
}
int main() {
scanf("%lld%s", &k, s + 1);
k--;
n = strlen(s + 1);
m = 200;
da();
calheight();
st_pre();
ll l = 1, r = 0;
for (ll i = 1; i <= n; i++) {
r += n - sa[i] - height[i] + 1;
}
while (l <= r) {
ll mid = (l + r) >> 1;
get_string(mid);
if (check()) {
ans_l = pos_l;
ans_r = pos_r;
r = mid - 1;
} else {
l = mid + 1;
}
}
for (ll i = ans_l; i <= ans_r; i++) {
cout << s[i];
}
return 0;
}
Samjia 和矩阵[loj6173] [5]
传送门
本题要求本质不同的子矩阵,即位置不同也算相同(具体理解可以看样例自己yy)。
我们先看自己会什么,我们会求一个字符串中不同的子串的个数。我们考虑把子矩阵变成一个字符串。
先枚举矩阵的宽度,记为w(1<=w<=m)。再把一行之内的连续的w的字符用字符串hash哈成一个整数,再把这个整数hash成一个较小的数(相当于之前字符串的一个字符)。
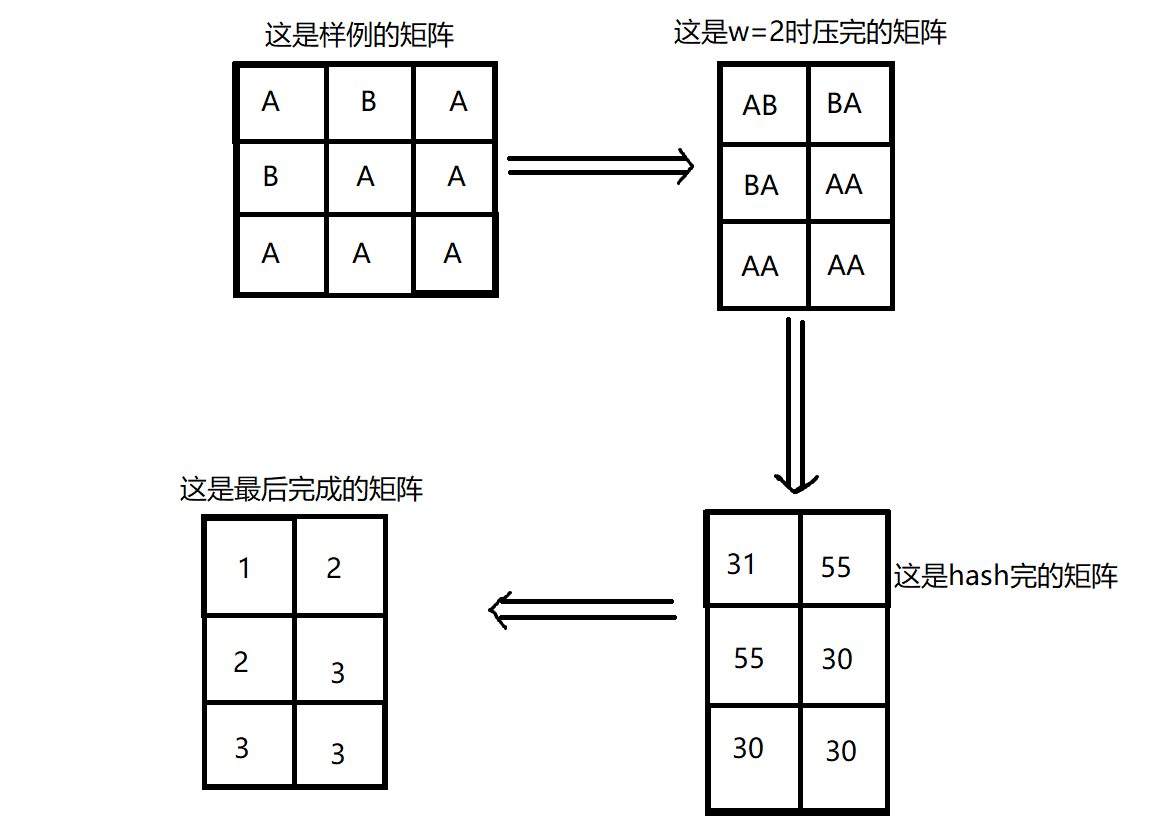
把最后完成的矩阵在把没一列接起来,形成一个字符串(每列后要加一个字符如:1 2 3 4 2 3 3 5)。然后对这个串求我们会的子串个数(减去height值)即可。
#include <iostream>
#include <cstdio>
#include <map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll N = 120, M = 120;
const ull P = 13331;
ll len, tot, ans;
ll n, m;
ll s[N * M], rnk[N * M], sa[N * M], sum[N * M], v1[N * M], v2[N * M], height[N * M];
char arr[N][M];
ull _hash[N][M];
map<ull, ll> mp;
bool cmp(ll *t, ll a, ll b, ll l) {
return t[a] == t[b] && t[a + l] == t[b + l];
}
void da() {
ll i, j, p = 0;
for (i = 1; i <= tot; i++) sum[i] = 0;
for (i = 1; i <= len; i++) sum[rnk[i] = s[i]]++;
for (i = 2; i <= tot; i++) sum[i] += sum[i - 1];
for (i = len; i >= 1; i--) sa[sum[rnk[i]]--] = i;
for (j = 1; j <= len; j *= 2, tot = p) {
for (p = 0, i = len - j + 1; i <= len; i++) v2[++p] = i;
for (i = 1; i <= len; i++) if (sa[i] > j) v2[++p] = sa[i] - j;
for (i = 1; i <= len; i++) v1[i] = rnk[v2[i]];
for (i = 1; i <= tot; i++) sum[i] = 0;
for (i = 1; i <= len; i++) sum[v1[i]]++;
for (i = 2; i <= tot; i++) sum[i] += sum[i - 1];
for (i = len; i >= 1; i--) sa[sum[v1[i]]--] = v2[i];
for (swap(rnk, v2), rnk[sa[1]] = 1, i = 2, p = 2; i <= len; i++) {
rnk[sa[i]] = cmp(v2, sa[i - 1], sa[i], j) ? p - 1 : p++;
}
}
}
void calheight() {
ll i, j, p = 0;
for (i = 1; i <= len; i++) {
if (p) p--;
j = sa[rnk[i] - 1];
while (s[i + p] == s[j + p]) p++;
height[rnk[i]] = p;
}
}
ull ksm[150];
int main() {
ksm[0] = 1;
for (int i = 1; i <= 130; i++) {
ksm[i] = ksm[i - 1] * P;
}
scanf("%lld%lld", &n, &m);
for (ll i = 1; i <= n; i++) {
scanf("%s", arr[i] + 1);
for (ll j = 1; j <= m; j++) {
_hash[i][j] = _hash[i][j - 1] * P + arr[i][j] - 'A' + 1;
}
}
for (ll w = 1; w <= m; w++) {
tot = 0, len = 0;
mp.clear();
for (ll j = 1; j + w - 1 <= m; j++) {
for (ll i = 1; i <= n; i++) {
ull tmp = _hash[i][j + w - 1] - _hash[i][j - 1] * ksm[w];
if (mp[tmp] == 0) {
mp[tmp] = ++tot;
}
s[++len] = mp[tmp];
}
s[++len] = ++tot;
}
da();
calheight();
ans += n * (n + 1) / 2 * (m - w + 1);
for (ll i = 2; i <= len; i++) {
ans -= height[i];
}
}
cout << ans;
return 0;
}
随机序列[SHOI2016] [4]
这道题的题意就是给你n个数让你在每个数之间插入+、-、*三种运算符中的一种,然后算出一个答案,再把答案加起来。
这题肯定是不能暴力的(题目都告诉你了由3n-1种结果)。我们先从小的情况枚举找一找规律。
n=1
a1
n=2
2a1+a1a2
n=3
6a1+2a1a2+a1a2*a3
n=4
18a1+6a1a2+2a1a2a3+a1a2a3a4
发现没有?每一项是一个前缀积,每一项的系数除了最后两项都是后一项*3。这样我们就可以拿线段树维护这个答案了。
每次改我们就在[k, n]这个区间a[k]的逆v(除a[k]乘v),在求一下[1, n]的和就是答案了。
别忘了要把a[k]赋成v。
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const ll N = 100010;
const ll mod = 1000000007;
ll n, Q;
ll a[N], mul[N];
struct Segment_Tree{
ll val, tag;
}st[N << 2];
ll ksm(ll x, ll y) {
ll ret = 1;
while (y) {
if (y & 1) ret = (ret * x) % mod;
y >>= 1;
x = (x * x) % mod;
}
return ret;
}
void build(ll x, ll l, ll r) {
st[x].tag = 1;
if (l == r) {
if (l == n) {
st[x].val = mul[n] % mod;
} else if (l == n - 1) {
st[x].val = (2 * mul[n - 1]) % mod;
} else {
st[x].val = (((ksm(3, n - l - 1) * 2) % mod) * mul[l]) % mod;
}
return;
}
ll mid = (l + r) >> 1;
build(x << 1, l, mid);
build(x << 1 | 1, mid + 1, r);
st[x].val = (st[x << 1].val + st[x << 1 | 1].val) % mod;
}
void push_down(ll x) {
if (st[x].tag != 1) {
st[x << 1].tag = (st[x].tag * st[x << 1].tag) % mod;
st[x << 1].val = (st[x].tag * st[x << 1].val) % mod;
st[x << 1 | 1].tag = (st[x].tag * st[x << 1 | 1].tag) % mod;
st[x << 1 | 1].val = (st[x].tag * st[x << 1 | 1].val) % mod;
st[x].tag = 1;
}
}
void change(ll x, ll l, ll r, ll p, ll q, ll v) {
if (r < p || l > q) return;
if (p <= l && r <= q) {
st[x].tag = (st[x].tag * v) % mod;
st[x].val = (st[x].val * v) % mod;;
return;
}
push_down(x);
ll mid = (l + r) >> 1;
change(x << 1, l, mid, p, q, v);
change(x << 1 | 1, mid + 1, r, p, q, v);
st[x].val = (st[x << 1].val + st[x << 1 | 1].val) % mod;
}
ll read() {
ll ret = 0, f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
ret = (ret << 1) + (ret << 3) + ch - '0';
ch = getchar();
}
return ret * f;
}
int main() {
mul[0] = 1;
n = read(), Q = read();
for (ll i = 1; i <= n; i++) {
a[i] = read();
mul[i] = (mul[i - 1] * a[i]) % mod;
}
build(1, 1, n);
while (Q--) {
ll t, v;
t = read(), v = read();
change(1, 1, n, t, n, (ksm(a[t], mod - 2) * v) % mod);
cout << st[1].val << "\n";
a[t] = v;
}
return 0;
}
落谷P1872 回文串计数 [3]
这道题显然可以用PAM做出来。
PAM可以算出以字符串的第ii个字符为结尾的回文子串的个数。我们将其存到一个数组l[n],再求一个前缀和就可以把字符串的前i个字符的前缀有多少个回文子串求出来。
然后,我们将PAM清空,倒着做一遍,就可以求出以第i个字符为左端点的回文子串个数r[i]。与它不相交的回文子串且在它前面的子串有l[i - 1]个,相乘再累加就是答案。
此题在落谷的评级是绿,那是因为此题数据范围只有2000,不用PAM也可以做。但此题可以当做PAM入门的练手题。
#include <iostream>
#include <cstdio>
#include <cstring>
#define ll long long
using namespace std;
const int N = 200000;
struct Plalindromic_Tree{
int go[26], len, fail;
ll fail_len;
}pt[N];
int lst, tot;
char s[N], ss[N];
void build() {
lst = tot = 0;
ss[0] = -1;
pt[++tot].len = -1;
pt[0].fail = pt[1].fail = 1;
pt[0].fail_len = 2;
pt[1].fail_len = 1;
}
int add(int c, int n) {
int p = lst;
ss[n] = c + 'a';
while (ss[n - pt[p].len - 1] != ss[n]) p = pt[p].fail;
if (!pt[p].go[c]) {
int v = ++tot, k = pt[p].fail;
pt[v].len = pt[p].len + 2;
while (ss[n - pt[k].len - 1] != ss[n]) k = pt[k].fail;
pt[v].fail = pt[k].go[c];
pt[v].fail_len = pt[pt[v].fail].fail_len + 1;
pt[p].go[c] = v;
}
return lst = pt[p].go[c];
}
ll r[N], ans;
int lens;
int main() {
scanf("%s", s + 1);
lens = strlen(s + 1);
build();
for (int i = 1; i <= lens; i++) {
r[i] = (pt[add(s[i] - 'a', i)].fail_len - 2) + r[i - 1];
}
memset(pt, 0, sizeof(pt));
build();
for (int i = lens; i > 1; i--) {
ans += (pt[add(s[i] - 'a', lens - i + 1)].fail_len - 2) * r[i - 1];
}
cout << ans;
return 0;
}
LG5838 [USACO19DEC]Milk Visits G [3]
这题是Silver T3的扩展。
有了ST3的提示,我们知道只要确定一条链上某种颜色的个数即可。
显然这是可以在线做的。
看到网上的题解大多是用主席树写的。我就介绍一种用线段树合并的做法,其实思路是一样的。
在每个节点维护一棵线段树,每个叶节点代表从根到此节点的一种颜色的个数。
首先这课线段树肯定是要动态开点的。
对于每个节点,先将它自己的颜色插入它对应的线段树。
for (int i = 1; i <= n; i++) {
cin >> t[i];
add(rt[i], 1, n, t[i]);
}
然后我们递归。每递归到一个节点x,我们就将它父亲的线段树合并到它的线段树(感觉就像主席树换了种写法。。。)
对于每组询问 \((a, b, c)\),我们通过线段树查询\(a\),\(b\) 和 \(lca(a, b)\)可以求出从根分别到它们的路径上 \(c\) 的个数,然后一加一减就可以知道 \(a->b\) 的路径上 \(c\) 的个数。
这道题就做完了。
完整代码:
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 100010;
struct seg_tree{
int val, lson, rson;
}st[N * 100];
int len, rt[N];
struct node{
int pre, to;
}edge[2 * N];
int head[N], tot;
int n, m;
int t[N];
int depth[N], f[N][25];
int lca(int x, int y) {
if (depth[x] < depth[y]) swap(x, y);
int d = depth[x] - depth[y];
for (int i = 0; i <= 20; i++) {
if ((1 << i) & d) {
x = f[x][i];
d -= (1 << i);
}
}
if (x == y) return x;
for (int i = 20; i >= 0; i--) {
if (f[x][i] != f[y][i]) {
x = f[x][i];
y = f[y][i];
}
}
return f[x][0];
}
void ad(int u, int v) {
edge[++tot] = node{head[u], v};
head[u] = tot;
}
void add(int &x, int l, int r, int v) {
if (!x) x = ++len;
if (l == r) {
st[x].val++;
return;
}
int mid = (l + r) >> 1;
if (v <= mid) add(st[x].lson, l, mid, v);
else add(st[x].rson, mid + 1, r, v);
st[x].val = st[st[x].lson].val + st[st[x].rson].val;
}
int merge(int u, int v) {
if (!u) return v;
if (!v) return u;
st[u].val += st[v].val;
st[u].lson = merge(st[u].lson, st[v].lson);
st[u].rson = merge(st[u].rson, st[v].rson);
return u;
}
void dfs(int x, int fa) {
for (int i = 1; i <= 20; i++) {
f[x][i] = f[f[x][i - 1]][i - 1];
}
for (int i = head[x]; i; i = edge[i].pre) {
int y = edge[i].to;
if (y == fa) continue;
f[y][0] = x;
depth[y] = depth[x] + 1;
rt[y] = merge(rt[y], rt[x]);
dfs(y, x);
}
}
int ask(int x, int l, int r, int p) {
if (!x) return 0;
if (l == r) return st[x].val;
int mid = (l + r) >> 1;
if (p <= mid) return ask(st[x].lson, l, mid, p);
else return ask(st[x].rson, mid + 1, r, p);
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> t[i];
add(rt[i], 1, n, t[i]);
}
for (int i = 1, a, b; i < n; i++) {
cin >> a >> b;
ad(a, b);
ad(b, a);
}
dfs(1, 0);
for (int i = 1, a, b, c; i <= m; i++) {
cin >> a >> b >> c;
int LCA = lca(a, b);
if (ask(rt[a], 1, n, c) + ask(rt[b], 1, n, c) - ask(rt[LCA], 1, n, c) - ask(rt[f[LCA][0]], 1, n, c) > 0) cout << 1;
else cout << 0;
}
return 0;
}
单词「TJOI 2013」[3]
我们正常的建好Trie后求一遍fail。之后对于每一个节点,从它的fail连向它一条单项边。然后从根节点开始dfs。
记sum[i]代表从根到i号节点所代表的的字符串出现的次数,即该点的权值。
设当前的节点为x,他有一个孩子y,则使sum[x] += sum[y]。
记得记录一下每个字符串结尾的节点编号,设第i个字符串结尾的编号为id[i],对于每个字符串i最后输出sum[id[i]]即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
int trie[5000010][26], fail[5000010], sum[5000010], tot = 1;
int n;
int end_id[210];
char s[5000010];
queue<int> q;
vector<int> vec[5000010];
void solve(int x) {
for (int i = 0; i < (int)vec[x].size(); i++) {
solve(vec[x][i]);
sum[x] += sum[vec[x][i]];
}
}
int main() {
cin >> n;
for (int i = 1, p, len; i <= n; i++) {
scanf("%s", s + 1);
p = 1;
len = strlen(s + 1);
for (int j = 1; j <= len; j++) {
int k = s[j] - 'a';
sum[p]++;
if (!trie[p][k]) trie[p][k] = ++tot;
p = trie[p][k];
}
sum[p]++;
end_id[i] = p;
}
for (int i = 0; i < 26; i++) trie[0][i] = 1;
fail[1] = 0;
q.push(1);
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = 0; i < 26; i++) {
if (!trie[x][i]) {
trie[x][i] = trie[fail[x]][i];
} else {
vec[trie[fail[x]][i]].push_back(trie[x][i]);
fail[trie[x][i]] = trie[fail[x]][i];
q.push(trie[x][i]);
}
}
}
solve(1);
for (int i = 1; i <= n; i++) {
cout << sum[end_id[i]] << "\n";
}
return 0;
}
CF840D Destiny [3]
和弱化版的思路一样,如果左子树中出现的次数大于要求,则左子树中就可能存在答案,右子树同理否则输出\(-1\)即可。
这里要求最小值所以优先找左子树即可。
这样做的单次查询复杂度是\(O(k \log{n})\)的,\(k\)很小,肯定能过。
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 300010;
struct Segment{
int lson, rson, val;
}tr[N * 30];
int tot;
int n, m;
int a[N], rt[N];
void ins(int &cur, int pre, int l, int r, int pos, int v) {
cur = ++tot;
tr[cur] = tr[pre];
tr[cur].val += v;
if (l == r) return;
int mid = (l + r) >> 1;
if (pos <= mid) ins(tr[cur].lson, tr[pre].lson, l, mid, pos, v);
else ins(tr[cur].rson, tr[pre].rson, mid + 1, r, pos, v);
}
bool ask(int x, int y, int l, int r, int k) {
if (l == r) {
printf("%d\n", l);
return true;
}
int mid = (l + r) >> 1;
if (tr[tr[y].lson].val - tr[tr[x].lson].val > k) {
if (ask(tr[x].lson, tr[y].lson, l, mid, k)) return true;
}
if (tr[tr[y].rson].val - tr[tr[x].rson].val > k) {
if (ask(tr[x].rson, tr[y].rson, mid + 1, r, k)) return true;
}
return false;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
ins(rt[i], rt[i - 1], 1, n, a[i], 1);
}
while (m--) {
int l, r, k;
scanf("%d%d%d", &l, &r, &k);
k = (r - l + 1) / k;
if (!ask(rt[l - 1], rt[r], 1, n, k)) puts("-1");
}
return 0;
}
LG1613 跑路 [3]
题意
小A的工作不仅繁琐,更有苛刻的规定,要求小A每天早上在6:00之前到达公司,否则这个月工资清零。可是小A偏偏又有赖床的坏毛病。于是为了保住自己的工资,小A买了一个十分牛B的空间跑路器,每秒钟可以跑2^k千米(k是任意自然数)。当然,这个机器是用longint存的,所以总跑路长度不能超过maxlongint千米。小A的家到公司的路可以看做一个有向图,小A家为点1,公司为点n,每条边长度均为一千米。小A想每天能醒地尽量晚,所以让你帮他算算,他最少需要几秒才能到公司。数据保证1到n至少有一条路径。
题解
这道最毒瘤的地方就是给人错觉求一遍最短路即可。
其实样例就已经在提醒你了(然而我用错误的方法还是直接过了样例并且拿到了40分)。
步入正题
显然如果两个点之间有一条长度为\(2^k\)的路的话它们之间的距离就是1。
根据这一点可以设计一个状态: \(dp[i][j][k]\)待表i,j之间是否有一条长度为\(2^k\)。
初始化若有u->v的一条边,则dp[u][v][0]=1
有了子状态很容易想到转移方程,找到一个中介点l,判断dp[i][l][k-1],dp[l][j][k-1]是否都成立。
注意循环的顺序,k应该在最外层循环。
然后我们再根据上面得到的结果,建一个新图,跑最短路即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
const int M = 10010;
const int N = 60;
struct node{
int pre, to;
}edge[M << 1];
int head[N], tot;
int n, m;
int dis[N][N];
bool f[N][N][64];//f[i][j][k]代表i到j能否跑出长为2^k这样的路径
void add(int u, int v) {
edge[++tot] = node{head[u], v};
head[u] = tot;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, u, v; i <= m; i++) {
scanf("%d%d", &u,&v);
add(u, v);
f[u][v][0] = 1;
}
for (int k = 0; k <= 63; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int l = 1; l <= n; l++) {
f[i][j][k] |= f[i][l][k - 1] && f[l][j][k - 1];
}
}
}
}
memset(dis, 0x3f, sizeof(dis));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 0; k <= 63; k++) {
if (f[i][j][k]) {
dis[i][j] = 1;
}
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}
printf("%d", dis[1][n]);
return 0;
}
罗马游戏[2]
左偏树模板题。
只不过这里要加上并查集的路径压缩(因为要找堆顶),不然复杂度是错的。
因为一个人被杀了,他就没了,为了证明他没了,所以要把他的val设成-1。
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 1000010;
struct Leftist_Tree{
int lson, rson, val, dist, fa;
}t[N];
int merge(int x, int y) {
if (!x || !y) return x | y;
if (t[x].val > t[y].val) {
swap(x, y);
}
t[x].rson = merge(t[x].rson, y);
if (t[t[x].rson].dist > t[t[x].lson].dist) {
swap(t[x].lson, t[x].rson);
}
t[t[x].lson].fa = t[t[x].rson].fa = t[x].fa = x;
t[x].dist = t[x].dist + 1;
return x;
}
int get(int x) {
return t[x].fa == x ? x : t[x].fa = get(t[x].fa);//路径压缩
}
void pop(int x) {
t[x].val = -1;
t[t[x].lson].fa = t[x].lson;
t[t[x].rson].fa = t[x].rson;
t[x].fa = merge(t[x].lson, t[x].rson);
}
int n, m, a[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
t[i].fa = i;
t[i].val = a[i];
}
scanf("%d", &m);
while (m--) {
char opt[5];
int x, y;
scanf("%s%d", opt + 1, &x);
if (opt[1] == 'M') {
scanf("%d", &y);
if (t[x].val == -1 || t[y].val == -1) continue;
if (get(x) == get(y)) continue;
t[get(x)].fa = t[get(y)].fa = merge(get(x), get(y));
} else {
if (t[x].val == -1) puts("0");
else printf("%d\n", t[get(x)].val), pop(get(x));
}
}
return 0;
}

