基于ROM的位分解4位二进制数乘法器设计

1 设计要求

　　设计一个4位二进制数乘法器，采用查找表实现（这里将高位宽的数据分解成低位宽的数据再调用查找表乘法器）。

2 设计分析

2.1 架构设计

　　4位乘法器的框图如下图所示。其中，clk为系统时钟，rst_n系统复位，低电平有效，a[3:0]为被乘数，b[3:0]为乘数，out[7:0]为积。

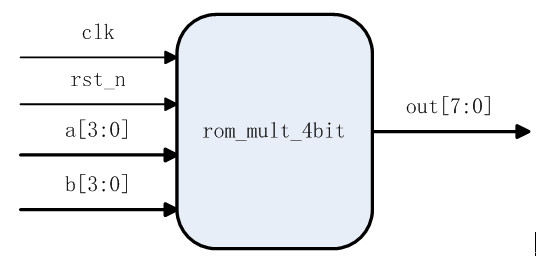
2.2 原理分析

（1）ROM原理

       乘法器的一种实现思想是采用ROM的方式，即将被乘数和乘数连接起来拼成地址，把两者所有可能的乘积按照地址号存放在ROM的地址空间中，两个数相乘时，根据两者构成的地址从ROM索取乘积结果。

       如两个1bit的数相乘，可能的相乘方式有0x1,0x0,1x1,1x0,一共四种相乘方式，其对应的结果也有四种,即0,0,1,0。那么如果将这四个结果存在ROM中，其实正好用01,00,11,10四个地址来寻址。因此是可以把所有的乘积结果都包含在内的。

       通俗的来说，两个Nbit二进制数相乘，其结果为2Nbit，这意味着ROM的深度为2^(2N),宽度为（2N）,占用的空间大小为2^(2N)x2N。以两个4bit 的数相乘例子，其存储空间大小为256x8bit。显然随着位宽的增长，存贮空间将以指数速度膨胀，这是这个方法的一个弊端。

（2）位分解原理

       由于上述弊端的存在 ，一种改进方法就是进行位分解，将两个大位宽的数相乘分解为多个小位宽的数相乘。例如，设 A,B 为两个 8 位数据，可将 A 分解为 A=A1×16+A2，其中 A1 为高 4 位，A2 为低 4 位；同理 B=B1×16+B2，然后A×B=(A1×16+A2)×(B1×16+B2)=A1*B1*16*16 + A1*B2*16 + A2*B1*16 + A2*B2（此处可以用左移来表示）。这样就将两个 8 位数的相乘转化为 4 组 4 位数相乘，然后再相加，其中乘以常数可以通过移位运算实现，大大地缩减了存储空间，其硬件结构如下图所示：

（3）4位二进制数乘法器

根据公式   A=A1×2^N+A2 可得知 N=2；最后得到式子：

 A*B=(A1*4+A2)*(B1*4+B2)=A1*B1*4*4+A1*B2*4+A2*B1*4+A2*B3

A[3：0]×B[3：0] = A[3：2]×B[3：2]+ A[1：0]×B[3：2] +

A[3：2]×B[1：0] + A[1：0]×B[1：0] = (outa *16) + (outb *4)+ (outc *4) + outd= (outa << 4) + (outb << 2) + (outc << 2) + outd;

2.3 架构设计

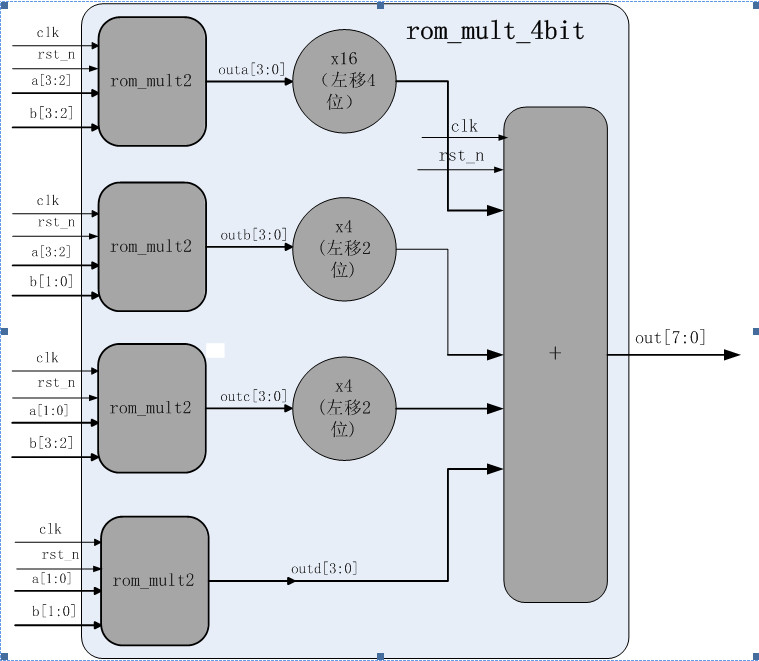
3 设计实现

3.1 顶层设计

module rom_mult_4bit(
    input     wire                 clk,
    input     wire                 rst_n,
    input     wire     [3:0]        a,
    input     wire     [3:0]        b,
    
    output     reg     [7:0]        out
);
    
    wire         [3:0]            outa;
    wire         [3:0]            outb;
    wire         [3:0]            outc;
    wire         [3:0]            outd;
    
    rom_mult_2bit rom_mult_2bit0(
            .clk                    (clk),
            .rst_n                (rst_n),
            .a                        (a[3:2]),
            .b                        (b[3:2]),
            .out                    (outa)
        );
    
    rom_mult_2bit rom_mult_2bit1(
            .clk                    (clk),
            .rst_n                (rst_n),
            .a                        (a[3:2]),
            .b                        (b[1:0]),
            .out                    (outb)
        );
    
    rom_mult_2bit rom_mult_2bit2(
            .clk                    (clk),
            .rst_n                (rst_n),
            .a                        (a[1:0]),
            .b                        (b[3:2]),
            .out                    (outc)
        );
    
    rom_mult_2bit rom_mult_2bit3(
            .clk                    (clk),
            .rst_n                (rst_n),
            .a                        (a[1:0]),
            .b                        (b[1:0]),
            .out                    (outd)
        );
    
    always@(posedge clk or negedge rst_n)begin
        if(rst_n == 1'b0)
            out <= 8'd0;
        else
            out <= (outa << 4) + (outb << 2) + (outc << 2) + outd;
    end    

endmodule 

3.2 基于rom的2位乘法器设计

module rom_mult_2bit(
    input     wire                 clk,
    input     wire                 rst_n,
    input     wire     [1:0]        a,
    input     wire     [1:0]        b,
    
    output     reg     [3:0]        out
);

    always@(posedge clk or negedge rst_n)begin
        if(rst_n == 1'b0)
            out <= 4'd0;
        else begin
            case({a,b})
                4'b0000    :     out <= 4'd0;
                4'b0001    :     out <= 4'd0;
                4'b0010    :     out <= 4'd0;
                4'b0011    :     out <= 4'd0;
                
                4'b0100    :     out <= 4'd0;
                4'b0101    :     out <= 4'd1;
                4'b0110    :     out <= 4'd2;
                4'b0111    :     out <= 4'd3;
                
                4'b1000    :     out <= 4'd0;
                4'b1001    :     out <= 4'd2;
                4'b1010    :     out <= 4'd4;
                4'b1011    :     out <= 4'd6;
                
                4'b1100    :     out <= 4'd0;
                4'b1101    :     out <= 4'd3;
                4'b1110    :     out <= 4'd6;
                4'b1111    :     out <= 4'd9;
                default    : out <= 4'd0;
            endcase
        end
    end
    
endmodule 

4 仿真验证

`timescale 1ns/1ps

module rom_mult_4bit_tb();

    reg                         clk;
    reg                        rst_n;
    reg         [3:0]            a;
    reg         [3:0]            b;
    
    wire         [7:0]            out;
    
    wire         [7:0]            tb_out;
    reg         [7:0]            tb_out_r;
    reg       [7:0]            tb_out_rr;
    
    assign tb_out = a * b;
    
    always@(posedge clk)begin
        tb_out_r     <= tb_out;
        tb_out_rr    <= tb_out_r;
    end
    
    rom_mult_4bit rom_mult_4bit_inst(
        .clk                    (clk),
        .rst_n                (rst_n),
        .a                        (a),
        .b                        (b),
    
        .out                    (out)
    );

    initial clk = 1'b0;
    always #10 clk = ~clk;
    
    initial begin
        rst_n = 1'b0; a = 4'd0; b = 4'd0;
        #21; rst_n = 1'b1;
        #20;
        repeat(10)begin
            a = {$random}%16;
            b = {$random}%16;
            #20;
        end
        #50;
        $stop;
    end
    
endmodule 

5 参考文献：
（1）(49条消息) 乘法器设计(二)：基于ROM的乘法器设计_MaoChuangAn的博客-CSDN博客；