基于FPGA的4位二进制数除法器设计

1. 设计要求：

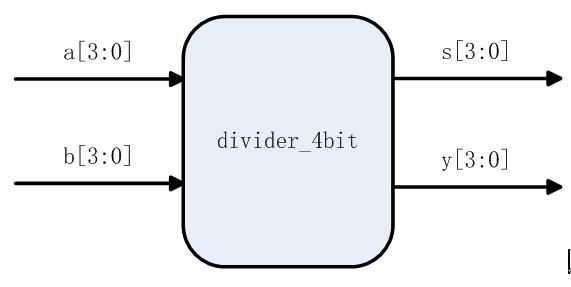
　　设计一个4位二进制数除法器，如下图所示。其中，a[3:0]为被除数，b[3:0]为除数，s[3:0]为商，r[3:0]为余数。

2. 设计原理：

　　和十进制除法类似，以计算 27 除以 5 的过程为例：除法运算过程如下：

(1) 取被除数的高几位数据，位宽和除数相同（实例中是 3bit 数据）。

(2) 将被除数高位数据与除数作比较，如果前者不小于后者，则可得到对应位的商为 1，两者做差得到第一步的余数；否则得到对应的商为 0，将前者直接作为余数。

(3) 将上一步中的余数与被除数剩余最高位 1bit 数据拼接成新的数据，然后再和除数做比较。可以得到新的商和余数。

(4) 重复过程 (3)，直到被除数最低位数据也参与计算。

需要说明的是，商的位宽应该与被除数保持一致，因为除数有可能为1。所以上述手动计算除法的实例中，第一步做比较时，应该取数字 27 最高位 1 (3’b001) 与 3’b101 做比较。 根据此计算过程，设计位宽可配置的流水线式除法器，流水延迟周期个数与被除数位宽一致。

3. 设计实现

module divider_4bit(
    
    input　　　　wire        [3:0]            a,
    input　　　　wire         [3:0]            b
    
    output　　　　wire         [3:0]            s,
    output　　　　wire        [3:0]            y
);


    wire                    [3:0]            part_0;
    wire                    [3:0]            part_1;
    wire                    [3:0]            part_2;
    wire                    [3:0]            part_3;
    
    assign s[3] = a[3] >= b;                                        //最高位的商s[3]
    assign part_3 = (s[3] == 1'b1 )? a[3] - b : a[3];        
    
    assign s[2] = {part_3, a[2]} >= b;
    assign part_2 = (s[2] == 1'b1) ? {part_3, a[2]} - b : {part_3, a[2]};
    
    assign s[1] = {part_2, a[1]} >= b;
    assign part_1 = (s[1] == 1'b1) ? {part_2, a[1]} - b : {part_2, a[1]};
    
    assign s[0] = {part_1, a[0]} >= b;
    assign part_0 = (s[0] == 1'b1) ? {part_1, a[0]} - b : {part_1, a[0]};
    
    assign y = part_0;

endmodule 

4. 仿真验证

`timescale 1ns/1ps
module divider_4bit_tb();
      
    reg        [3:0]            a;
    reg        [3:0]            b; 
    wire        [3:0]            s;
    wire        [3:0]            y;
    
    wire        [3:0]            tb_s;
    wire        [3:0]            tb_y;
    
    assign tb_s = a / b;
    assign tb_y = a % b;

    divider_4bit divider_4bit_inst (    
        .a                (a),
        .b                (b),        
        .s                (s),
        .y                (y)
    );

   initial begin
        repeat(20)begin
            a = {$random} % 16;
            b = {$random} % 16;
            # 20;
        end    
    end

endmodule 

 

注：0/0=无穷大，任何数除以零（无穷小）得无穷大，而在Veriog中，默认0/0=错误结果，s[3:0]最大值为15。