基于FPGA的4位二进制数乘法器设计

1. 设计要求：

设计一个4位二进制数乘法器，如下图所示。其中，a[3:0]为被乘数，b[3:0]为乘数，m[7:0]为积，即乘法结果。

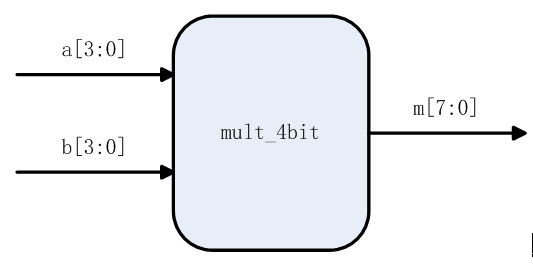
注意：为什么乘法结果的有效位数要定义为8位？如：15x15=225。一般情况下，乘法结果的有效位数应为两个乘数位宽之和，从而保证得到正确的结果。

2. 设计原理

       由于被乘数和乘数都是二进制，利用人工计算来分析（移位相加方法），所以利用乘数从第一位到最后一位每一位依次与被乘数相乘，从第二位开始每一位都要依次左移一位，形成一个阵列的式。而由于两个一位二进制数相乘，实际上是做与运算，所以就将乘法操作简化为了与运算、移位操作以及加法操作。比如 1011与 1101相 乘，如图，实际上可看作 1011+00000+101100+1011000四个数相加。

 

 

 

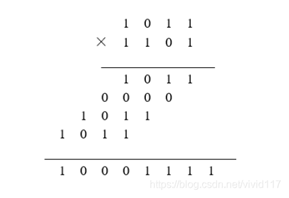
 3. 设计实现

module mult_4bit(
    input    　　wire    [3:0]        a,
    input       wire    [3:0]        b,
    output    　wire    [7:0]        m
);
    
    wire                [7:0]        part_0;
    wire                [7:0]        part_1;
    wire                [7:0]        part_2;
    wire                [7:0]        part_3;
    
    assign part_0 = {4'd0, a & {4{b[0]}}};
    assign part_1 = {3'd0, a & {4{b[1]}}, 1'd0};
    assign part_2 = {2'd0, a & {4{b[2]}}, 2'd0};
    assign part_3 = {1'd0, a & {4{b[3]}}, 3'd0};
    
    assign m = part_0 + part_1 + part_2 + part_3;
    
endmodule

4. 仿真验证

`timescale 1ns/1ps

module mult_4bit_tb();

    reg         [3:0]        a;
    reg         [3:0]        b;
    wire        [7:0]        m;
    
    wire         [7:0]        tb_m;
    
    assign tb_m = a * b;
    
    mult_4bit mult_4bit_inst(
        .a                (a),
        .b                (b),
        .m                (m)
    );
    
    initial begin
        repeat(10)begin
            a = {$random}%16;
            b = {$random}%16;
            #20;
        end
    end
    
endmodule

功能仿真（不考虑延时）

注意：乘法器所消耗的资源和运行速度与所用FPGA具体型号等因素有关。