全体自然数的和是负十二分之一?
“全体自然数的和是-1/12”这个惊人的结论已经在互联网上传播了许多年,那么,全体自然数的和是-1/12,这是怎么来的?
一个最通俗,所以也最引人争议的做法,是一种看上去很简单的算术算法:
首先令S0=1-2+3-4+5-6……
我们在大学里的学过令它收敛到1/4的方法。
再令全体自然数的和为S,减去这个S0,则有:
S-S0=0+4+0+8+0+12+0+16+……
=4*(1+2+3+4+....)=4S
也就是说-S0等于3个S,所以S等于负十二分之一。
还有个误解在黎曼ζ(zeta)函数的解析延拓有
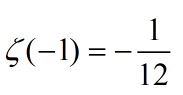
得到了印证,让很多人深信不疑。
下面我们探讨一下S0和 S到底存不存在:
柯西和(就是高数书上的定义)
级数收敛的必要条件是一般项的极限是0
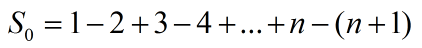
的一般项是
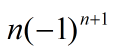
其极限不是0,所以 S0 不收敛.

的一般项是n ,其极限不是0,所以 S不收敛
Cesaro和
在此之前有必要了解一下Cesaro和的定义,它是部分和的平均,也就是
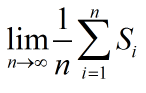
在Cesaro和的意义下, S0还是不收敛的。
这是因为 奇数项是
,偶数项是0 ,故
这个极限根本不存在,也即S0 没有Cesaro和。
广义Cesaro和
那么,我们再拓展一下,既然一次平均不行,我们取部分和平均的平均,如何?
这就是广义Cesaro和。
很幸运的是,这时候S0 终于可以求和了,它在广义Cesaro和的意义下是 1/4
Ramanujan和(拉马努金和)
Ramanujan断言,对于函数 ,定义新的和作为Ramanujan和:
小结
S0没有柯西和,没有Cesaro和,有广义Cesaro和,有Ramanujan和
S没有柯西和,没有Cesaro和,没有广义Cesaro和,有Ramanujan和
严格来说,Rmanujan和,已经改变了原来“和”的定义。简单来说,不满足结合律
举个例子:
假设
那么
因此,
显然,不成立
再看下再黎曼ζ函数下的误解:
由于黎曼ζ函数原本的定义是
(其中s为复数),
如果把s取为-1的话,等号右边就变成了1+2+3+...这样的“全体自然数之和”,似乎
就自然推出了“全体自然数之和等于负十二分之一”。但是要注意,原始的黎曼ζ函数是定义在s的实部大于1的区间中的,也就是说原始的ζ(s)在s=-1时根本没有意义。
那么这个是怎么回事呢?这里就需要介绍“解析延拓”这个概念。
假设两个函数分别在两个区域中解析,而这两个区域有公共部分,在公共部分上两个函数相等,那么就可以把这两个函数在两个区域的并集上的全体点的数值集,看成一个在两区域的并集上解析的新函数,此时这两个函数就是彼此的解析延拓。具体的例子可以去百度。重点就是,  是在黎曼ζ函数解析延拓后得到的结果,可以认为此时的ζ(s)含义已经与之前不同,也自然不能将负十二分之一看成“全体自然数之和”
是在黎曼ζ函数解析延拓后得到的结果,可以认为此时的ζ(s)含义已经与之前不同,也自然不能将负十二分之一看成“全体自然数之和”



