隐马尔可夫模型(二)维特比算法
接着上篇
隐马尔可夫模型
隐马尔可夫的三个问题,上文提了问题1的三种解决办法,本文接着讲问题2
问题2,即在给出一串观测序列的情况下和已知HMM模型的情况下,找到最可能的隐性状态序列
问题2的解决:
维特比算法
1 简介
维特比算法是一个特殊但应用最广的动态规划算法,它是针对最短路径问题而提出的。凡是使用隐含马尔可夫模型描述的问题都可以用维特比算法来解码,包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。
2 示例
下面举一个比较简单的例子做说明:求S到E的最短路径。如下图(各点之间距离不相同):

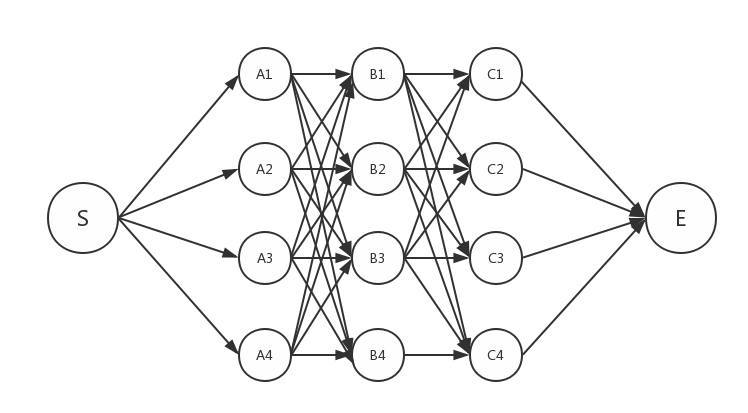
因此,这里选择使用一种基于动态规划的方式来寻找最佳路径。
所谓动态规划。其核心就是“动态”的概念,把大的问题细分为多个小的问题,基于每一步的结果再去寻找下一步的策略,通过每一步走过之后的局部最优去寻找全局最优。这样解释比较抽象,下面直接用回刚刚的例子说明。如下图:

同理,我们也可以得出从S到B2点为两点间最短子路径的结论。
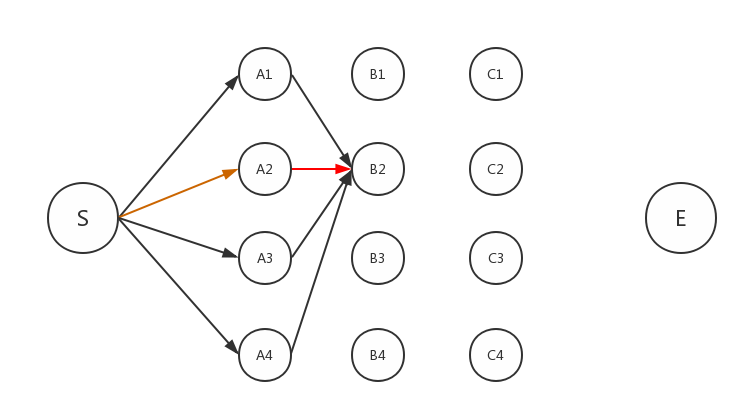

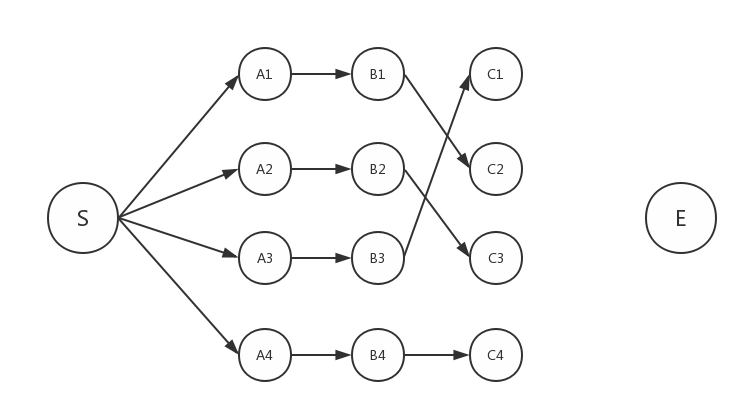
回顾之前的分析:我们计算从S起到C2点的最短路径时候只需要考虑从S出发到B层所有节点的最短路径,B层也如是。对B2来说,一共有4条路线可以到达,分别是A1→B2,A2→B2,A3→B2,A4→B2。我们需要做的就是把A2→B2这条最短路线保留,而其他3条删除掉(因为根据以上的分析,它们不可能构成全程的最短路线)。OK,来到这里,我们会发现一个小“漏洞”,这段S→A2→B2→C2→E的路线只是我一厢情愿的假设,最短路径不一定是经过以上这些点。所以,我们要把每层的每个节点都考虑进来。
以下是具体的做法:
step1:从点S出发。对于第一层的3个节点,算出它们的距离d(S,A1),d(S,A2),d(S,A3),d(S,A4),因为只有一步,所以这些距离都是S到它们各自的最短距离。
step2:对于B层的所有节点(B1,B2,B3,B4),要计算出S到它们的最短距离。我们知道,对于特定的节点B2,从S到它的路径可以经过A层的任何一个节点(A1,A2,A3,A4)。对应的路径长就是d(S,B2)=d(S,Ai)+d(Ai,B2)(其中i=1,2,3,4)。由于A层有4个节点(即i有4个取值),我们要一一计算,然后找到最小值。这样,对于B层的每个节点,都需要进行4次运算,而B层有4个节点,所以共有4X4=16次运算。
step3:这一步是该算法的核心。我们从step2计算得出的结果只保留4个最短路径值(每个节点保留一个)。那么,若从B层走向C层来说,该步骤的基数已经不再是4X4,而是变成了4!也就是说,从B层到C层的最短路径只需要基于B层得出的4个结果来计算。这种方法一直持续到最后一个状态,每一步计算的复杂度为相邻两层的计算复杂度为4X4乘积的正比!再通俗点说,连接这两两相邻层的计算符合变成了“+”号,取代了原先的“X”号。用这种方法,只需进行4X4X2=32次计算!
这就是维特比算法



