友谊悖论
平均来说,一个人的朋友数量往往比他朋友的朋友数量要少。
举个简单的例子:下图中连线的人彼此是朋友,A,B,C,D分别有1,3,2,2个朋友,平均有2个朋友,而我们再看每个人朋友的朋友。A的朋友有3个朋友(来自B),B的朋友分别有1个(A),2个(C),2个(D)朋友,C的朋友分别有3个(B),2个(D)朋友,D的朋友分别有3个(B),2个(C)朋友。平均来说,每个人的朋友有18/8=2.25个朋友
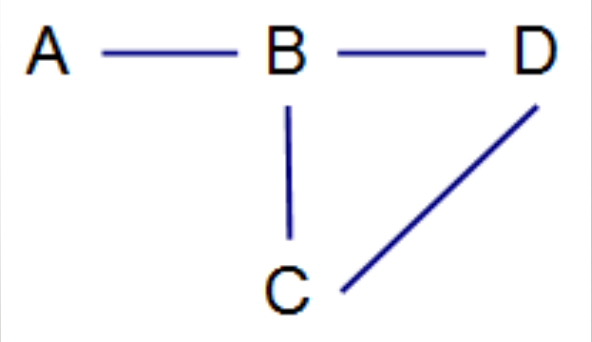
下面是数学解释:
我们用x_ij=1表示i和j是朋友,x_ij=0表示i和j不是朋友,那么我们首先可以意识到j的朋友数量可以表示为:
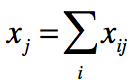
而一个人朋友的朋友总数量可以表示为:
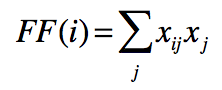
那么一个人的朋友平均拥有的朋友数量就是上面两式相除了,我们将每个人的平均朋友数量和所有人的平均朋友数量就分别表示为:

其中第二个式子相当于把左右的i的mu(i)相加了,也就是我们在例子中如何得到的18/8。那么这个式子分子分母同时除以总人数得到的东西就很简单了:就是一个变量x_i的二阶矩除以一阶矩嘛!我们知道一个变量的方差是二阶矩减去一阶矩的平方,并且方差非负。我们假设x_i的期望是mu_F,标准差是sigma,那么可以得到
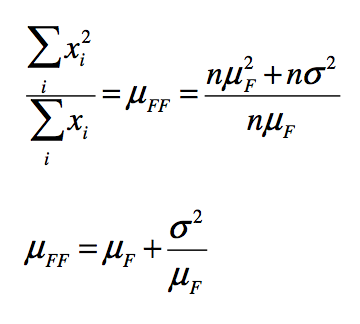
因为方差(sigma的平方)大于0(实际上当所有人都有相同数量的朋友时会取等号,但是现实中几乎没有可能),所以朋友的平均朋友数量是严格大于一个人的平均朋友数量的
如果不用数学解释的话,这是因为那些有很多朋友的人,在计算朋友的朋友数量时会被更多次地被记到,因此会抬高平均数。
尽管粗看起来这个结论有些奇怪,但是仔细一想你就能明白这里面其实就是样本选择偏差的问题
如果你有700个人人好友,你的好友更有可能是只有一两个好友的用户呢,还是更有可能是有着3000好友的用户呢?显然后者更有可能出现在的你好友列表上,既然大家都更有可能结交更“交际花”的用户而不太可能结交没有朋友的用户,那么上述结论也就不难理解了。
“友谊悖论”不仅告诉我们,我们其实比我们的朋友更有可能不受欢迎(其实就算不说我也知道),而且指出了这样一个事实:如果有什么特性是和热门程度或者说曝光度是正相关的,那么我们对拥有这种特性的人群占整个人群的比例的判断很有可能会因为“友谊悖论”而被放大。
这同样可以用来部分解释很多“刻板印象”的存在,注意到很多刻板印象实际上是很不常见的,因而制造这种不常见现象的个体将会被更多人注意:显然不可能所有广东人都是“什么都吃”,但是因为有个别什么都吃的广东人,而这些人又比其它广东人更加“瞩目”,因而对于不熟悉广东的人来说,就会有“广东人都是什么都吃”的错觉了。
再比如一个老生常谈的问题,为什么飞机的失事率命名比火车要低得多,平均里程死亡人数也少得多(这个没查证),人们还是觉得飞机要比火车危险呢?如果你回想一下最近新闻里出现的火车出事事故和飞机出事事故,你就会发现,因为飞机一旦出事,通常都会有各种连篇累牍的报道,而火车事故有这样大仗势的,我一时半会儿也就只想到了温州动车事件。单从这个角度,就会让人们做出飞机比火车危险的判断。



