分布式理论基础(二)选举、多数派和租约
1 选举
1.1 简述
一致性问题(consistency)是独立的节点间如何达成决议的问题,选出大家都认可的leader本质上也是一致性问题,因而如何应对宕机恢复、网络分化等在leader选举中也需要考量。
1.2 Bully算法
Bully算法是最常见的选举算法,其要求每个节点对应一个序号,序号最高的节点为leader。leader宕机后次高序号的节点被重选为leader,过程如下:
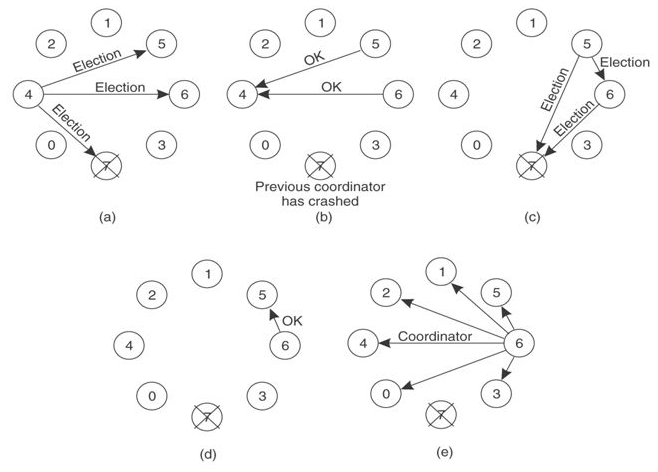
- 节点4发现leader不可达,向序号比自己高的节点发起重新选举,重新选举消息中带上自己的序号
- 节点5、6接收到重选信息后进行序号比较,发现自身的序号更大,向节点4返回OK消息并各自向更高序号节点发起重新选举
- 节点5收到节点6的OK消息,而节点6经过超时时间后收不到更高序号节点的OK消息,则认为自己是leader
- 节点6把自己成为leader的信息广播到所有节点
回顾 分布式理论基础(一)一致性及解决一致性的两种方式:2PC和3PC 就可以看到,Bully算法中有2PC的身影,都具有提议(propose)和收集反馈(vote)的过程。
2 多数派
在网络分化的场景下以上Bully算法会遇到一个问题,被分隔的节点都认为自己具有最大的序号、将产生多个leader,这时候就需要引入多数派(quorum)。多数派的思路在分布式系统中很常见,其确保网络分化情况下决议唯一。
多数派的原理说起来很简单,假如节点总数为2f+1,则一项决议得到多于 f 节点赞成则获得通过。leader选举中,网络分化场景下只有具备多数派节点的部分才可能选出leader,这避免了多leader的产生。
3 租约
选举中很重要的一个问题,以上尚未提到:怎么判断leader不可用、什么时候应该发起重新选举?最先可能想到会通过心跳判别leader状态是否正常,但在网络拥塞或瞬断的情况下,这容易导致出现双主。
租约(lease)是解决该问题的常用方法,其最初提出时用于解决分布式缓存一致性问题,后面在分布式锁等很多方面都有应用。
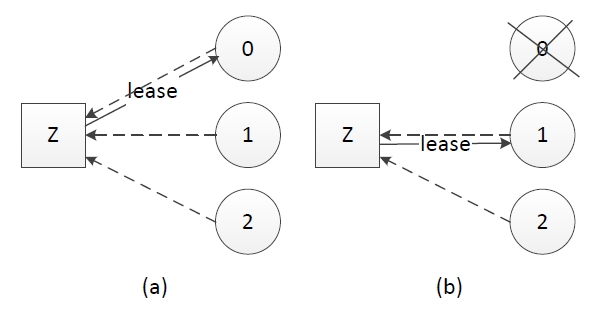
租约的原理同样不复杂,中心思想是每次租约时长内只有一个节点获得租约、到期后必须重新颁发租约。假设我们有租约颁发节点Z,节点0、1和2竞选leader,租约过程如下:
(a) 节点0、1、2在Z上注册自己,Z根据一定的规则(例如先到先得)颁发租约给节点,该租约同时对应一个有效时长;这里假设节点0获得租约、成为leader
(b) leader宕机时,只有租约到期(timeout)后才重新发起选举,这里节点1获得租约、成为leader
租约机制确保了一个时刻最多只有一个leader,避免只使用心跳机制产生双主的问题。在实践应用中,zookeeper等可用于租约颁发。



