机器学习中的Bias、Variance、Error
参考:https://blog.csdn.net/mingtian715/article/details/53789487
https://yoferzhang.gitbooks.io/machinelearningstudy/content/20170327ML03BiasAndVariance.html
https://www.cnblogs.com/sddai/p/9240293.html
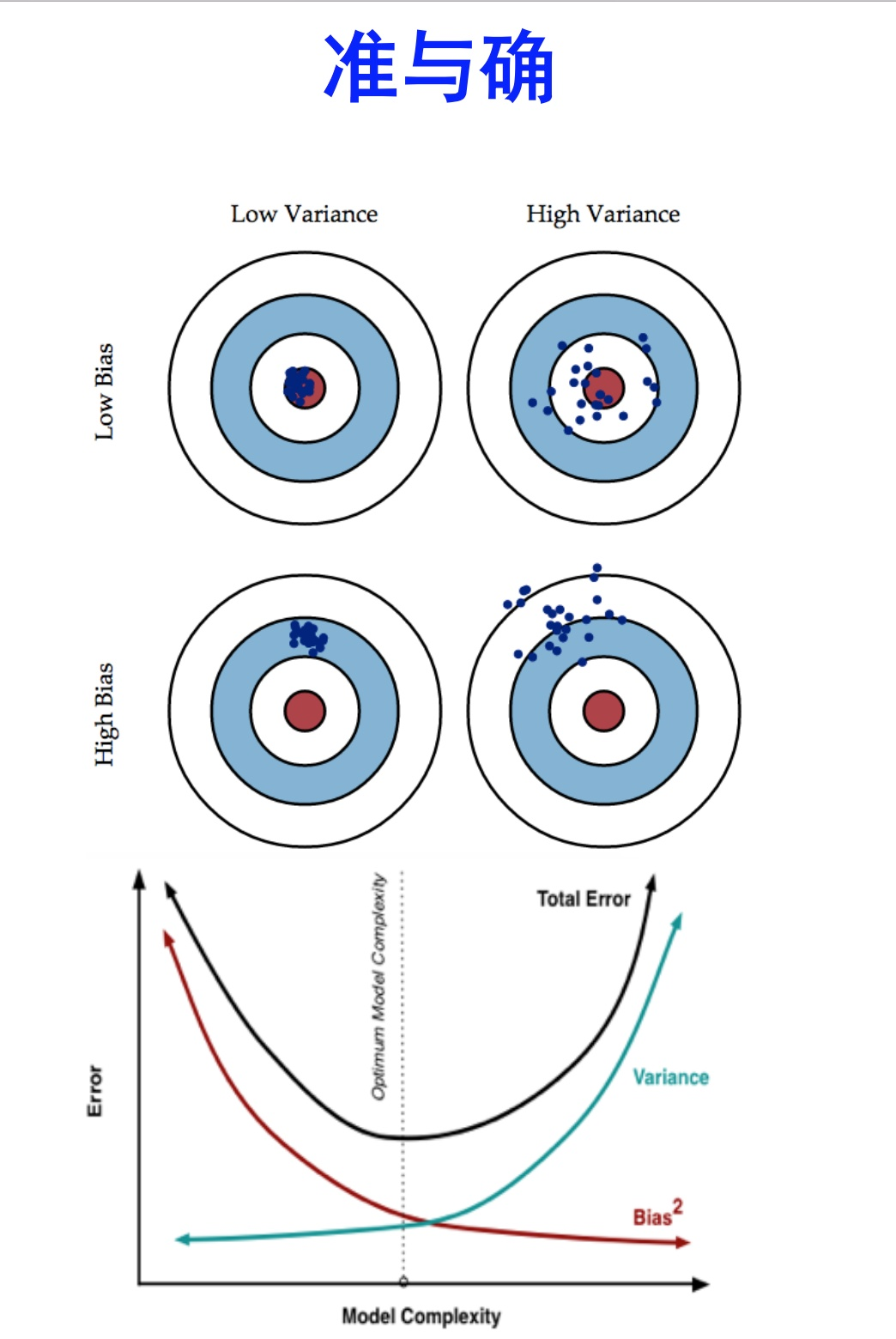
bias描述的是根据样本 拟合出的模型 的输出预测结果的期望 与样本真实结果的 差距,反映的是模型在样本上的输出与真实值之间的误差(经训练出来的模型在测试数据上的拟合程度),即模型本身的精准度。想要得到 low bias,则需要使模型更加复杂(模型越复杂,拟合得就越好),但这容易出现过拟合(注意overfitting),即产生high variance(点分散)。variance描述的是在训练集上训练出来的模型在测试集上的表现,反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。想要得到 low variance就需要简化模型(模型越简单,就越集中),但这容易造成欠拟合,即high bias(注意underfitting)。简单说,方差(variance)描述的是离散,分散程度。偏差(bias)描述的是偏离目标值的程度。Error反映的是整个模型的准确度。
bias表示预测值的均值与真实值之间的差异;而variance表示预测结果作为一个随机变量时的方差。方差是多个模型间的比较,而非针对一个模型而言;偏差可以是单个数据集中的,也可以是多个数据集中的。
我们训练出一个模型的最终目的,是为了让这个模型在测试数据上拟合得不错,也就是error(test)比较小,但在实际问题中,test data我们是拿不到的,也根本不知道test data的内在规律(如果知道了,还machine learning个啥 ),所以我们通过什么策略来减小error(test)呢?
分两步:
让error(train)尽可能小 ;
让error(train)尽可能等于error(test)
三段论,因为A小,而且A=B,这样B就小。
那么怎么让error(train)尽可能小呢?--->> 把模型复杂化,把参数搞得多多的,这个好理解,十元线性回归的error肯定要比二元线性回归的error低。---->> low bias
然后怎么让error(train)尽可能等于error(test)呢?--->> 把模型简单化,把参数搞得少少的。什么叫error(train) = error(test)?就是模型没有偏见,对train,test一视同仁。那么怎样的模型更容易有这这种一视同仁的特性,换句话说,更有通用性(泛化能力),对局部数据不敏感?那就是简单的模型。---->> low variance
解决bias与variance方法
- 在训练集上,进行交叉验证(Cross-Validation):有一种方法叫做K-fold Cross Validation (K折交叉验证), 初始将训练集采样分割成K个子集,一个单独的子集被保留作为验证模型的数据集,其他K-1个子集用来训练模型。交叉验证重复K次,每个子集验证一次,平均K次的结果或者使用其它结合方式,最终得到一个单一估测结果。当K值较大的时候,我们会得到偏小的Bias(偏差), 偏大的Variance;当K值较小的时候,我们会得到偏大的Bias(偏差), 偏小的Variance。cross-validation一大好处是避免了对测试集的二次overfitting。k-fold中的k=5,10比较常见,当然也可以根据你的需要(看样本量怎么可以被整除之类),也要看电脑和软件的运算能力。
- Boosting通过样本变权全部参与,故Boosting 主要是降低 bias(同时也有降低 variance 的作用,但以降低 bias为主);而 Bagging 通过样本随机抽样,抽取出部分样本(单个学习器训练),故bagging主要是降低 variance。
打靶: 真实目标 模型期望 实际结果





