返回一个二维整数数组中最大联通子数组的和
2015年6月22日
1.题目
输入一个二维整形数组,数组里有正数也有负数。
二维数组首尾相接,象个一条首尾相接带子一样。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。
2.设计思路
参照环状一维数组,将二维数组进行扩展。只将数组的列数扩大为原来的2*n-1,行数不变。
3.源代码
#include <iostream>
#include<time.h>
using namespace std;
#define max(a,b) ((a)>(b)?(a):(b))
#define MAXN 100
int A[MAXN][MAXN];
int PartSum[MAXN][MAXN];
//计算子矩阵的和
int MatrixSum(int s, int t, int i, int j)
{
return PartSum[i][j] - PartSum[i][t - 1] - PartSum[s - 1][j] + PartSum[s - 1][t - 1];
}
int main()
{
srand((unsigned)time(NULL));
int row, col, i, j;
cout << "请输入二维数组的行数和列数:";
cin >> row >> col;
for (i = 1; i <= row; i++)
{
for (j = 1; j <= 2 * col - 1; j++)
{
for (j = 1; j <=col; j++)
{
A[i][j] = rand() % 20 - 10;
cout << A[i][j] << " ";
}
for (j = col+1; j <= 2 * col - 1; j++)
{
A[i][j] = A[i][j - col];
//cout << A[i][j] << " ";
}
//cout << A[i][j] << " ";
}
cout<<endl;
}
for (i = 0; i <= row; i++)
PartSum[i][0] = 0;
for (j = 0; j <=2* col-1; j++)
PartSum[0][j] = 0;
// 计算矩阵的部分和
for (i = 1; i <= row; i++)
for (j = 1; j <=2* col-1; j++)
PartSum[i][j] = A[i][j] + PartSum[i - 1][j] + PartSum[i][j - 1] - PartSum[i - 1][j - 1];
int n1, n2;
int maxsofar = A[1][1];
for (n1 = 1; n1 <= row; n1++)
for (n2 = n1; n2 <= row; n2++)
{
// 将子矩阵上下边界设为第n1行和第n2行,在这些子矩阵中取最大值,类似于一维数组求最大值
int maxendinghere = MatrixSum(n1, 1, n2, 1);
for (j = 2; j <= 2*col-1; j++)
{
maxendinghere = max(MatrixSum(n1, j, n2, j), MatrixSum(n1, j, n2, j) + maxendinghere);
maxsofar = max(maxendinghere, maxsofar);
}
}
cout << maxsofar;
}
4. 运行截图
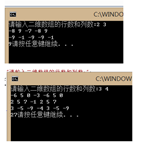
5.总结
相似的程序可以借鉴,二维数组可以转化为一维数组。对于每个程序,都要找到相似点,这样就会变得简单。



