关于线性同余方程
以前好像提及过关于同余问题,这里就不多讲了。。。
现在我要记录的,好像有些些复杂(当然,只是对于我来说)
语不惊人死不休!!
首先我要提及的是一次同余方程,形如 ax≡b(mod m)
首先我们要对同余方程ax≡b(mod m) 解的情况进行分析(要的解范围要在0到m之间,不知道为啥哈哈哈)
1.当(a,m)=1时有唯一解;(默默的提一句,最大公约数)
2.当(a,m)| b时有解,解的个数是(a,m)个
3.当(a,m) 不能整除 b时,无解;
概括一下,也就是说,我们首先要求出a与m的最大公约数,如果是b的倍数,那解的个数就是(a,m),如(a,m)不能整除b,那就是无解!!!
(至于为啥是这样的,我能力有限,就不在此讨论了,也许几年后的今天我就可以对此完善了)
那关于同余方程应该怎样求解呢?以下给出两种方法————形式分数求解(如果实在不懂,可从数学选修4-6,37页自行学习)
1.乘式求解
我们换种形式![]()
![]() ,然后分子、分母同乘以与m互素的正整数n后,在分别对分子、分母%m,使用等式右边变成整数,便得到方程唯一的解。(当然,我们要的解范围要在0到m之间)
,然后分子、分母同乘以与m互素的正整数n后,在分别对分子、分母%m,使用等式右边变成整数,便得到方程唯一的解。(当然,我们要的解范围要在0到m之间)
是不是没听懂??我来给你举个例子:7x≡8(%10) 求解x
变换形式得到x≡8/7≡8*3 / 7*3≡ 24%10/21%10 ≡4/1≡4(mod10)
其中,那个3就是“与m互素的正整数”,这可以是任何数,但是我要满足原分母(7)乘上这个数之后能模 m(就是10)之后余1(余1的目的是最后可以得到整数),所以其实核心就是经过多次变换,把分母变成1,求得解。
2.加式求解
我们依旧把他换成![]()
![]() 的形式,在分子上加上m的倍数,使新分子和分母有公约数,再约去它。最终得到的就是解。核心其实也就是让b一直加m,一直加到能让分子能整除分母即可;
的形式,在分子上加上m的倍数,使新分子和分母有公约数,再约去它。最终得到的就是解。核心其实也就是让b一直加m,一直加到能让分子能整除分母即可;
3.扩展欧几里得算法(在后面我会讲到)
那我总结一下吧(其实是贺的老师的PPT)
1. 一般的线性同余方程为ax≡b(%m),其中a≠0,b,m均为已知数,x为未知数
2.这类方程解法:先将原方程化为ax+my=b的不定方程,根据b能否整除gcd(a,m)判断方程是否有解,然后再用刚才说的那三种方法求解
3.若”d=(a,m) | b” ,b不能被d整除,则方程ax≡b(%m)无解, 否则在%m的完全剩余系{0,1,2....m-1}中,恰有d个解,第一个解为:
x0=x' * (b/d) %m,其余d-1个解可以通过对%n加上(m/d)的倍数得到,即xi=(x0+i*(m/d))%m, (1≤i≤d-1).(拓欧几里得)
代码部分:
解ax≡b(modm)方程
要求:输入三个非零整数a,b,m空格间隔。(a,b,m整型范围内),输出x的同余解,如果无解输出“no answer!”
这是解法一(扩展欧几里得)
#include<iostream> using namespace std; int a,b,m; int ex_gcd(int a,int b,int &x,int &y) { if(b==0) { x=1,y=0;return a; } int x1,y1; int d=ex_gcd(b,a%b,x1,y1); x=y1; y=x1-a/b*y1; return d; } void mod_f(int a,int b,int m) { int d,x,y,e,i; d=ex_gcd(a,m,x,y); if(b%d!=0) { printf("no answer!"); } else { e=(x*(b/d)+m)%m; for(i=0;i<d;i++) printf("%d ",(e+i*(m/d))%m); } } int main() { cin>>a>>b>>m; mod_f(a,b,m); return 0; }
关于扩展欧几里得算法我求了求旁边的大佬帮我讲了一遍,我好像是懂了吧,就是这个意思:
首先还要再提一下关于欧几里得算法和裴蜀算法哈哈
1.欧几里得算法就是辗转相除法,即gcd(a,b)=gcd(b,a%b)。
2.裴蜀算法:
a,b是整数,如果c=gcd(a,b),那么对于任意整数x,y,a*x+b*y是c的倍数。
今天我们运用的是当gcd(a,b)|c时,x,y的不定方程a*x+b*y=c(a,b,c均为整数)有整数解无数个
下面给出证明(我分为gcd(a,b)|c和不满足gcd(a,b)|c)
设r=gcd(a,b)
那么我们可以表示一下a=nr,b=mr,c=qr
y=(c-a*x)/b=(qr-nr*x)/mr=(q-n*x)/m
我们不难看出:若gcd(a,b)|c的话,q就是整数。 因为y=(q-n*x)/m,所以若y是整数,总有x是整数满足这个式子(即有x使得y为整数),所以有无数组解。
然而,如果c不能整除gcd(a,b),也就是q为小数,我们还是看y=(q-n*x)/m这个式子,(其中q是小数,m、n是整数),如果y是整数,那么由于m是整数,可以推出q-n*x一定为整数,又由于q是小数、n是整数,可以推出x一定为小数。 依照此方法,我们也可以顺利地推出若x是整数,y一定不是整数,即x,y一定不能同时取整。
ok,那么我们可以进入正题了,下面是正规题解(前两步是复制粘贴的是旁边大佬的,yyds)
首先第一步,是根据贝祖定理判断有无整数解(gcd(a,b)|c则有整数解)。那么c=n*gcd(a,b),则设x=n*q,y=n*p。所以a*q+b*p=gcd(a,b)。
接着是第二步,是运用欧几里得算法得到a*q+b*p=gcd(a,b)=gcd(b,a%b)=b*q`+(a-a/b*b)*p`=a*p`+b*(q`-a/b*p`)。
现在我们前后比对一下,a*q+b*p=a*p`+b*(q`-a/b*p`),可以看出,q对应的就是p’,而p对应的是q`-a/b*p`
(下面这句也是复制的大佬的)从而推出q,p的一组整数解,*n可得x,y的一组整数解,最终整数解有(x-k(b/gcd(a,b)),y-k(a/gcd(a,b)),因为k有无数个,所以整数解由无数个
最后一步我怎么着都看不懂了,就有问了问旁边的大佬,他是那么说的:
首先我们这样写:
a(x-k(b/gcd(a,b)))+b(y+k(a/gcd(a,b)))=c;
我们化简一下就会得到ax-abk/gcd(a,b)+by+abk/gcd(a,b)=c;
约一下就得到ax+by=c;
所以不难看出,对于任意的k(b/gcd(a,b))和k(a/gcd(a,b))(其中k是常数,可以是任何数)
对于x,每过一个a/gcd(a,b)就会产生一组新的解,对于y,每过一个b/gcd(a,b)就会一组新的解。
所以就会有x-k(b/gcd(a,b)),y-k(a/gcd(a,b)组解。因为k可以是任何数,所以有无数组解。
下面我再给你举个例子:
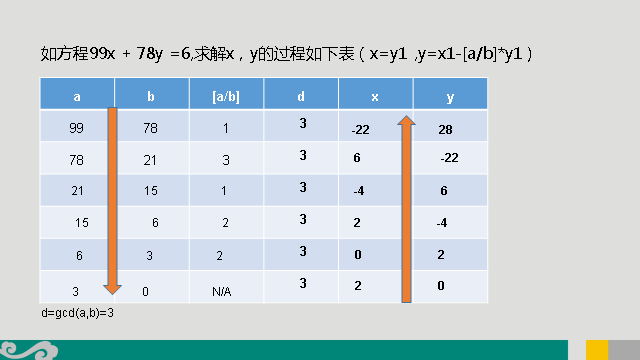
首先,我们可以通过gcd(a,b)=gcd(b,a%b)这个递归解得gcd(a,b)是多少,并要记录每一次的a/b,然后我们再看最后两列,我们要从下往上推,先用6/3得到2,让x=2,y=0,这样我们就得到了最低行的等式,即ax+by=6(即3*2+0=6);就这样,我们再让x等于y1,让y等于x1-[a-b]*y1(我们把x和y定义为新的解,而x1和y1为原来的解),这样我们又得到了第二组的等式ax+by=6 (即6*0+2*3=6)那我们就能明白他的用意了,其实每一行的a,b,x,y都能满足那个ax+by=6的等式,一开始a是3,b是0,然后一直推推推,让x=y1,y=x1-[a-b]*y1,得到新的等式,最后a会变成99,b会变成78,此时推过来的x和y,就是可以满足这个等式的解
其实代码也就是这样体现的。
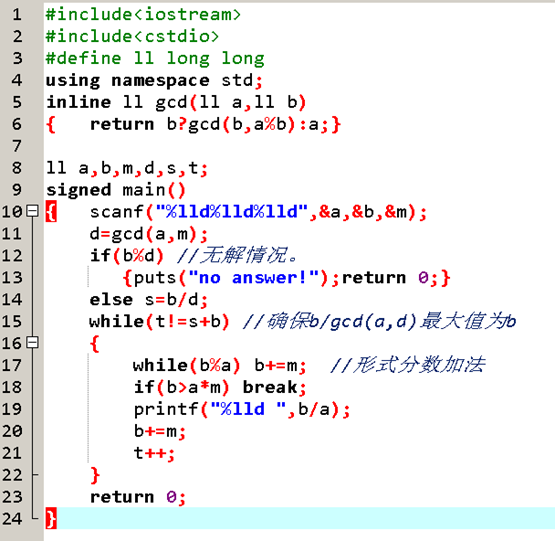
这是解法二 ———形式分数加法代码
其实思路就是我刚才讲的,直接上代码吧(还是复制PPT)
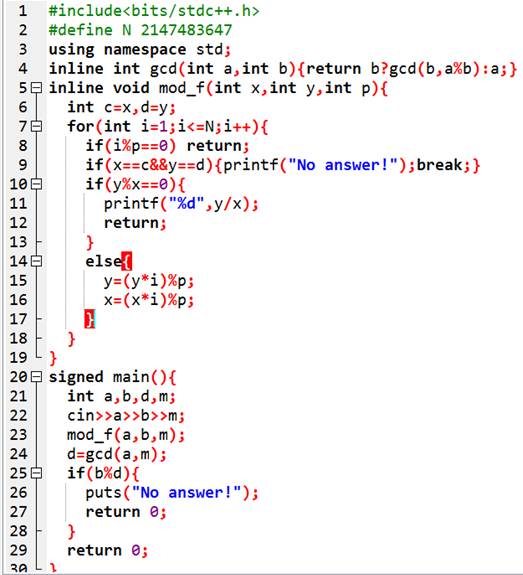
解法三————形式分数乘法
思路也是刚才提到的,也直接上代码吧(复制PPT)
那你可能就顿悟怎么解多元一次不定方程了吧,不接受任何反驳
上例题!
输入a,b,c,d,n 请找出一组整数解(x1,x2,x3,x4)满足:a*x1+b*x2+c*x3+d*x4=n
思路就是这样的: 我们先与处理掉gcd(a,b,c),然后原式就变成了 gcd(a,b,c)*y1+d*x4=n;我们运用所学知识就可以解出一组解,解出x4,d和y1;
然后列出第二组方程,a*x1+b*x2+c*x3=gcd(a,b,c)*y1 由于我们能求出gcd(a,b,c)而且已经求出了y1,我们就可以得到新的一组方程,然后一直重复以上操作,就可以得出一组解集
代码如下


好了,终于讲完了!!
太伤元气了,我要去开摆了,再见!!




