1.简单括号匹配
| ''' |
| 下面看看如何构造括号匹配识别算法 |
| |
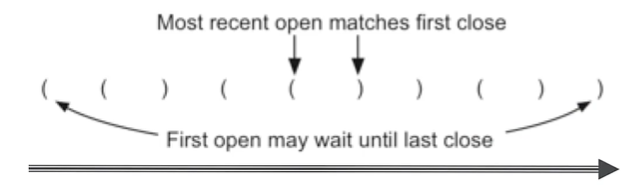
| 从左到右扫描括号串,最新打开的左括号,应该匹配最先遇到的右括号,这样第一个左括号(最左打开),就应该匹配最后一个右括号(最后遇到) |
| 这种次序反转的识别,正好符合栈的特性! |
| ''' |
| |
| from pythonds.basic.stack import Stack |
| |
| def parChecker(symbolString): |
| s = Stack() |
| balanced = True |
| index = 0 |
| while index < len(symbolString) and balanced: |
| symbol = symbolString[index] |
| if symbol == "(": |
| s.push(symbol) |
| else: |
| if s.isEmpty(): |
| balanced = False |
| else: |
| s.pop() |
| index = index +1 |
| |
| if balanced and s.isEmpty(): |
| return True |
| else: |
| return False |
| |
| print(parChecker('((()))')) |
| print(parChecker('(()()(()))')) |
| |
| print(parChecker('(()')) |
| |
| |
| ''' |
| 在实际的应用里,我们会碰到更多中括号 |
| 如python中列表所用的方括号"[]" |
| 字典所有的花括号"{}" |
| 元组和表达式所用的圆括号"()" |
| 这些不同的括号有可能混合在一起使用,因此就要注意各自的开闭匹配情况。 |
| |
| 下面这些是匹配的 |
| { { ( [ ] [ ] ) } ( ) } |
| [ [ { { ( ( ) ) } } ] ] |
| [ ] [ ] [ ] ( ) { } |
| |
| 下面这些是不匹配的 |
| ( [ ) ] |
| [ { ( )] } |
| ( ( ( ) ] ) ) |
| ''' |
| ''' |
| 通用括号匹配算法:代码 |
| 需要修改的地方:碰到各种左括号仍然入栈,碰到各种右括号的时候需要判断栈顶的左括号是否当前括号同一种类 |
| ''' |
| from pythonds.basic.stack import Stack |
| |
| def parChecker(symbolString): |
| s = Stack() |
| balanced = True |
| index = 0 |
| while index < len(symbolString) and balanced: |
| symbol = symbolString[index] |
| if symbol in "({[": |
| s.push(symbol) |
| else: |
| if s.isEmpty(): |
| balanced = False |
| else: |
| top = matchs(symbol,s) |
| if top: |
| s.pop() |
| else: |
| balanced = False |
| |
| index = index +1 |
| |
| if balanced and s.isEmpty(): |
| return True |
| else: |
| return False |
| |
| def matchs(symbol,s): |
| s_symbol =s.peek() |
| if symbol == ")": |
| if s_symbol == "(": |
| return True |
| else: |
| return False |
| if symbol == "}": |
| if s_symbol == "{": |
| return True |
| else: |
| return False |
| if symbol == "]": |
| if s_symbol == "[": |
| return True |
| else: |
| return False |
| |
| print(parChecker('((()))')) |
| print(parChecker('(()()(()))')) |
| print(parChecker("[{()]}")) |
| 此外,HTML/XML文档也有类似于括号的开闭标记,这种层次结构化文档的校验、操作也可以通过栈来实现 |

不使用栈进行符号的匹配检测的实现方式:
| |
| def check(expression): |
| open_tup = tuple('({[') |
| close_tup = tuple(')}]') |
| map = dict(zip(open_tup,close_tup)) |
| queue = [] |
| |
| for i in expression: |
| if i in open_tup: |
| queue.append(map[i]) |
| elif i in close_tup: |
| if not queue or i != queue.pop(): |
| return "Unbalanced" |
| |
| if not queue: |
| return "Balanced" |
| |
| else: |
| return "Unbalanced" |
| |
| |
| string = "{[]{()}}" |
| print(string, "-",check(string)) |
| |
| string = "((()" |
| print(string, "-", check(string)) |
2.十进制转换为二进制
| ''' |
| “除以2”的过程,得到的余数是从低到高的次序,而输出则是从高到低,所以需要一个栈来反转次序 |
| ''' |

| from pythonds.basic.stack import Stack |
| |
| def divideBy2(decNumber): |
| remstack = Stack() |
| while decNumber > 0: |
| rem = decNumber % 2 |
| remstack.push(rem) |
| decNumber = decNumber // 2 |
| |
| binString = '' |
| while not remstack.isEmpty(): |
| binString = binString + str(remstack.pop()) |
| return binString |
| |
| print(divideBy2(42)) |
3.十进制转换为十六以下任意进制代码
| from pythonds.basic.stack import Stack |
| |
| def baseConberter(decNumber,base): |
| digits = "0123456789ABCDEF" |
| |
| remstack = Stack() |
| |
| while decNumber > 0: |
| rem = decNumber % base |
| remstack.push(rem) |
| decNumber = decNumber // base |
| |
| newString = "" |
| while not remstack.isEmpty(): |
| newString = newString+digits[remstack.pop()] |
| |
| return newString |
| |
| print(baseConberter(25,2)) |
| print(baseConberter(25,16)) |
4.通用的中缀转后缀算法
| 在中缀表达式转换为后缀形式的处理过程中,操作符比操作数要晚输出,所以在扫描到对应的第二个操作数之前,需要把操作符先保存起来,而这些暂存的操作符,由于优先级的规则,还有可能要反转的次序输出。 |
| 在A+B*C中,+虽然先出现,但优先级比后面这个*要低,所以它要等*处理完后,才能再处理。 |
| 这种反转特性,使得我们考虑用栈来保存暂时未处理的操作符。 |
| |
| 再看看(A+B)*C,对应的后缀形式是AB+C*,这里+的输出比*要早,主要是因为括号使得+得优先级提升,高于括号之外得*。回顾上节得“全括号”表达式,后缀表达式中操作符应该出现在左括号对应的右括号位置,所以遇到左括号,要标记下,其后出现的操作符优先级提升了,一旦扫描到对应的右括号,就可以马上输出这个操作符。 |
| |
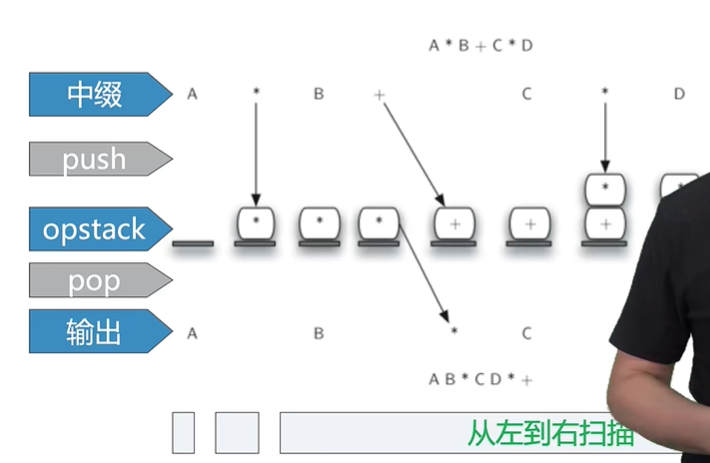
| 总结:在从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符,这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再行处理。 |
| 后面的算法描述中,约定中缀表达式是由空格隔开的一系列单词(token)构成,操作符单词包括*/+-(),而操作数单词则是单词字母标识符A、B、C等。 |
| 首先,创建空栈opstack用于暂存操作符,空表postfixList用于保存后缀表达式,将中缀表达式转换为单词(token)列表 |
| A+B*C = split=> ["A","+","B","*","C"] |
| |
| |
| 如果单词是操作数,则直接添加到后缀表达式列表的末尾; |
| 如果单词是左括号"(",则压入opstack栈顶; |
| 如果单词是右括号")",则反复弹出opstack栈顶操作符,加入到输出列表末尾,直到碰到左括号; |
| 如果单词是操作符"*/+-",则压入opstack栈顶 |
| |
| 但在压入之前,要比较其与栈顶操作符的优先级。如果栈顶的高于或等于它,就要反复弹出栈顶操作符,加入到输出列表末尾,直到栈顶的操作符优先级低于它。 |
| |
| 中缀表达式单词列表扫描结束后,把opstack栈中的所有剩余操作符一次弹出,添加到输出列表末尾。把输出列表再用join方法合并成后缀表达式字符串,算法结束。 |
| 以 (A+B)*(C+D) |
| |
| from pythonds.basic.stack import Stack |
| |
| from pythonds.basic.stack import Stack |
| |
| def infixToPostfix(infixexpr): |
| prec = {} |
| prec['*'] = 3 |
| prec['/'] = 3 |
| prec['+'] = 2 |
| prec['-'] = 2 |
| prec['('] = 1 |
| opStack = Stack() |
| postfix_list = [] |
| tokenList = list(infixexpr) |
| |
| print(tokenList) |
| |
| for token in tokenList: |
| if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ": |
| postfix_list.append(token) |
| elif token == "(": |
| opStack.push(token) |
| elif token == ")": |
| topToken = opStack.pop() |
| while topToken != '(': |
| postfix_list.append(topToken) |
| topToken = opStack.pop() |
| else: |
| while (not opStack.isEmpty()) and (prec[opStack.peek()] >= prec[token]): |
| postfix_list.append(opStack.pop()) |
| opStack.push(token) |
| |
| while not opStack.isEmpty(): |
| postfix_list.append(opStack.pop()) |
| print(postfix_list) |
| return ''.join(postfix_list) |
| |
| print(infixToPostfix('(A+B)*(C+D)')) |
5.后缀表达式求值
| 跟中缀转换为后缀问题不同,在对后缀表达式从左到右扫描的过程中,由于操作符在操作数的后面,所以要暂存操作数,在碰到操作符的时候,再将暂存的两个操作数进行实际的计算。 |
| 仍然是栈的特性:操作符只作用于离它最近的两个操作数。 |
| |
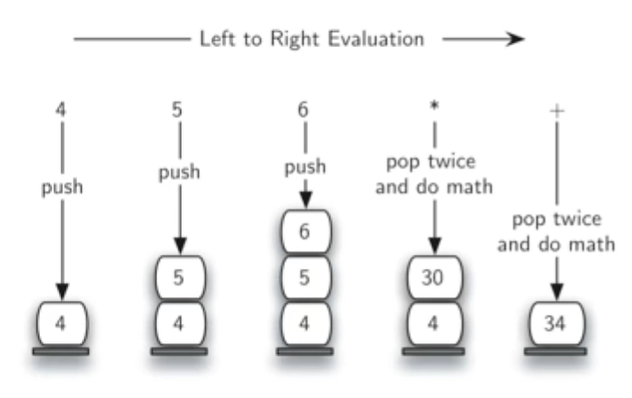
| 如“4 5 6 * +”,我们先扫描到4、5两个操作数,但还不知道对这两个操作数能做什么计算,需要继续扫描后面符号才能知道。继续扫描,又碰到操作数6,还是不能知道如何计算,继续暂存入栈,直到“*”,现在直到是栈顶两个操作数5、6做乘法。我们弹出两个操作数,计算得到结果30,需要注意:先弹出的是右操作数,后弹出的是左操作数,这个对于-/很重要! |
| 为了继续后续的计算,需要把这个中间结果30压入栈顶,继续扫面后面的符号,当所有操作符都处理完毕,栈中只留下1个操作数,就是表达式的值。 |
例1:
例2:
![image-20221118161740691]()
| 创建空栈operandStack用于暂存操作数 |
| 将后缀表达式用split方法解析为单词(token)的列表 |
| 从左到右扫描单词列表,如果单词是一个操作数,将单词转换为整数int,压入operandStack栈顶;如果单词是一个操作符(*/+-),就开始求职,从栈顶弹出2个操作数,先弹出的是右操作数,后弹出的是左操作数,计算后将值重新压入栈顶。单词列表扫描结束后,表达式的值就在栈顶,弹出栈顶的值,返回。 |
| from pythonds.basic.stack import Stack |
| def postfixEval(postfixExpr): |
| |
| operandStack = Stack() |
| tokenList = list(postfixExpr) |
| |
| for token in tokenList: |
| if token in "0123456789": |
| operandStack.push(int(token)) |
| else: |
| operand2 = operandStack.pop() |
| operand1 = operandStack.pop() |
| result = doMath(token, operand1, operand2) |
| operandStack.push(result) |
| |
| return operandStack.pop() |
| |
| |
| def doMath(op,op1,op2): |
| if op == "*": |
| return op1 * op2 |
| elif op == "/": |
| return op1 / op2 |
| elif op == "+": |
| return op1 + op2 |
| else: |
| return op1 - op2 |
| |
| |
| print(postfixEval('456+*')) |
| print(postfixEval('45+6*')) |







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!