bzoj4008 [HNOI2015]亚瑟王
4008: [HNOI2015]亚瑟王
Time Limit: 20 Sec Memory Limit: 512 MBSec Special JudgeSubmit: 1859 Solved: 1091
[Submit][Status][Discuss]
Description
小 K 不慎被 LL 邪教洗脑了,洗脑程度深到他甚至想要从亚瑟王邪教中脱坑。
他决定,在脱坑之前,最后再来打一盘亚瑟王。既然是最后一战,就一定要打得漂
亮。众所周知,亚瑟王是一个看脸的游戏,技能的发动都是看概率的。作为一个非
洲人,同时作为一个前 OIer,小 K 自然是希望最大化造成伤害的期望值。但他已
经多年没写过代码,连 Spaly都敲不对了,因此,希望你能帮帮小 K,让他感受一
下当欧洲人是怎样的体验。
本题中我们将考虑游戏的一个简化版模型。
玩家有一套卡牌,共 n张。游戏时,玩家将 n 张卡牌排列成某种顺序,排列后
将卡牌按从前往后依次编号为 1 ~ n。本题中,顺序已经确定,即为输入的顺序。
每张卡牌都有一个技能。第 i 张卡牌的技能发动概率为 pi,如果成功发动,则会对
敌方造成di点伤害。也只有通过发动技能,卡牌才能对敌方造成伤害。基于现实因
素以及小K非洲血统的考虑,pi不会为 0,也不会为 1,即 0 < pi < 1。
一局游戏一共有 r 轮。在每一轮中,系统将从第一张卡牌开始,按照顺序依次
考虑每张卡牌。在一轮中,对于依次考虑的每一张卡牌:
1如果这张卡牌在这一局游戏中已经发动过技能,则
1.1 如果这张卡牌不是最后一张,则跳过之(考虑下一张卡牌);
否则(是最后一张),结束这一轮游戏。
2否则(这张卡牌在这一局游戏中没有发动过技能),设这张卡牌为第 i 张
2.1将其以 pi的概率发动技能。
2.2如果技能发动,则对敌方造成 di点伤害,并结束这一轮。
2.3如果这张卡牌已经是最后一张(即 i 等于n),则结束这一轮;否则,
考虑下一张卡牌。
请帮助小 K 求出这一套卡牌在一局游戏中能造成的伤害的期望值。
Input
输入文件的第一行包含一个整数 T,代表测试数据组数。
接下来一共 T 组数据。
每组数据的第一行包含两个用空格分开的整数 n和r,分别代表卡牌的张数和
游戏的轮数。
接下来 n行,每行包含一个实数和一个整数,由空格隔开,描述一张卡牌。第
i 行的两个数为 pi和 di,分别代表第 i 张卡牌技能发动的概率(实数)和技能发动
造成的伤害(整数)。保证 pi最多包含 4位小数,且为一个合法的概率。
Output
对于每组数据,输出一行,包含一个实数,为这套卡牌在这一局游戏中造成的
伤害的期望值。对于每一行输出,只有当你的输出和标准答案的相对误差不超过
10^-8时——即|a-o|/a<=10-8时(其中a是标准答案,o是输出),你的输出才会被判为正确。
建议输出10 位小数。
Sample Input
1
3 2
0.5000 2
0.3000 3
0.9000 1
3 2
0.5000 2
0.3000 3
0.9000 1
Sample Output
3.2660250000
HINT
一共有 13 种可能的情况:
1. 第一轮中,第 1张卡牌发动技能;第二轮中,第 2张卡牌发动技能;
概率为 0.15,伤害为5。
2. 第一轮中,第 1张卡牌发动技能;第二轮中,第 3张卡牌发动技能;
概率为 0.315,伤害为3。
3. 第一轮中,第 1张卡牌发动技能;第二轮不发动技能;
概率为 0.035,伤害为2。
4. 第一轮中,第 2张卡牌发动技能;第二轮中,第 1张卡牌发动技能;
概率为 0.075,伤害为5。
5. 第一轮中,第 2张卡牌发动技能;第二轮中,第 3张卡牌发动技能;
概率为 0.0675,伤害为4。
6. 第一轮中,第 2张卡牌发动技能;第二轮不发动技能;
概率为 0.0075,伤害为3。
7. 第一轮中,第 3张卡牌发动技能;第二轮中,第 1张卡牌发动技能;
概率为 0.1575,伤害为3。
8. 第一轮中,第 3张卡牌发动技能;第二轮中,第 2张卡牌发动技能;
概率为 0.04725,伤害为4。
9. 第一轮中,第 3张卡牌发动技能;第二轮不发动技能;
概率为 0.11025,伤害为1。
10. 第一轮不发动技能;第二轮中,第 1张卡牌发动技能;
概率为 0.0175,伤害为2。
11. 第一轮不发动技能;第二轮中,第 2张卡牌发动技能;
概率为 0.00525,伤害为3。
12. 第一轮不发动技能;第二轮中,第 3张卡牌发动技能;
概率为 0.011025,伤害为1。
13. 第一轮不发动技能;第二轮亦不发动技能;
概率为 0.001225,伤害为0。
造成伤害的期望值为概率与对应伤害乘积之和,为 3.266025。
对于所有测试数据, 1 <= T <= 444, 1 <= n <= 220, 0 <= r <= 132, 0 < pi < 1, 0 <= di <= 1000。
除非备注中有特殊说明,数据中 pi与di均为随机生成。
请注意可能存在的实数精度问题,并采取适当措施。
分析:一道比较神的期望dp题.
一开始想着令![]() 表示前i个人前j轮造成伤害的期望值. 从
表示前i个人前j轮造成伤害的期望值. 从![]() 转移到
转移到![]() ,发现第
,发现第![]() 个人的概率不好算.
个人的概率不好算.
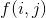 表示前i个人前j轮造成伤害的期望值. 从
表示前i个人前j轮造成伤害的期望值. 从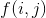 转移到
转移到 ,发现第
,发现第 个人的概率不好算.
个人的概率不好算. 换一个状态表示.令![]() 表示前i个人还剩j轮造成伤害的期望值. 那么第i+1个人不被选中的概率就是
表示前i个人还剩j轮造成伤害的期望值. 那么第i+1个人不被选中的概率就是![]() .被选中的概率可以利用补集思想求得:
.被选中的概率可以利用补集思想求得:![]() . 状态转移方程就出来了.
. 状态转移方程就出来了.
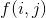 表示前i个人还剩j轮造成伤害的期望值. 那么第i+1个人不被选中的概率就是
表示前i个人还剩j轮造成伤害的期望值. 那么第i+1个人不被选中的概率就是 .被选中的概率可以利用补集思想求得:
.被选中的概率可以利用补集思想求得: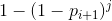 . 状态转移方程就出来了.
. 状态转移方程就出来了. 求出来发现答案是错的.为什么呢?因为概率顺推,期望倒推!那么枚举顺序和状态表示的意义就都要改变. ![]() 表示前i个人前j轮造成伤害的期望值. 表示的是结果状态,那么第i个人不被选中的概率就是
表示前i个人前j轮造成伤害的期望值. 表示的是结果状态,那么第i个人不被选中的概率就是![]() (选了j轮都没有被选中),不被选中的概率同理. 倒推即可.最后的答案是f(1,r).
(选了j轮都没有被选中),不被选中的概率同理. 倒推即可.最后的答案是f(1,r).
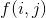 表示前i个人前j轮造成伤害的期望值. 表示的是结果状态,那么第i个人不被选中的概率就是
表示前i个人前j轮造成伤害的期望值. 表示的是结果状态,那么第i个人不被选中的概率就是 (选了j轮都没有被选中),不被选中的概率同理. 倒推即可.最后的答案是f(1,r).
(选了j轮都没有被选中),不被选中的概率同理. 倒推即可.最后的答案是f(1,r).
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; int T,n,r; double f[230][140],p[230],d[230]; double qpow(double a,int b) { double res = 1.0; while (b) { if (b & 1) res *= a; b >>= 1; a *= a; } return res; } int main() { scanf("%d",&T); while (T--) { memset(f,0,sizeof(f)); scanf("%d%d",&n,&r); for (int i = 1; i <= n; i++) scanf("%lf%lf",&p[i],&d[i]); for (int i = n; i >= 1; i--) for (int j = 1; j <= r; j++) { double temp = qpow(1.0 - p[i],j); double temp2 = 1.0 - temp; f[i][j] += f[i + 1][j] * temp; f[i][j] += temp2 * (f[i + 1][j - 1] + d[i]); } printf("%.10lf\n",f[1][r]); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号