bzoj4872 [Shoi2017]分手是祝愿

4872: [Shoi2017]分手是祝愿

Time Limit: 20 Sec  Memory Limit: 512 MB
Submit: 513  Solved: 339
[Submit][Status][Discuss]

Description

Zeit und Raum trennen dich und mich.

时空将你我分开。B 君在玩一个游戏，这个游戏由 n 个灯和 n 个开关组成，给定这 n 个灯的初始状态，下标为

从 1 到 n 的正整数。每个灯有两个状态亮和灭，我们用 1 来表示这个灯是亮的，用 0 表示这个灯是灭的，游戏

的目标是使所有灯都灭掉。但是当操作第 i 个开关时，所有编号为 i 的约数（包括 1 和 i）的灯的状态都会被

改变，即从亮变成灭，或者是从灭变成亮。B 君发现这个游戏很难，于是想到了这样的一个策略，每次等概率随机

操作一个开关，直到所有灯都灭掉。这个策略需要的操作次数很多， B 君想到这样的一个优化。如果当前局面，

可以通过操作小于等于 k 个开关使所有灯都灭掉，那么他将不再随机，直接选择操作次数最小的操作方法（这个

策略显然小于等于 k 步）操作这些开关。B 君想知道按照这个策略（也就是先随机操作，最后小于等于 k 步，使

用操作次数最小的操作方法）的操作次数的期望。这个期望可能很大，但是 B 君发现这个期望乘以 n 的阶乘一定

是整数，所以他只需要知道这个整数对 100003 取模之后的结果。

Input

第一行两个整数 n, k。

接下来一行 n 个整数，每个整数是 0 或者 1，其中第 i 个整数表示第 i 个灯的初始情况。

1 ≤ n ≤ 100000, 0 ≤ k ≤ n；

Output

输出一行，为操作次数的期望乘以 n 的阶乘对 100003 取模之后的结果。

Sample Input

4 0
0 0 1 1

Sample Output

512

分析：挺难的一道题.

　　　首先考虑当n = k时要如何做.  从大到小枚举，如果这个灯没有被关上，就必须把它关上，因为后面没有灯能关上它了. 关上这个灯后把它的约数编号的灯的状态取反. 这就是最优策略.

　　　容易发现，最优策略中操作的灯是一定要被操作的.（因为编号比它大的没有被关上的灯都不是它的倍数）. 求期望，考虑dp:

令f[i]表示还剩下i盏必须要被操作的灯 的期望操作步数.  下一次操作有i/n的概率操作到必须被操作的灯.  有(n - i)/n的概率操作到不能被操作的灯. 这样期望操作步数就会+1（将不能被操作的灯给变回来）.

　　　f[i] = (i / n) * f[i - 1] + ((n - i) / n) * f[i + 1] + 1.  

　　　这个状态转移方程显然是不能直接递推的. 有点像解方程组,用高斯消元法吗？ 复杂度太高. 正确的做法是换元！

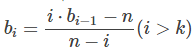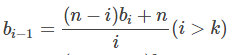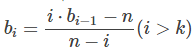　　　令bi = f[i+1] + f[i]. 可以得到：. 强调i > k是因为当i ≤ k时，f[i] = i.（按照最优策略这些灯都要被操作一次）. 由于不知道b[k]的值，这个式子是不能递推下去的.  但是没关系，把正推的式子改成逆推即可：.

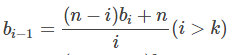f[n] = n,b[n - 1] = f[n - 1] - f[n] = 1. 这样就能够递推了.

　　　这道题挺神奇的，直接dp很难想，先要通过分析最优策略得出结论：有一些灯必须被操作. 根据这个结论就能得到状态表示以及状态转移方程. 通过换元来实现递推. 因为边界问题，对递推式进行等价变形来实现逆推.

 

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;
const ll maxn = 100010,mod = 100003;
ll n,k,a[maxn],cnt,b[maxn],ni[maxn],f[maxn];
vector <ll> p[maxn];

int main()
{
    scanf("%lld%lld",&n,&k);
    ni[1] = 1;
    for (ll i = 2; i <= n; i++)
        ni[i] = (mod - mod / i) * ni[mod % i] % mod;
    for (ll i = 1; i <= n; i++)
        for (ll j = i; j <= n; j += i)
            p[j].push_back(i);
    for (ll i = 1; i <= n; i++)
        scanf("%lld",&a[i]);
    for (ll i = n; i >= 1; i--)
    {
        if (a[i] == 1)
        {
            cnt++;
            a[i] = 0;
            for (ll j = 0; j < p[i].size(); j++)
                a[p[i][j]] ^= 1;
        }
    }
    b[n - 1] = 1;
    for (ll i = n - 2; i >= k; i--)
    {
        ll temp = (n - i - 1) * b[i + 1] % mod;
        temp += n;
        temp %= mod;
        temp *= ni[i + 1];
        temp %= mod;
        b[i] = temp;
    }
    for (ll i = 0; i < k; i++)
        b[i] = 1;
    f[0] = 0;
    for (ll i = 0; i < n; i++)
        f[i + 1] = f[i] + b[i];
    for (ll i = 1; i <= n; i++)
        f[cnt] = (f[cnt] * i) % mod;
    printf("%lld\n",f[cnt]);

    return 0;
}