bzoj3527 [Zjoi2014]力

3527: [Zjoi2014]力

Time Limit: 30 Sec  Memory Limit: 256 MBSec  Special Judge
Submit: 2803  Solved: 1698
[Submit][Status][Discuss]

Description

给出n个数qi，给出Fj的定义如下：

令Ei=Fi/qi，求Ei.

Input

第一行一个整数n。

接下来n行每行输入一个数，第i行表示qi。

n≤100000，0<qi<1000000000

Output

 n行，第i行输出Ei。与标准答案误差不超过1e-2即可。

Sample Input

5
4006373.885184
15375036.435759
1717456.469144
8514941.004912
1410681.345880

Sample Output

-16838672.693
3439.793
7509018.566
4595686.886
10903040.872

分析：别人眼中是一道很裸的FFT的题，我却想了很长时间.

　　　首先把qi给约掉. 左右两个式子明显不同，分开计算. 因为要求所有的Ei的值，一个一个单独计算肯定会超时，题目所给的范围是O(nlogn)的算法能够承受的,想到用FFT. 

　　　用FFT就要把这个式子转化成卷积的形式. 看上去似乎无从下手......举个简单的例子找找规律就好啦.

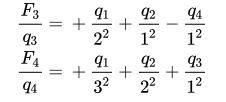　　　，先分析加法的那一部分. 可以找到规律：qi / j^2,  如果i + j == k,那么Ek一定会统计这个答案. 这就是卷积的形式了.  令ai = qi, bi = 1/i^2.  多项式乘法，套用FFT模板，得到的第k项就是Ek的加法部分的值.

　　　重点讲减法部分,这是当初令我十分疑惑的地方.先找规律，如果i - j == k,那么Ek一定会统计这个答案. 这好像不能直接用卷积来做. 怎么办呢？

　　　把下标强行变成i' + j' == k'的形式,然后利用下标替换变成我们找到的规律的式子：i - j == k,具体是这样的：

　　　首先把i变成n - i - 1，也就是把ai数组倒过来.  为了消掉这个n, 把k变成n - k - 1. 化简就变成了i - j == k. 那么方法就出来了：

　　　1.先把a数组倒过来.

　　　2.求得卷积后把答案数组倒过来，第k项即Ek的答案.

　　　最后两次卷积相减就能得到答案了.

　　　用FFT解题首先要能看出这道题能用FFT解. 即要求多个项的答案，两个多项式相乘并且下标和与项的下标之间有规律. 将i + j == k通过坐标代换变成下标之间的关系式.  根据这个代换的过程，就能知道要怎么处理了.

#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 500010;
const double pai = acos(-1.0);
double a[maxn],b[maxn],ans[maxn];
int n,len;

struct node
{
    double real, imag;
    node(double real = 0.0, double imag = 0.0)
    {
        this->real = real, this->imag = imag;
    }
    node operator - (const node&elem) const
    {
        return node(this->real - elem.real, this->imag - elem.imag);
    }
    node operator + (const node&elem) const
    {
        return node(this->real + elem.real, this->imag + elem.imag);
    }
    node operator * (const node&elem) const
    {
        return node(this->real * elem.real - this->imag * elem.imag, this->real * elem.imag + this->imag * elem.real);
    }
    void set(double real = 0.0, double imag = 0.0)
    {
        this->real = real, this->imag = imag;
    }
} A[maxn],B[maxn];

void pre1()
{
    len = 1;
    while(len < (n << 1))
        len <<= 1;
    for (int i = 0; i < n; i++)
        A[i].set(a[i],0),B[i].set(b[i],0);
    for (int i = n; i < len; i++)
        A[i].set(),B[i].set();
}

void pre2()
{
    len = 1;
    while(len < (n << 1))
        len <<= 1;
    for (int i = 0; i < len; i++)
        A[i].set(),B[i].set();
    for (int i = 0; i < n; i++)
    {
        A[i].set(a[n - i - 1],0);
        if (i)
            B[i].set(b[i],0);
    }
    for (int i = n; i < len; i++)
        A[i].set(),B[i].set();
}

void Swap(node &a,node &b)
{
    node temp = a;
    a = b;
    b = temp;
}

void zhuan(node *y)
{
    for (int i = 1, j = len >> 1,k; i < len - 1; i++)
    {
        if (i < j)
            Swap(y[i],y[j]);
        k = len >> 1;
        while (j >= k)
        {
            j -= k;
            k >>= 1;
        }
        if (j < k)
            j += k;
    }
}

void FFT(node *y,int op)
{
    zhuan(y);
    for (int h = 2; h <= len; h <<= 1)
    {
        node temp(cos(2 * pai * op / h),sin(2 * pai * op / h));
        for (int i = 0; i < len; i += h)
        {
            node W(1,0);
            for (int j = i; j < i + h / 2; j++)
            {
                node u = y[j],v = W * y[j + h / 2];
                y[j] = u + v;
                y[j + h / 2] = u - v;
                W = W * temp;
            }
        }
    }
    if (op == -1)
        for (int i = 0; i < len; i++)
            y[i].real /= len;
}

void solve(node *A,node *B)
{
    FFT(A,1);
    FFT(B,1);
    for (int i = 0; i < len; i++)
        A[i] = A[i] * B[i];
    FFT(A,-1);
}

int main()
{
    scanf("%d",&n);
    for (int i = 0; i < n; i++)
        scanf("%lf",&a[i]);
    for (int i = 1; i < n; i++)
        b[i] = 1.0 / i / i;
    pre1();
    solve(A,B);
    for (int i = 0; i < n; i++)
        ans[i] = A[i].real;
    pre2();
    solve(A,B);
    for (int i = 0; i < n; i++)
        ans[i] -= A[n - i - 1].real;
    for (int i = 0; i < n; i++)
        printf("%.3lf\n",ans[i]);

    return 0;
}