bzoj4827 [Hnoi2017]礼物

4827: [Hnoi2017]礼物

Time Limit: 60 Sec  Memory Limit: 512 MB
Submit: 727  Solved: 504
[Submit][Status][Discuss]

Description

我的室友最近喜欢上了一个可爱的小女生。马上就要到她的生日了，他决定买一对情侣手 环，一个留给自己，一

个送给她。每个手环上各有 n 个装饰物，并且每个装饰物都有一定的亮度。但是在她生日的前一天，我的室友突

然发现他好像拿错了一个手环，而且已经没时间去更换它了！他只能使用一种特殊的方法，将其中一个手环中所有

装饰物的亮度增加一个相同的自然数 c（即非负整数）。并且由于这个手环是一个圆，可以以任意的角度旋转它，

但是由于上面 装饰物的方向是固定的，所以手环不能翻转。需要在经过亮度改造和旋转之后，使得两个手环的差

异值最小。在将两个手环旋转且装饰物对齐了之后，从对齐的某个位置开始逆时针方向对装饰物编号 1,2,…,n，

其中 n 为每个手环的装饰物个数，第 1 个手环的 i 号位置装饰物亮度为 xi，第 2 个手 环的 i 号位置装饰物

亮度为 yi，两个手环之间的差异值为(参见输入输出样例和样例解释)：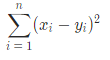

 

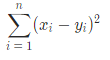
麻烦你帮他

计算一下，进行调整（亮度改造和旋转），使得两个手环之间的差异值最小， 这个最小值是多少呢？

Input

输入数据的第一行有两个数n, m，代表每条手环的装饰物的数量为n，每个装饰物的初始 亮度小于等于m。

接下来两行，每行各有n个数，分别代表第一条手环和第二条手环上从某个位置开始逆时 针方向上各装饰物的亮度。

1≤n≤50000, 1≤m≤100, 1≤ai≤m

Output

输出一个数，表示两个手环能产生的最小差异值。

注意在将手环改造之后，装饰物的亮度 可以大于 m。

Sample Input

5 6
1 2 3 4 5
6 3 3 4 5

Sample Output

1
【样例解释】
需要将第一个手环的亮度增加1，第一个手环的亮度变为： 2 3 4 5 6 旋转一下第二个手环。对于该样例，是将第
二个手环的亮度6 3 3 4 5向左循环移动 一个位置，使得第二手环的最终的亮度为
：3 3 4 5 6。 此时两个手环的亮度差异值为1。

分析：好题！

　　　很容易想到：只需要考虑一个手环亮度的变化. 这样另一个的亮度变化就是相对于当前手环的了,和考虑2个手环亮度的变化是等价的.

　　　题目中给了答案的计算公式，将亮度的变化c带入进式子中，得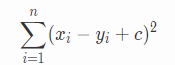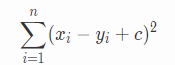：,展开，可以得到：

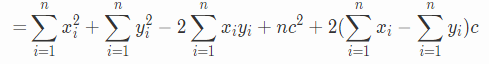. 这种展开方式是处理复杂的带Σ式子的常用方法，即：将结构相同的单独提出来，再对每一项分别求解.

　　　前两项维护两个前缀和就好了.  后面的有关c的式子实际上是一个二次函数ax^2 + bx. a和b都确定了，x的最值也就确定了. 关键是如何使得2Σxiyi最大.

　　　这显然是不能O(n)出解的. 必须将每一种相对的方式都考虑到才能得到正确的答案. 也就是说，我们需要固定x,每次将y整体向后挪一位，挪n次，算出每次的最大值. 

　　　直接算是O(n^2)的，有没有什么快一点的方法呢？ 其实它可以用FFT优化到O(nlogn).

　　　看到两项相乘，又带个∑符号，复杂度要求O(nlogn)的，基本上就是FFT了.  如果y向后挪了k位，那么f[k] = Σx[i] * y[i + k]. 这就和bzoj2194是一模一样的了.

　　　需要注意的是：本题中的数是循环的，也就是说a_i + k 可能在a_i之前（转回来了），那么就需要把a数组在其后面复制一份.（破环成链）.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;
typedef long long ll;
const ll maxn = 500010,inf = 1LL << 60;
const double pai = acos(-1.0);
ll n,m,a[maxn],b[maxn],ans,sum1,sum2,sum11,sum22,pos1,pos2,len;

struct node
{
    double real, imag;
    node(double real = 0.0, double imag = 0.0)
    {
        this->real = real, this->imag = imag;
    }
    node operator - (const node&elem) const
    {
        return node(this->real - elem.real, this->imag - elem.imag);
    }
    node operator + (const node&elem) const
    {
        return node(this->real + elem.real, this->imag + elem.imag);
    }
    node operator * (const node&elem) const
    {
        return node(this->real * elem.real - this->imag * elem.imag, this->real * elem.imag + this->imag * elem.real);
    }
    void set(double real = 0.0, double imag = 0.0)
    {
        this->real = real, this->imag = imag;
    }
} A[maxn],B[maxn];

void Swap(node &a,node &b)
{
    node temp = a;
    a = b;
    b = temp;
}

void zhuan(node *y)
{
    for (ll i = 1,j = len >> 1,k; i < len - 1; i++)
    {
        if (i < j)
            Swap(y[i],y[j]);
        k = len >> 1;
        while (j >= k)
        {
            j -= k;
            k >>= 1;
        }
        if (j < k)
            j += k;
    }
}

void FFT(node *y,ll op)
{
    zhuan(y);
    for (ll h = 2; h <= len; h <<= 1)
    {
        node temp(cos(op * pai * 2 / h),sin(op * pai * 2 / h));
        for (ll i = 0; i < len; i += h)
        {
            node W(1,0);
            for (ll j = i; j < i + h / 2; j++)
            {
                node u = y[j];
                node v = W * y[j + h / 2];
                y[j] = u + v;
                y[j + h / 2] = u - v;
                W = W * temp;
            }
        }
    }
    if (op == -1)
        for (ll i = 0; i < len; i++)
            y[i].real /= len;
}

void solve(node *A,node *B)
{
    FFT(A,1);
    FFT(B,1);
    for (ll i = 0; i < len; i++)
        A[i] = A[i] * B[i];
    FFT(A,-1);
}

void pre()
{
    len = 1;
    while (len < (n << 1))
        len <<= 1;
    for (ll i = 0; i < n; i++)
        A[i].set(a[i],0),B[i].set(b[n - i - 1],0),A[i + n].set(a[i],0);
    for (ll i = n; i < len; i++)
        B[i].set();
    for (ll i = 2 * n; i < len; i++)
        A[i].set();
}

int main()
{
    scanf("%lld%lld",&n,&m);
    for (ll i = 0; i < n; i++)
    {
        scanf("%lld",&a[i]);
        sum1 += a[i];
        sum11 += a[i] * a[i];
    }
    for (ll i = 0; i < n; i++)
    {
        scanf("%lld",&b[i]);
        sum2 += b[i];
        sum22 += b[i] * b[i];
    }
    pos1 = floor((double)(sum1 - sum2) / -n),pos2 = ceil((double)(sum1 - sum2) / -n);
    ans = min(pos1 * pos1 * n + 2 * (sum1 - sum2) * pos1,pos2 * pos2 * n + 2 * (sum1 - sum2) * pos2);
    ans += sum11 + sum22;
    pre();
    solve(A,B);
    ll temp = -inf;
    for (ll i = n - 1; i < 2 * n - 1; i++)
    {
        ll tmp = (ll)(A[i].real + 0.5);
        temp = max(temp,tmp);
    }
    ans -= temp * 2;
    printf("%lld\n",ans);

    return 0;
}