网络流练习题 比特板

分析：个人感觉非常神的一道题.

　　　类似于匹配问题，很容易看出这道题要用网络流来做. 

　　　观察特征：2^n个点，有2^m个位置可以选择，每种放法都有其相应的代价，求最大代价. 这是一类很经典的网络流问题. 思考的方向有两个：

　　　1.将位置看成点，向原图中的点连边就相当于一种选择. 将容量设为1来使得每个点只选择一个位置.

　　　2.拆点. 每个点拆成2^m个.分别表示选第j个位置. 

　　　如果用第一种方法，那就是最大流模型了，第二种方法就是最小割模型.

　　　第一种方法看上去很直观，但是只能计算对应位置和点之间的代价. 本题中涉及到不同比特元之间的代价，肯定不能用第一种方法，那么只好用第二种方法了.

　　　直接计算至少一个达到饱和值的比较难，反向思考：计算都小于饱和值的，最后用总答案减去最小割即可.

　　　脑补一下建图，大概是这样的：

　　　　

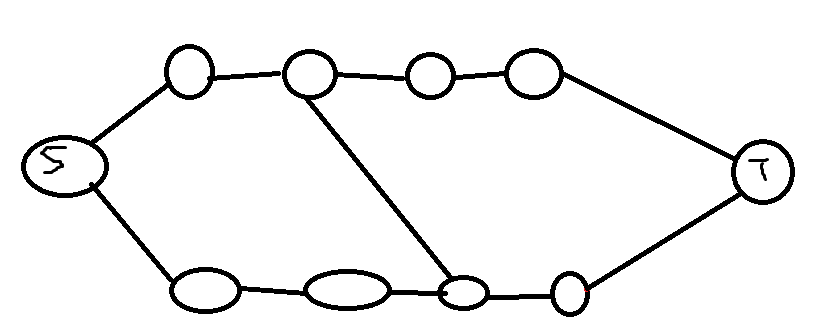
　　　　考虑三个问题：1.为什么要分奇偶讨论？

　　　2.为什么有奇数个1的时候连的边的容量是反着的？

　　　3.为什么最后考虑满足条件的a和b时，只考虑有奇数个1的？并且为什么连的是2^m - ta ---> tb?

　　　a和b在二进制下只有1位不同，意味着a和b之中有一个有偶数个1，有一个有奇数个1.不仅如此，还要从最小割的性质来考虑：

　　　

　　　　　考虑割掉红色的边，则必然会割掉中间这条有向边. 而且仅有这一种情况会割掉有向边（割掉的一条边在有向边右侧，一条在其左侧）. 这是反着连边和分奇偶讨论的图. 如果不反着连边，就会使得割的两条边在有向边的同一侧，这条有向边不能被割掉. 如果不分奇偶讨论，统计的答案可能会变多（割四条边+中间的这条边，暂且不称它为有向边），因为分奇偶讨论实际上是给边定了方向（有向边）.

　　　　使边的容量变反，奇偶讨论都是为了使得最小割与要求的答案相吻合.

　　　　解出这道题的关键就是两步转化：拆点和补集转化. 转化后构造方案使得最小割和要求的答案相吻合即可. 

　　　　坑点：W(i,j)可能是负数，不能直接求最小割. 一个方法是将W(i,j)变成x - W(i,j). x是一个常数. 那么一开始ans = 2^n * x. 最终的答案就是ans - 最小割.

 

#include <cstdio>
#include <queue>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 100010,inf = 0x7fffffff,maxm = 2000010;
int n,m,S,T,t[maxn],p[maxn],W[1010][1010],id[1010][1010],cnt;
int d[maxn];
int ans,head[maxn],to[maxm],nextt[maxm],w[maxm],tot = 2;

void add(int x,int y,int z)
{
    w[tot] = z;
    to[tot] = y;
    nextt[tot] = head[x];
    head[x] = tot++;

    w[tot] = 0;
    to[tot] = x;
    nextt[tot] = head[y];
    head[y] = tot++;
}

int get(int x)
{
    int res = 0;
    while (x)
    {
        if (x & 1)
            res++;
        x >>= 1;
    }
    return res;
}

bool bfs()
{
    memset(d,-1,sizeof(d));
    d[S] = 0;
    queue <int> q;
    q.push(S);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        if (u == T)
            return true;
        for (int i = head[u];i;i = nextt[i])
        {
            int v = to[i];
            if (w[i] && d[v] == -1)
            {
                d[v] = d[u] + 1;
                q.push(v);
            }
        }
    }
    return false;
}

int dfs(int u,int f)
{
    if (u == T)
        return f;
    int res = 0;
    for (int i = head[u];i;i = nextt[i])
    {
        int v = to[i];
        if (w[i] && d[v] == d[u] + 1)
        {
            int temp = dfs(v,min(f - res,w[i]));
            w[i] -= temp;
            w[i ^ 1] += temp;
            res += temp;
            if (res == f)
                return res;
        }
    }
    if (!res)
        d[u] = -1;
    return res;
}

void dinic()
{
    while (bfs())
        ans -= dfs(S,inf);
}

int main()
{
    scanf("%d%d",&n,&m);
    for (int i = 0; i < (1 << n); i++)
        scanf("%d",&t[i]);
    for (int i = 0; i < (1 << n); i++)
        scanf("%d",&p[i]);
    for (int i = 0; i < (1 << n); i++)
        for (int j = 0; j < (1 << m); j++)
            scanf("%d",&W[i][j]);
    for (int i = 0; i < (1 << n); i++)
        for (int j = 0; j <= (1 << m); j++)
            id[i][j] = ++cnt;
    S = ++cnt;
    T = ++cnt;
    ans = 3000 * (1 << n);
    for (int i = 0; i < (1 << n); i++)
    {
        add(S,id[i][0],inf);
        add(id[i][1 << m],T,inf);
        int temp = get(i);
        for (int j = 0; j < (1 << m); j++)
        {
            int val;
            if (temp % 2 == 1)
                val = W[i][(1 << m) - j - 1];
            else
                val = W[i][j];
            add(id[i][j],id[i][j + 1],3000 - val);
        }
        for (int j = 0; j < n; j++)
        {
            int x = i ^ (1 << j);
            if (temp % 2 == 1)
            {
                add(id[i][(1 << m) - t[i]],id[x][t[x]],p[i] ^ p[x]);
                ans += (p[i] ^ p[x]);
            }
        }
    }
    dinic();
    printf("%d\n",ans);

    return 0;
}