网络流的一类经典问题--二元费用问题

一、问题引入

　　有n个点，选和不选各自有收益。有m个条件，有三种：
如果x和y都选了，获得w的收益；
如果x和y都没选，获得w的收益；
如果x和y都一个选了一个没选，付出w的代价。
求最大收益。（n≤10000,m≤ 10）

二、分析

　　第一眼看上去很像2-sat?2-sat是对每一组变量都有限制，这道题并没有限制，不能用2-sat的做法.  

　　求最值，dp可以吗？ dp的话还要记录每个点的信息，也就是要状态压缩，这明显不能状压......

　　那要怎么做？正解比较难想到--网络流最小割！

　　类似于最大权闭合子图的建图方式，对于每一对有条件的x,y,可以建出如下子图：

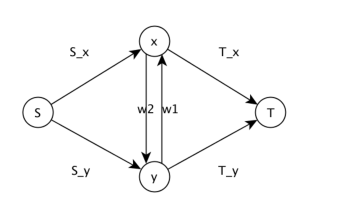　　,边权S_x,T_x,S_y,T_y,w1,w2暂时是不知道的.

　　考虑最小割的意义：

　　1.x和y都选。此时被割的边为S_x + S_y 。
　　2.x和y都没选。此时被割的边为T_x + T_y 。
　　3.x选y没选。此时被割的边为S_x + T_y + w1。
　　4.x没选y选。此时被割的边为T_x + S_y + w2。

　　为什么是这样的呢？假定割掉与源相连的边为选择这个点，割掉与汇相连的边为不选择这个点. 看第三种情况，为什么要割掉w1呢？因为最小割要使得S,T不连通. 如果不割掉w1,流就会从S到y到x到T，这是不合法的.

　　为了知道这些边权具体是多少，需要根据题目所给的信息来列方程：

　　设选x的收益为VAx ，不选的是VBx ，x和y都选的收益为EA，都不选的收益为EB，一选一不选的代价为EC。

　　由于被割的边是损失的代价，可以列出方程：

　　

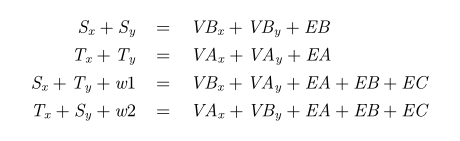
　　未知数比方程数要多，解不出来.  但是可以猜！

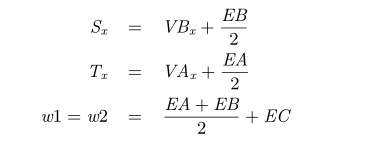　　可以带进式子中验证.

　　　像最大权闭合子图那样，最后的答案就是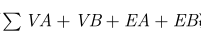减去最小割.

　　　具体实现上，因为对于每一个条件，x,y与源汇连边的边权是不同的，所以要对每一个点建m个点.

三、深入思考

　　为什么要加w1,w2这两条边呢？如果不加这两条边，方程是无解的！会凭空多出来一个EC.这是由数学反推回来的.

四、总结

　　这道题加深了我对最大权闭合子图的理解. 最大权闭合子图可以看作是把若干个点捆绑在一起. 选择的方式不同收益/代价也就不同，通过最小割来求最优解.

　　每一条割边都有实际意义！例如割sx就代表选x,割tx就代表不选y,求出来的最小割一定是使得源点和汇点不连通的！所以考虑割边的时候要考虑是否是合法的！

　　每一条割边都会有贡献，但是捆绑在一起贡献就不确定了，通过解方程来确定. 发现方程无解通过加边来调整，改变每一种情况割边的方案,同时一定要保证源点和汇点不连通！