bzoj3669 [Noi2014]魔法森林
3669: [Noi2014]魔法森林
Time Limit: 30 Sec Memory Limit: 512 MBSubmit: 3287 Solved: 2100
[Submit][Status][Discuss]
Description
为了得到书法大家的真传，小E同学下定决心去拜访住在魔法森林中的隐士。魔法森林可以被看成一个包含个N节点M条边的无向图，节点标号为1..N，边标号为1..M。初始时小E同学在号节点1，隐士则住在号节点N。小E需要通过这一片魔法森林，才能够拜访到隐士。
魔法森林中居住了一些妖怪。每当有人经过一条边的时候，这条边上的妖怪就会对其发起攻击。幸运的是，在号节点住着两种守护精灵：A型守护精灵与B型守护精灵。小E可以借助它们的力量，达到自己的目的。
只要小E带上足够多的守护精灵，妖怪们就不会发起攻击了。具体来说，无向图中的每一条边Ei包含两个权值Ai与Bi。若身上携带的A型守护精灵个数不少于Ai，且B型守护精灵个数不少于Bi，这条边上的妖怪就不会对通过这条边的人发起攻击。当且仅当通过这片魔法森林的过程中没有任意一条边的妖怪向小E发起攻击，他才能成功找到隐士。
由于携带守护精灵是一件非常麻烦的事，小E想要知道，要能够成功拜访到隐士，最少需要携带守护精灵的总个数。守护精灵的总个数为A型守护精灵的个数与B型守护精灵的个数之和。
Input
第1行包含两个整数N,M，表示无向图共有N个节点，M条边。 接下来M行，第行包含4个正整数Xi,Yi,Ai,Bi，描述第i条无向边。其中Xi与Yi为该边两个端点的标号，Ai与Bi的含义如题所述。 注意数据中可能包含重边与自环。
Output
输出一行一个整数：如果小E可以成功拜访到隐士，输出小E最少需要携带的守护精灵的总个数；如果无论如何小E都无法拜访到隐士，输出“-1”（不含引号）。
Sample Input
4 5
1 2 19 1
2 3 8 12
2 4 12 15
1 3 17 8
3 4 1 17
【输入样例2】
3 1
1 2 1 1
Sample Output
32
【样例说明1】
如果小E走路径1→2→4，需要携带19+15=34个守护精灵；
如果小E走路径1→3→4，需要携带17+17=34个守护精灵；
如果小E走路径1→2→3→4，需要携带19+17=36个守护精灵；
如果小E走路径1→3→2→4，需要携带17+15=32个守护精灵。
综上所述，小E最少需要携带32个守护精灵。
【输出样例2】
-1
【样例说明2】
小E无法从1号节点到达3号节点，故输出-1。
HINT
2<=n<=50,000
0<=m<=100,000
1<=ai ,bi<=50,000
分析：很好的一道题！
两个量ai,bi影响答案，一个非常常见的做法就是对每条边以ai为关键字从小到大排序，这样从1到m枚举每条边，那么当前枚举到的ai就是最大的a了. 只需要使得路径上最大的b最小就好了.
这道题的目的是使得1,n连通，并且1,n路径上最大的a加上最大的b的和最小. 当前已经知道了最大的a是多少，剩下的就是使得1,n连通并且让最大的b最小.
维护无向图的连通性可以用并查集.
考虑第i条边的时候，如果这条边连接的两个点没有连通，直接加上这条边就好了.
如果连通了，则找到这两个点链上的最大的b,如果第i条边的b比这个最大的b要小，那么第i条边肯定要优，删掉那条拥有最大的b的边，加入第i条边.
这个删边的方法是最小生成树问题上一个比较常用的方法，具体可见：传送门.
怎么支持加边删边？ LCT！
LCT只能维护点权，这道题要维护边权怎么办啊？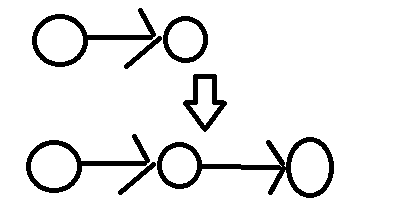 
例如这张图，上面的表示原来的边(x,y). 在x,y中间插入一个点k. k点的点权就是(x,y)的b. 每次加边先加(x,k)，再加(k,y),删边是类似的.
需要注意的是：加入的点序号不能与原splay中的点重复，也就是说：如果这个点属于第i条边，那么这个点的编号就是i+n. 删边和加边的时候要注意!
Get到了LCT的新套路，想到对ai排序后就没往连通性那方面去想了，经验不足啊. 其实遇到这类2个因素影响答案的问题，就应该往两个方面去想：1.对其中一个进行排序，消除影响,例如：传送门. 2.变成二元组放在平面直角坐标系上，看看有没有什么性质能够对其进行优化,例如：bzoj1597.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int maxn = 200010,inf = 0x7ffffff; int n,m,f[maxn],val[maxn],ans = inf,sta[maxn]; int fa[maxn],son[maxn][2],maxx[maxn],rev[maxn]; struct node { int x,y,a,b; }e[maxn]; bool cmp(node p,node q) { if (p.a == q.a) return p.b < q.b; return p.a < q.a; } bool is_root(int x) { return son[fa[x]][0] != x && son[fa[x]][1] != x; } bool get(int x) { return son[fa[x]][1] == x; } int find(int x) { if (x == f[x]) return x; return f[x] = find(f[x]); } int pushdown(int x) { if (rev[x]) { rev[son[x][0]] ^= 1; rev[son[x][1]] ^= 1; rev[x] = 0; swap(son[x][0],son[x][1]); } } void pushup(int x) { maxx[x] = x; if (son[x][0]) if (val[maxx[son[x][0]]] > val[maxx[x]]) maxx[x] = maxx[son[x][0]]; if (son[x][1]) if (val[maxx[son[x][1]]] > val[maxx[x]]) maxx[x] = maxx[son[x][1]]; } void turn(int x) { int y = fa[x]; int z = fa[y]; int temp = get(x); if (!is_root(y)) son[z][son[z][1] == y] = x; fa[x] = z; son[y][temp] = son[x][temp ^ 1]; fa[son[y][temp]] = y; son[x][temp ^ 1] = y; fa[y] = x; pushup(y); pushup(x); } void splay(int x) { int top = 0; sta[++top] = x; for (int y = x; !is_root(y); y = fa[y]) sta[++top] = fa[y]; for (int i = top; i >= 1; i--) pushdown(sta[i]); int temp; for (; !is_root(x); turn(x)) { if (!is_root(temp = fa[x])) { if (get(x) == get(temp)) turn(temp); else turn(x); } } } void Access(int x) { int p = 0; for (; x; p = x,x = fa[x]) { splay(x); son[x][1] = p; pushup(x); //注意pushup } } void Reverse(int x) { Access(x); splay(x); rev[x] ^= 1; } void Cut(int x,int y) { Reverse(x); Access(y); splay(y); son[y][0] = fa[x] = 0; } void Link(int x,int y) { Reverse(x); fa[x] = y; splay(x); } int query(int x,int y) { Reverse(x); Access(y); splay(y); return maxx[y]; } int main() { scanf("%d%d",&n,&m); for (int i = 1; i <= m; i++) scanf("%d%d%d%d",&e[i].x,&e[i].y,&e[i].a,&e[i].b); sort(e + 1,e + 1 + m,cmp); for (int i = 1; i <= n; i++) f[i] = i; for (int i = 1; i <= m; i++) val[i + n] = e[i].b; for (int i = 1; i <= m; i++) { int x = e[i].x,y = e[i].y; int fx = find(x),fy = find(y); if (fx != fy) { f[fx] = fy; Link(x,i + n); Link(i + n,y); } else { int k = query(x,y); if (val[k] > e[i].b) { Cut(e[k - n].x,k); Cut(k,e[k - n].y); Link(x,i + n); Link(i + n,y); } } if (find(1) == find(n)) ans = min(ans,e[i].a + val[query(1,n)]); } if (ans == inf) printf("%d\n",-1); else printf("%d\n",ans); return 0; }
